Download Item VIII

Supplement
– Statistical Thermodynamics
고려대학교 화공생명공학과
강정원
Contents
1. Introduction
2. Distribution of Molecular States
3. Interacting Systems – Gibbs Ensemble
4. Classical Statistical Mechanics
1. Introduction
 Mechanics : Study of position, velocity, force and
energy
 Classical Mechanics (Molecular Mechanics)
• Molecules (or molecular segments) are treated as rigid object
(point, sphere, cube,...)
• Newton’s law of motion
 Quantum Mechanics
• Molecules are composed of electrons, nuclei, ...
• Schrodinger’s equation  Wave function
1. Introduction

Methodology of Thermodynamics and Statistical Mechanics
 Thermodynamics
• study of the relationships between macroscopic properties
–

Statistical Mechanics (Statistical Thermodynamics)
•
how the various macroscopic properties arise as a consequence of the microscopic nature of
the system
–

Volume, pressure, compressibility, …
Position and momenta of individual molecules (mechanical variables)
Statistical Thermodynamics (or Statistical Mechanics) is a link between microscopic
properties and bulk (macroscopic) properties
Thermodynamic Variables
Pure mechanical variables
Statistical
Mechanics
Methods of QM
Methods of MM
U
A particular
microscopic model
can be used
r
P
T
V
1.Introduction
 Equilibrium Macroscopic Properties
 Properties are consequence of average of individual
molecules
 Properties are invariant with time  Time average
Mechanical
Properties of
Individual
Molecules
position, velocity
energy, ...
average
over molecules
2
average
over time
3
statistical
thermodynamics
4
Thermodynamic
Properties
temperature, pressure
internal energy, enthalpy,...
1. Introduction
 Description of States
 Macrostates : T, P, V, … (fewer variables)
 Microstates : position, momentum of each particles (~1023 variables)
 Fundamental methodology of statistical mechanics
 Probabilistic approach : statistical average
• Most probable value
 Is it reasonable ?
• As N approaches very large number, then fluctuations are negligible
• “Central Limit Theorem” (from statistics)
• Deviation ~1/N0.5
2. Distribution of Molecular States
 Statistical Distribution
 n : number of occurrences
 b : a property
if we know “distribution”
we can calculate the average
value of the property b
ni
b
1 2 3 4 5 6
2. Distribution of Molecular States
 Normalized Distribution Function
 Probability Distribution Function
Pi (bi ) 
ni (bi )
n (b )
 i i
n
 ni (bi )
i
 P (b )  1
i
i
i
Pi
 b   bi Pi
i
b1 b2 b3 b4 b5 b6
b
 F (b)   F (bi ) Pi
i
Finding probability (distribution) function is
the main task in statistical thermodynamics
2. Distribution of Molecular States
 Quantum theory says ,
 Each molecules can have only discrete values of energies
 Evidence





Black-body radiation
Planck distribution
Heat capacities
Atomic and molecular spectra
Wave-Particle duality
Energy
Levels
2. Distribution of Molecular States
 Configuration ....
 At any instance, there may be no molecules at e0 , n1
molecules at e1 , n2 molecules at e2 , …
 {n0 , n1 , n2 …} configuration
e
5
e4
e3
e2
e
1e
0
{ 3,2,2,1,0,0}
2. Distribution of Molecular States
 Weight ....
 Each configurations can be achieved in different ways
 Example1 : {3,0} configuration  1
e
1e
0
 Example2 : {2,1} configuration  3
e
1e
e
1e
e
1e
0
0
0
2. Distribution of Molecular States
 Calculation of Weight ....
 Weight (W) : number of ways that a configuration can be achieved in
different ways
 General formula for the weight of {n0 , n1 , n2 …} configuration
N!
N!
W

n1!n2 !n3!...  ni !
Example1
{1,0,3,5,10,1} of 20 objects
W = 9.31E8
i
Example 2
{0,1,5,0,8,0,3,2,1} of 20 objects
W = 4.19 E10
Principles of Equal a Priori Probability
 All distributions of energy are equally probable
 If E = 5 and N = 5 then
5
5
5
4
3
2
1
0
4
3
2
1
0
4
3
2
1
0
All configurations have equal probability, but
possible number of way (weight) is different.
A Dominating Configuration
 For large number of molecules and large number of energy
levels, there is a dominating configuration.
 The weight of the dominating configuration is much more
larger than the other configurations.
Wi
Configurations
{ni}
Dominating Configuration
W = 1 (5!/5!)
5
5
5
4
3
2
1
0
4
3
2
1
0
4
3
2
1
0
W = 20 (5!/3!)
W = 5 (5!/4!)
Difference in W becomes larger when N is increased !
In molecular systems (N~1023) considering the
most dominant configuration is enough for average
How to find most dominant
configuration ?
 The Boltzmann Distribution
 Task : Find the dominant configuration for given N and
total energy E
 Method : Find maximum value of W which satisfies,
N   ni
i
E   e i ni
i
 dn
i
0
i
 e dn
i
i
i
0
Stirling's approximation
 A useful formula when dealing with factorials of
large numbers.
ln N! N ln N  N
N!
ln W  ln
 ln N ! ln ni !
n1!n2 !n3!...
i
 N ln N  N   ni ln ni   ni
i
 N ln N   ni ln ni
i
i
Method of Undetermined
Multipliers
 Maximum weight , W
Recall the method to find min, max of a function…
d ln W  0
  ln W 

  0
 dni 
 Method of undetermined multiplier :
 Constraints should be multiplied by a constant and
added to the main variation equation.
Method of Undetermined
Multipliers
undetermined multipliers
  ln W 
dni    dni    e i dni
d ln W   
i  dni 
i
i
  ln W 

    ei dni  0
  
i  dni 

  ln W 

    ei  0
 dni 
Method of Undetermined
Multipliers
ln W  N ln N   ni ln ni
  ln W

 ni
 (n j ln n j )
 N ln N
 

ni
ni
j

N ln N  N 
1  N 
 ln N  N  
  ln N  1
 
ni
N  ni 
 ni 

j
 (n j ln n j )
ni
 n j 
1
 ln n j  n j 
  
nj
j 
 ni 
n
 ln W
 (ln ni  1)  (ln N  1)   ln i
ni
N
 n j 

  ln ni  1
 ni 
Method of Undetermined
Multipliers
 ln
ni
   ei  0
N
ni
 e  e i
N
Normalization Condition
N   n j  Ne  e
j
e 
 e j
j
1
 e
e j
j
ni
e  e i
Pi  
N  e  e j
j
Boltzmann Distribution
(Probability function for
energy distribution)
The Molecular Partition Function
 Boltzmann Distribution
ni
e  e i
e  e i
pi  

 e j
N e
q
j
 Molecular Partition Function
q  e
 e j
j
 Degeneracies : Same energy value but different states (gjfold degenerate)
q
 g je
levels
j
 e j
How to obtain the value of beta ?
 Assumption :
  1 / kT
 T 0 then q  1
 T infinity then q  infinity
 The molecular partition function gives an indication of the
average number of states that are thermally accessible to a
molecule at T.
2. Interacting Systems
– Gibbs Ensemble
 Solution to Schrodinger equation (Eigen-value problem)
 Wave function
 Allowed energy levels : En
h2
  2  i2   U  E
i 8 mi
 Using the molecular partition function, we can calculate
average values of property at given QUANTUM STATE.
 Quantum states are changing so rapidly that the observed
dynamic properties are actually time average over quantum
states.
Fluctuation with Time
states
time
Although we know most probable distribution of energies of individual
molecules at given N and E (previous section – molecular partition
function) it is almost impossible to get time average for interacting
molecules
Thermodynamic Properties
 Entire set of possible quantum states
1 , 1 , 1 ,...i ,...
E1 , E2 , E3 ,..., Ei ,...
 Thermodynamic internal energy
U  lim
 
1
E t


i
i
i
Difficulties
 Fluctuations are very small
 Fluctuations occur too rapidly
We have to use alternative, abstract approach.
Ensemble average method (proposed by Gibbs)
Alternative Procedure
 Canonical Ensemble
 Proposed by J. W. Gibbs (1839-1903)
 Alternative procedure to obtain average
 Ensemble : Infinite number of mental replica
of system of interest
Large reservoir (constant T)
All the ensemble members have the same (n, V, T)
Energy can be exchanged but
particles cannot
Number of Systems : N
N∞
Two Postulate
Fist Postulate
The long time average of a mechanical variable M is
equal to the ensemble average in the limit N ∞
time
E1
E2
E3
E4
E5
Second Postulate (Ergodic Hypothesis)
The systems of ensemble are distributed uniformly for (n,V,T) system
Single isolated system spend equal amount of time
Averaging Method
 Probability of observing particular quantum state i
n~i
Pi 
 n~i
i
 Ensemble average of a dynamic property
 E   Ei Pi
i
 Time average and ensemble average
U  lim  Ei ti  lim
 
n 
E P
i i
i
How to find Most Probable
Distribution ?
 Calculation of Probability in an Ensemble
 Weight
~
~
N!
N!
W ~ ~ ~

n1!n2 !n3!...  n~i !
i
 Most probable distribution = configuration with maximum weight
 Task : find the dominating configuration for given N and E
• Find maximum W which satisfies
~
N   n~i
i
Et   Ei n~i
i
~ 0
d
n
 i
i
~ 0
E
d
n
 i i
i
Canonical Partition Function
 Similar method (Section 2) can be used to get most
probable distribution
ni
e  Ei
Pi  
N  e  E j
j
ni
e  Ei
e  Ei
Pi  

 E j
N e
Q
j
Q  e
j
 E j
Canonical Partition Function
How to obtain beta ?
– Another interpretation
dU  d ( Ei Pi )   Ei dPi  Pi dEi
i
i
i
dU  qrev  wrev  TdS  pdV
 Ei 
 P dE   P  V 
i
i
i
i
 Ei dPi  
i
dV   PdV  wrev
i
1

N
( ln Pi dPi  ln Q  dPi )  
i
i
1

 ln P dP  TdS  dq
i
i
i
The only function that links heat (path integral) and
state property is TEMPERATURE.
  1 / kT
rev
Properties from Canonical Partition
Function
 Internal Energy
U  E   Ei Pi 
i
1
 Ei
E
e
 i
Q i ( qs)
 Q 

    Ei e  Ei
i ( qs )
   N ,V
  ln Q 
1  Q 
  

U   
Q    N ,V



 N ,V
Properties from Canonical Partition
Function
 Pressure
(wi ) N  Pi dV  Fi dx
Small Adiabatic expansion of system
(dEi ) N   Fi dx   Pi dV  wi
dx
 E 
Pi   i 
 V  N
P  P   Pi Pi
Fi
dV
V
i
P
1
1
 Ei   Ei
 Ei
P
e


 e


i
Q i
Q i  V  N
  E 
  ln Q 
   i  e  Ei


 V   , N Q i  V  N
P
1   ln Q 


  ln V 
dEi
Ei
Thermodynamic Properties from
Canonical Partition Function
 ln Q
)V , N
 ln T
 ln Q


S  k  ln Q  (
)V , N 
 ln T


U  kT (
 ln Q
  ln Q

H  kT  (
)V , N  (
)T , N 
 ln V
  ln T

A  kT ln Q
 ln Q


G  kT  ln Q  (
)T , N 
 ln V


  ln Q 

 i  kT 
 N i T ,V , N
j i
Grand Canonical Ensemble
 Ensemble approach for open system
 Useful for open systems and mixtures
 Walls are replaced by permeable walls
Large reservoir (constant T )
All the ensemble members have the same (V, T, i )
Energy and particles can be exchanged
Number of Systems : N
N∞
Grand Canonical Ensemble
 Similar approach as Canonical Ensemble
 We cannot use second postulate because systems are not isolated
 After equilibrium is reached, we place walls around ensemble and treat
each members the same method used in canonical ensemble
After
equilibrium
T,V,
T,V,N1
T,V,N3
T,V,N2
Each members are (T,V,N) systems
 Apply canonical ensemble methods for each member
T,V,N5
T,V,N4
Grand Canonical Ensemble
 Weight and Constraint


 n j ( N )!
j,N


W
 n j ( N )!
Number of ensemble members
N   n j (N )
Number of molecules after
fixed wall has been placed
j,N
Et   n j ( N ) E j (V , N )
j,N
j,N
Nt   n j ( N ) N
Method of undetermined multiplier
with ,  ,g
n*j ( N )  Ne  e
Pj ( N ) 
j,N
 E j ( N ,V ) gN
n j (N )
N
e

n*j ( N )
N

e
 E j ( N ,V )  gN
e
j,N
e
 E j ( N ,V ) gN
e
Grand Canonical Ensemble
 Determination of Undetermined Multipliers
U  E   Pj ( N ) E j ( N ,V )
  e
j,N
dU   E j ( N ,V )dPj ( N )   Pj ( N )dE j ( N ,V )
j,N
dU  
 E j ( N ,V ) gN
j,N
j,N
E ( N ,V )


g
N

ln
P
(
N
)

ln

dP
(
N
)

P
(
N
)
dV



V
1
j
j
j
j
j,N
j,N
dU  TdS  pdV  dN
Comparing two equation gives,

  e
j,N
 E j ( N ,V ) / kT
e
N / kT
1
kT
g 

kT
Grand Canonical Partition Function
e
4. Classical Statistical Mechanics
 The formalism of statistical mechanics relies very much at the
microscopic states.
 Number of states , sum over states
 convenient for the framework of quantum mechanics

What about “Classical Sates” ?
 Classical states
• We know position and velocity of all particles in the system
 Comparison between Quantum Mechanics and Classical Mechanics
QM Problem
H  E 
Finding probability and discrete energy states
CM Problem
F  ma
Finding position and momentum of individual molecules
Newton’s Law of Motion
 Three formulations for Newton’s second law of motion
 Newtonian formulation
 Lagrangian formulation
 Hamiltonian formulation
H (r N , p N )  KE(kinetic energy)  PE(potenti al energy)
p
H (r N , p N )   i U (r1 , r2 ,..., rN )
i 2mi
 H 

  p i
 ri 
 H 

  ri
 p i 
ri p i

t mi
r  r (rx , ry , rz )
p i
 Fi
t
Fi   Fij
p  p( p x , p y , p z )
j 1
j i
Classical Statistical Mechanics
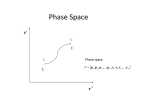
 Instead of taking replica of systems, use abstract “phase space”
composed of momentum space and position space (total 6N-space)
pN
t2
2
t1
1
Phase space
  p1 , p 2 , p3 ,..., p N , r1 , r1 , r3 ,..., rN 
rN
Classical Statistical Mechanics
 “ Classical State “ : defines a cell in the space (small volume of
momentum and positions)
" Classical State"  dqx dq y dqz drx dry drz  d 3 pd 3r for simplicity
 Ensemble Average
U  lim
 
1


0
E ()d  lim  P N () E ()d
PN ()d
n 
Fraction of Ensemble members in this range
( to +d)
Using similar technique used for
Boltzmann distribution
PN ()d 
exp(  H / kT )d
 ... exp( H / kT )d
Classical Statistical Mechanics
 Canonical Partition Function
Phase Integral
T   ... exp(  H / kT )d
Canonical Partition Function
Q  c  ... exp(  H / kT )d
Match between Quantum
and Classical Mechanics
c  lim
T 
 exp(  E / kT )
i
i
 ... exp(  H / kT )d
1
N!h NF
For rigorous derivation see Hill, Chap.6 (“Statistical Thermodynamics”)
c
Classical Statistical Mechanics
 Canonical Partition Function in Classical Mechanics
1
Q 
... exp( H / kT )d
NF  
N !h
Example ) Translational Motion for
Ideal Gas
H (r N , p N )  KE(kinetic energy)  PE(potenti al energy)
H (r N , p N )  
i
3N
H 
i
pi
U (r1 , r2 ,..., rN )
2mi
No potential energy, 3 dimensional
space.
2
pi
2mi
pi2
1
Q
... exp( 
)dp1...dp N dr1...drN
3N  
N !h
i 2mi

1
N !h 3 N
3N

 V

p
)dp    dr1dr2 dr3 
  exp( 
2mi
 
 0

1  2mkT 

N !  h 2 
N
3N / 2
VN
We will get ideal gas law
pV= nRT
Semi-Classical Partition Function

The energy of a molecule is distributed in different modes
 Vibration, Rotation (Internal : depends only on T)
 Translation (External : depends on T and V)

Assumption 1 : Partition Function (thus energy distribution) can be separated
into two parts (internal + center of mass motion)
EiCM  Eiint
EiCM
Eiint
Q   exp( 
)   exp( 
) exp( 
)
kT
kT
kT
Q  QCM ( N ,V , T )Qint ( N , T )
Semi-Classical Partition Function
 Internal parts are density independent and most of the
components have the same value with ideal gases.
Qint ( N ,  , T )  Qint ( N ,0, T )
 For solids and polymeric molecules, this assumption is not
valid any more.
Semi-Classical Partition Function
 Assumption 2 : for T>50 K , classical approximation can be
used for translational motion
H CM  
pix2  piy2  piz2
2m
i
 U (r1 , r2 ,..., r3 N )
pix2  piy2  piz2
1
Q
... exp( 
)dp 3 N  ... (U / kT )dr 3 N
3N  
N!h
2mkT
i
3 N

Z
N!
Configurational Integral
1/ 2
 h2 

  
 2mkT 
Z   ... (U / kT )dr1dr2 ...dr3 N
Q
1
Qint 3 N Z
N!
Another, Different Treatment
Statistical Thermodynamics:
the basics
•
•
Nature is quantum-mechanical
Consequence:
–
–
•
•
Systems have discrete quantum states.
For finite “closed” systems, the number of
states is finite (but usually very large)
Hypothesis: In a closed system, every
state is equally likely to be observed.
Consequence: ALL of equilibrium
Statistical Mechanics and
Thermodynamics
Each individual
microstate is
equally probable
…, but there are not
many microstates that
give these extreme
results
Basic assumption
If the number of
particles is large (>10)
these functions are
sharply peaked
Does the basis assumption lead to something
that is consistent with classical
thermodynamics?
E1
E2  E  E1
Systems 1 and 2 are weakly coupled
such that they can exchange energy.
What will be E1?
W  E1 , E  E1   W1  E1  W2  E  E1 
BA: each configuration is equally probable; but the number of
states that give an energy E1 is not know.
W  E1 , E  E1   W1  E1  W2  E  E1 
ln W  E1 , E  E1   ln W1  E1   ln W2  E  E1 
  ln W  E1 , E  E1  
0


E1

 N1 ,V1
 

Energy is conserved!
dE1=-dE2

 lnW1 E1 
 lnW2 E  E1 




E1
E1

 N ,V 
N
1
1
0
2 ,V2
  ln W1  E1  
  ln W2  E  E1  




E1
E2

 N1 ,V1 
 N2 ,V2
  ln W  E  
 

E

 N ,V
1   2
This can be seen as an
equilibrium condition
Entropy and number of
configurations
Conjecture:
S  ln W
Almost right.
•Good features:
•Extensivity
•Third law of thermodynamics comes for free
•Bad feature:
•It assumes that entropy is dimensionless but (for
unfortunate, historical reasons, it is not…)
We have to live with the past, therefore
S  kB ln W  E 
With kB= 1.380662 10-23 J/K
In thermodynamics, the absolute (Kelvin)
temperature scale was defined such that
1
 S 

 
 E  N ,V T
n
dE  TdS-pdV   idNi
i 1
But we found (defined):
  ln W  E  
 

E

 N ,V
And this gives the “statistical” definition of temperature:
  ln W  E  
1
 kB 

T
E

 N ,V
In short:
Entropy and temperature are both related to
the fact that we can COUNT states.
Basic assumption:
1. leads to an equilibrium condition: equal temperatures
2. leads to a maximum of entropy
3. leads to the third law of thermodynamics
Number of configurations
How large is W?
•For macroscopic systems, super-astronomically large.
•For instance, for a glass of water at room temperature:
W  10
210
25
•Macroscopic deviations from the second law of
thermodynamics are not forbidden, but they are
extremely unlikely.
Canonical ensemble
1/kBT
Consider a small system that can exchange heat with a big reservoir
Ei
 ln W
ln W  E  Ei   ln W  E  
Ei 
E
E  Ei
ln
W  E  Ei 
WE
Hence, the probability to find Ei:
P  Ei  
W  E  Ei 

exp   Ei k BT 
 WE  E  
j
j
Ei

k BT
j
exp   E j k BT 
P  Ei   exp   Ei kBT 
Boltzmann distribution
Example: ideal gas
1
recall
Q  N ,V , T  Thermo

dr (3)exp   U  r  

 N!
N
N
3N
Helmholtz Free energy:N
1
V
 dF3 N  SdTdr p1dV 3 N
 N!
 N!
N
Free energy: Pressure
N


V
F 

 F   ln  3 N   P
 VT N ! 
N
3
Energy:
 N ln   N ln    N ln 3  N ln 
Pressure:
V 

  F 
F T 


E
 
  1 T   Energy:
N
 F 
P  
 
 V T V
  F  3N  3
E 
 Nk BT

     2
Ensembles
•
•
•
•
Micro-canonical ensemble: E,V,N
Canonical ensemble: T,V,N
Constant pressure ensemble: T,P,N
Grand-canonical ensemble: T,V,μ
Each individual
microstate is
equally probable
…, but there are not
many microstates that
give these extreme
results
Basic assumption
If the number of
particles is large (>10)
these functions are
sharply peaked
Does the basis assumption lead to something
that is consistent with classical
thermodynamics?
E1
E2  E  E1
Systems 1 and 2 are weakly coupled
such that they can exchange energy.
What will be E1?
W  E1 , E  E1   W1  E1  W2  E  E1 
BA: each configuration is equally probable; but the number of
states that give an energy E1 is not know.
W  E1 , E  E1   W1  E1  W2  E  E1 
ln W  E1 , E  E1   ln W1  E1   ln W2  E  E1 
  ln W  E1 , E  E1  
0


E1

 N1 ,V1
 

Energy is conserved!
dE1=-dE2

 lnW1 E1 
 lnW2 E  E1 




E1
E1

 N ,V 
N
1
1
0
2 ,V2
  ln W1  E1  
  ln W2  E  E1  




E1
E2

 N1 ,V1 
 N2 ,V2
  ln W  E  
 

E

 N ,V
1   2
This can be seen as an
equilibrium condition
Entropy and number of
configurations
Conjecture:
S  ln W
Almost right.
•Good features:
•Extensivity
•Third law of thermodynamics comes for free
•Bad feature:
•It assumes that entropy is dimensionless but (for
unfortunate, historical reasons, it is not…)
We have to live with the past, therefore
S  kB ln W  E 
With kB= 1.380662 10-23 J/K
In thermodynamics, the absolute (Kelvin)
temperature scale was defined such that
1
 S 

 
 E  N ,V T
n
dE  TdS-pdV   idNi
i 1
But we found (defined):
  ln W  E  
 

E

 N ,V
And this gives the “statistical” definition of temperature:
  ln W  E  
1
 kB 

T
E

 N ,V
In short:
Entropy and temperature are both related to
the fact that we can COUNT states.
Basic assumption:
1. leads to an equilibrium condition: equal temperatures
2. leads to a maximum of entropy
3. leads to the third law of thermodynamics
Number of configurations
How large is W?
•For macroscopic systems, super-astronomically large.
•For instance, for a glass of water at room temperature:
W  10
210
25
•Macroscopic deviations from the second law of
thermodynamics are not forbidden, but they are
extremely unlikely.
Canonical ensemble
1/kBT
Consider a small system that can exchange heat with a big reservoir
Ei
 ln W
ln W  E  Ei   ln W  E  
Ei 
E
E  Ei
ln
W  E  Ei 
WE
Hence, the probability to find Ei:
P  Ei  
W  E  Ei 

exp   Ei k BT 
 WE  E  
j
j
Ei

k BT
j
exp   E j k BT 
P  Ei   exp   Ei kBT 
Boltzmann distribution
Example: ideal gas
1
recall
Q  N ,V , T  Thermo

dr (3)exp   U  r  

 N!
N
N
3N
Helmholtz Free energy:N
1
V
 dF3 N  SdTdr p1dV 3 N
 N!
 N!
N
Free energy: Pressure
N


V
F 

 F   ln  3 N   P
 VT N ! 
N
3
Energy:
 N ln   N ln    N ln 3  N ln 
Pressure:
V 

  F 
F T 


E
 
  1 T   Energy:
N
 F 
P  
 
 V T V
  F  3N  3
E 
 Nk BT

     2
Ensembles
•
•
•
•
Micro-canonical ensemble: E,V,N
Canonical ensemble: T,V,N
Constant pressure ensemble: T,P,N
Grand-canonical ensemble: T,V,μ