* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Magnetism - Stevens Institute of Technology
History of electromagnetic theory wikipedia , lookup
Electrostatics wikipedia , lookup
Condensed matter physics wikipedia , lookup
Field (physics) wikipedia , lookup
Maxwell's equations wikipedia , lookup
Neutron magnetic moment wikipedia , lookup
Magnetic field wikipedia , lookup
Electromagnetism wikipedia , lookup
Magnetic monopole wikipedia , lookup
Aharonov–Bohm effect wikipedia , lookup
Superconductivity wikipedia , lookup
Magnetism
(Chapter 33)
(Hans Christian Oersted: Danish scientist who discovered
relationship between electricity and magnetism in 1820)
Brief History of Magnetism.
• Magnetism like electricity has been known for several thousand years
– First mention of static electricity and it s forces: ~600 B.C. by Thales
of Miletus (Greek). (Word for electron is from the Greek word for
amber.)
– According to Aristotle, the same Thales was the first to mention of
magnetism.
– In ancient China in the 4th century B.C., Book of the Devil Valley
Master (鬼谷子): "The lodestone makes iron come or it attracts it.
– The ancient Chinese scientist Shen Kuo (1031-1095 AD) was the first
person to write of the magnetic needle compass and that it improved
the accuracy of navigation.
– Alexander Neckham in 1187 was the first in Europe to describe the
compass and its use for navigation.
– In 1600, William Gilbert concludes that the Earth is itself a magnetic
and this explains compasses.
– In 1820, Hans Christian Oersted in Copenhagen discovered that
an electric current produces a magnetic field.
What Do We Already Know About Magnetism
From Childhood?
•
Magnetism is a long range force
•
Not all objects materials are attracted to a
magnet. Only certain metals (iron, cobalt,
nickel) are magnetic materials and
respond to a magnet.
•
Magnets have two poles, north (N) and
south (S). There is an attractive force
between opposite poles and repulsive force
between like poles.
•
A compass is a tiny magnet: N pole of a bar
magnet attracts one end of a compass while
S pole attracts other end.
The Magnetic Field
The magnetic field is defined similarly
to the electric field:
1. The magnetic field (B)exists at all points
in space surrounding a magnet (or current
carrying wire)
2. It is a vector field: At each point it has
both a magnitude and direction.
3. The magnetic field exerts forces on
magnetic poles:
• A N pole feels a force
in the direction (parallel) of the field.
• A S pole feels a force opposite
to the direction (anti-parallel) of the
field.
A compass needle can be
used to find the direction of
the magnetic field.
Superposition
• The magnetic field just like the electric field
obeys the principle of superposition.
• If one has N magnets, the total magnetic field
is the sum of the fields from each magnet
!
! !
!
!
Btotal = B1 + B2 + B3 + ... + BN
Magnetic Field of a Bar Magnet
The magnetic field lines
point away from the N pole
and towards the S pole.
The magnetic field of a bar
magnet looks just like the
E field of an electric dipole
Monopoles and Dipoles: What Happens When
You Cut a Magnet ?
If you cut a magnet into two pieces you get two smaller magnets
each of which has it s own N and S poles. You DO NOT get an
isolated N pole and S pole when you cut a magnet.
A magnet is a magnetic dipole.
Since a magnet and E-dipole have same fields, what if you cut an
E-dipole ?
THERE ARE NO MAGNETIC MONOPOLES !
There is no Coulomb s Law for Magnetism
Discovering the Link Between Electricity and
Magnetism
In 1820, Hans Christian Oersted noticed in the middle of class
that a wire with an electric current deflected a compass needle
Oersted discovered that magnetic fields are created by electric
currents !
Right hand rule!
Two Kinds of Magnetism ??
• Textbook is not exactly correct: There is one kind of magnetic
field but two ways to create a magnetic field
• All magnetic fields are created by one of two means:
– Electric currents
– Spin
• All fundamental particles (electron, proton, neutron) act like
tiny magnets. This is an intrinsic property known as spin.
– An electron has a N and a S pole !
• Spin is fundamental property of the universe (no one knows
why it exists) and is not the result of a particle spinning.
• Permanent magnets are a result of the spin of valence
electrons.
• The spin of the electron is the basis of new technology called
spintronics - digital information processing and storage using
electron spin instead of charge.
The Source of the Magnetic Field: Moving
Charges
The magnetic field of a charged particle q moving with
velocity v is given by the Biot-Savart law:
where r is the distance from the charge and θ is the angle
between v and r.
The Biot-Savart law can be written in terms of the cross
product as:
The Magnetic Field of a Moving Charge:
Direction of B from Right Hand Rule
! ! !
Vector Cross Product: A = C ! D
1)Curl fingers of right hand in the direction that moves the vector
C towards the vector D while passing through the smallest angle.
2)Thumb will point in the direction of the cross product (red arrow).
Evaluating Cross Product for Unit Vectors
! ! !
A = C ! D = (C1iˆ + C2 ĵ + C3 k̂) ! (D1iˆ + D2 ĵ + D3 k̂)
!
A = (C2 D3 " C3 D2 )iˆ + (C3 D1 " C1 D3 ) ĵ + (C1 D2 " C2 D1 )k̂
iˆ ! iˆ = ĵ ! ĵ = k̂ ! k̂ = 0
Tesla: Unit of Magnetic Field
1 Tesla= 1T= 1N/Am is the
fundamental unit of the
magnetic field strengt.
1 tesla is an enormous magnetic
field !
Some countries really
know how to honor their
engineers ! Nikola Tesla
was an electrical engineer:
1)AC Electric Motor
2)AC Power Transmission
3)Radio Communication
4)Remote Control
5)Logic circuits
6)Wireless energy transmission
7)Tesla coil
Biot-Savart Law for Currents
• Biot-Savart law for currents can
be used for any current geometry
although usually integral is very
difficult.
• It adds up the magnetic fields
produced by each length segment
ds, which has a current I
Biot-Savart Law: From a Moving Charge to a
Current (Derivation Review).
A current is a collection of moving charges.
Each moving charge produces it's own B-field
according to Biot-Savart Law.
!
!
q
v
µ j j " r̂
Bj = 0
4! r 2
!
!
!
q j v j " r̂
µ0
B = # Bj =
# r2
4! j
Treat each charge is as being contained in an infinitesimal
line segment ds:
!
ds dq !
!
!
q j v j $ dq =
ds = Ids
dt dt
! µ0 Ids! " r̂
B=
4! % r 2
! µ0 Ids! " r̂
dB =
4! r 2
The Magnetic Field of a Long Current Carrying Wire
We already know the direction of the B-field but what is the
magnitude?
!
dl ! r̂ = dysin(" / 2 + # )
x
x
= dy cos # = dy = dy
r
x 2 + y2
(
1/2
)
The Magnetic Field of a Current Loop
Many practical devices such as transformers, inductors,
and solenoid utilize the magnetic field produced by current loops.
The magnetic fields of the
connecting wires do not
contribute since their B-fields
cancel out (assuming they
lie side by side).
Current segments on opposite
sides of loop produce magnetic
fields with opposite x and y
components on axis.
On axis, the only magnetic field
is in the axis direction.
Deriving the Magnetic Field On Axis for Loop
!
!sk " r̂ = !sk
( Bk )z =
µ0 I !sk
µ0 I !sk
R
cos
$
=
4# r 2
4# ( z 2 + R 2 ) ( z 2 + R 2 )1/2
2#
Bz = % ( Bk ) &
k
z
2#
' dB =
0
µ
IR
Bz = 0
4# ( z 2 + R 2 )3/2
'
R d(
0
µ0
IR
4# ( z 2 + R 2 )3/2
A coil of N current
loops:
2#
' R d(
0
µ0
IR 2
Bz =
2 ( z 2 + R 2 )3/2
We can 'amplify' this magnetic field by stacking together N current loops
to make a coil. Assuming the length of the coil is negligible (wires stacked
essentially on top of each other), we have
µ0
NIR 2
Bz =
2 ( z 2 + R 2 )3/2
Ampère s law
Whenever total current I passes
through an area bounded by a
closed curve, the line integral
of the magnetic field around the
curve is given by Ampère s law:
! !
B
!
d
s
=
µ
I
"
0
Closed line integral
around the current
Ampere s Law for a Wire With Current I
! !
"! Bidl = µ0 I enc
! ! !
"! Bidl = B "! dl =B2" r
µ0 I enc
B=
2" r
Very easy calculation in comparison to
Biot-Savart law
For Ampere s Law: What Sign to Use for
Current???
Use right hand rule (again!) to determine sign of current.
Curl right fingers around
integration path. If thumb points
in direction of current, I is positive
in Ampere s law. If thumb points
opposite to direction of current,
I is negative in Ampere s law.
I enc = I 2 + I 4 ! I 3
Magnetic Field Inside Wire
Current Density: J = I / ! R 2
Solenoid
A solenoid is a long coil of wire with a current running through it.
Inside, away from the edges, the magnetic field is uniform and
along the axis.
Has many uses in technology:
1)Electromechanical switches (relays)
2)Automobile ignition systems
3)Hydraulic/pneumatic valves for controlling fluid/gas flow
4)Magnetic Resonance Imaging
5)Inductors (Chapters 34+36)
Real (Finite Length) Solenoids Have External
Magnetic Fields Like a Bar Magnet
An Electromechanical Switch Relay (Example
of Solenoid)
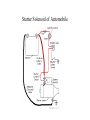
Starter Solenoid of Automobile
The Interior Magnetic Field of a Solenoid
! !
Use Ampere's Law: "
! Bidl = µ0 I enc
! !
! !
! !
! !
! !
"! Bidl = ! Bidl + ! Bidl + ! Bidl + ! Bidl
1
1
1
3
2
! !
! Bidl =
2
4
2
! !
! Bidl = 0
3
4
!
!
! !
! Bidl = 0 B " dl
3
! !
! Bidl = B ! dl = Bl
4
4
I enc = NI
&
N
( I = µ nI
B= µ
0 l ('
0
#
%
%
$
n = N/l is the number of turns per unit length.
Magnetic Dipoles
The external magnetic field produced by a current loop
or finite solenoid looks just like the magnetic field of
bar magnet.
Current loops form magnetic dipoles.
Magnetic Dipoles: B-Field
Current loops are magnetic dipoles!
Bloop
µ0
IR 2
µ0 2AI
=
!
2 ( z 2 + R 2 )3/2
4" z 3
z!R
Define the magnetic dipole moment:
"
µ = AIn̂
Use right hand rule
for normal vector !
When the size of the current loop is much smaller than the distance
at which the B field is measured,
" µ0 3( µ" ir̂)r̂ # µ"
B=
4"
r3
The magnetic field has the exact same form as the electric field of an
electric dipole !
The Magnetic Force on a Moving Charge
The magnetic force on a charge q
as it moves through a magnetic
field B with velocity v is
!
! !
F = qv ! B
If there is a magnetic and electric field,
the total force on the charge is:
!
! ! !
Fon q = q E + v ! B
(
)
This is equation is known as the Lorentz force
Behavior of the Magnetic Force
1)The magnetic field exerts no force on stationary charges !!
Moving charges create magnetic fields and only moving
charges feel a force from magnetic fields !!!
2)Motion parallel or anti-parallel to the magnetic field produces
no force !
B field is pointing
into the page
Magnetic Fields Do No Work
Recall the definition of the work done by a force on a particle
in going from position i to f:
sf !
!
W (i ! f ) = " Fids
si
Substitute in the magnetic force:
! !
! $ ds! '
sf !
sf !
WB = " v # B ids = " v # B i& dt )
si
si
% dt (
! !
sf !
WB = " v # B iv dt
si
!
!
!
v#B * v
! ! !
v # B i v = 0 ! WB = 0
(
(
)
(
)
(
)
)
The magnetic field does no work on the particle !
W=+K= change in kinetic energy
The magnetic field can not accelerate a particle !
Cathode Ray Tube (Older TVs and Computer
Monitors)
Magnetic Field: Uniform Circular Motion
(Cyclotron Motion)
• Force is always
perpendicular to velocity.
• Such a force is constantly
deflecting the particle
sideways.
• This causes particle to
move in a circle with a
constant velocity.
• Motion perpendicular to
B-field is unaffected.
Motion in a Plane Perpendicular to Magnetic
Field
F = qvB
magnetic force = centripetal force towards center
mv 2
qvB =
r
v (speed) is unchanged by B. Only r, radius of
orbit is variable:
mv
rcyc =
qB
Frequency of orbit:
v = !r
qB
! cyc = 2" f =
m
(! cyc is orbital frequency in radians per second)
The Hall Effect
The Hall effect was the first experiment to prove metals have
negative charge carriers.
It is used for:
1)Determining the sign and type of charge carriers in
conducting materials (particularly in new types of exotic materials).
2)As a sensor for measuring magnetic fields
3)Hall sensors used for motor/engine tachometers and
internal combustion engine timing.
Hall Effect: Magnetic Field Induces a Transverse
Voltage
Configuration: Current in
conducting bar with B field
perpendicular to bar. Lorentz
force causes moving charges to
be deflected towards sides where
they accumulate.
Positive Charge Carriers:
Negative Charge Carriers:
Hall Voltage Determines Sign of Charge Carriers
and Magnetic Field Strength
Charges are deflected to the side. The charge separation leads
to an electric field and, hence, potential difference between the sides.
Steady state: Electric Force Between Sides=Magnetic Force
FB = FE
FE = qE = q!VH / w
FB = qvd B
!VH = vd wB
However it is the current and not the drift velocity
that one measures in the lab:
vd = I / ( Anq )
!VH =
IB " w %
$ '
nq # A &
w = width of bar
A= cross sectional area
Magnetic Forces on Current-Carrying Wires
Consider a segment of wire of length l carrying current I in the direction of
the vector l. The wire exists in a constant magnetic field B. The magnetic
force on the wire is
!
! !
F = !Qv " B
The charge passing through a length l
of the wire is:
!Q = I !t
!x
l
v=
=
!t !t
! !
!
F = Il " B
!
l points in direction of current
where α is the angle between the direction of the current and the magnetic field.
l
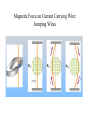
Magnetic Force on Current Carrying Wire:
Jumping Wires
Magnetic Force Between Two Parallel Wires
µ0 lI1 I 2
F2 || wires =
2! d
d = separation
l = length of wires
Currents in same direction : Attractive force
Currents in opposite directions: Repulsive force
Torques on Current Loops (Magnetic Dipoles)
The Lorentz force on the top and bottom
segments are opposite and rotate the current
loop. Therefore there is a torque on the current loop:
! ! !
! =µ"B
!
µ = IAn̂ = Il 2 n̂
Potential energy of a magnetic dipole in B field:
! !
U B = # µi B
This equations are valid for current loop dipoles
and permanent magnets (lik a compass needle)!
Electric Motor