Download Assignment 7 Solutions

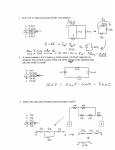
Assignment 7 Solutions
PY 106
1. A single-turn rectangular wire loop measures 6.00 cm wide by 10.0 cm long.
The loop carries a current of 5.00 A. The loop is in a uniform magnetic field
with B = 5.00 × 10−3 T. Taking torques about an axis, parallel to either side
of the rectangular loop, that maximizes the torque, what is the magnitude
of the torque exerted by the field on the loop if the direction of the magnetic
field is...
(a) parallel to the short sides of the loop?
We can figure out the forces experienced by each side using the right hand rule,
to get a good visualization of what’s causing the torque, and what direction it
would be in. However, we can also use the rule:
τ = IAB sin θ
where θ is the angle between the magnetic field and the area vector of the loop.
~ and A
~ are perpendicular, so:
In this case, B
τ = IAB = 5.00 A · (0.06 m × 0.1 m) · 5.00 × 10−3 T = 0.00015 Nm
(b) parallel to the long sides of the loop?
~ and A
~ are still perpendicular, so τ = 0.00015 Nm
We get the same answer here as B
(c) perpendicular to the plane of the loop?
~ and A
~ are parallel (because A
~ sticks out perpendicular to the
In this case, B
loop), so τ = 0 Nm
2. The picture below shows four different cases of a conducting square loop
(in orange), traveling at speed v and passing through a rectangular region.
In the left half of the rectangular region, the magnetic field is uniform and
directed into the screen; in the right half, the magnetic field is uniform
and directed out of the screen. The field has the same magnitude in each
half of the rectangular region, and there is no magnetic field outside the
rectangular region.
(a) Rank the four cases based on the magnitude of the total magnetic
flux passing through the loop, from largest to smallest, at the instant
shown in the picture. Use only > or = signs in your answer, such as
B > A = D > C.
Magnetic flux is:
1
Φ = BA cos θ
where θ is the angle between the magnetic field and the area vector. Since all these
loops are the same area, and their area vectors are all parallel to the magnetic
fields in the regions, all we have to look at to rank their fluxes is the magnitude
of the magnetic field enclosed within each loop. To do this, we can just consider
the amount of area each loop has in the regions:
• Loop A is half in the right region, and half into the left region. Since the
magnetic fields are of equal magnitude and in the opposite direction in the
regions, the total magnetic field within A is zero.
• Loop B is entirely within the left region, so it’s experiencing a magnetic field
into the page.
• Loop C, exactly like loop A has a zero magnetic field, as it is half in one
region and half in the other.
• Loop D is partially within the right region, so it’s experiencing a magnetic
field out of the page, but weaker than B.
Thus, the ranking is B > D > A = C
(b) Rank the four cases based on the magnitude of their induced current,
from largest to smallest, at the instant shown in the picture. Use only
> or = signs in your answer, such as B > A = D > C.
In order to figure this out, you must imagine each square moving just the slightest
bit into its current position, and look at the change in magnetic field that the
square experiences (again as the square’s area and angle remain constant).
• Loop A has just shifted slightly to the right, which means that it has lost a
bit of magnetic field going into the page and has gained some magnetic field
going out of the page. To fight this, A will induce a magnetic field going into
the page, i.e. a clockwise current.
• Loop B has just moved slightly to the right, which means that it stayed within
the into-the-page region, so there has been no change in magnetic field, and
thus no induced current
• Loop C has just moved slightly down, which means that the entire time, half
of it is in the left region and the other half is in the right region, i.e. no
magnetic field change, and no induced current.
• Loop D has just moved slightly to the right, so it has lost an amount of
out-of-the-page magnetic field. To fight this it induces a field going out of
the page, thus a counter-clockwise current. This induced current is less than
that of A, as the change in magnetic field that A experiences is greater.
Thus, the ranking is A > D > B = C
(c) Choose the four correct statements, from the list below, regarding the
direction of the induced current in each case, at the instant shown in
the picture above.
•
•
•
•
There is no induced current in case A.
The induced current in case A is directed clockwise.
The induced current in case A is directed counter-clockwise.
There is no induced current in case B.
2
•
•
•
•
•
•
•
•
The induced current in case B is directed clockwise.
The induced current in case B is directed counter-clockwise.
There is no induced current in case C.
The induced current in case C is directed clockwise.
The induced current in case C is directed counter-clockwise.
There is no induced current in case D.
The induced current in case D is directed clockwise.
The induced current in case D is directed counter-clockwise.
3. In this simulation the current in a long straight wire produces a magnetic
field. Depending on what is happening to the current in that wire, there
may or may not be a current induced in the conducting loop shown to the
right of the wire. An ammeter measures the current in the loop. Try moving
the slider, which controls the current in the wire, to see what happens to
the current in the loop.
(a) The current in the loop is sometimes positive and sometimes negative. Under
what condition is the current in the loop a positive value?
• When the magnetic field produced by the long straight wire is directed out
of the screen when it passes through the loop. No
• When the magnetic field produced by the long straight wire is directed into
the screen when it passes through the loop. No
• When the current in the loop is clockwise. No
• When the current in the loop is counter-clockwise. Yes
(b) Which of the following statements about this situation are true? Select all that
apply.
• To produce a positive current in the loop, the current in the wire must be
positive.
• To produce a positive current in the loop, the current in the wire must be
negative.
• To produce a positive current in the loop, the current in the wire must be
getting more positive (or less negative). Yes
• To produce a positive current in the loop, the current in the wire must be
getting more negative (or less positive).
• To produce a current in the loop, the current in the wire must be changing,
but it makes no difference how fast the current in the wire changes.
• To produce a current in the loop, the current in the wire must be changing.
The faster the current in the wire changes, the larger the magnitude of the
current in the loop. Yes
Your answer is incorrect.
4. The picture below shows four conducting loops, labeled A through D, that
are moving in the indicated direction near a long straight wire that is carrying a constant current to the right. The picture on the right is a similar
situation, except in that picture loops E and F are at rest and the current is
decreasing in magnitude. In what direction (clockwise or counter-clockwise
or none) is the induced current in each loop?
3
The areas of all these loops are the same, so we don’t have to worry about the change
in their areas. All of these loops are experiencing a magnetic field from the currentcarrying wire, which has a magnetic field going out of the page on the top half and
going into the page on the bottom half of the wire. This means each loop’s area vector
and the magnetic field are parallel. All we have to worry about when looking at the
change in magnetic flux, is the change in magnetic field, so let’s look at each case:
• Loop A: Since the loop is approaching the current-carrying wire, the B field Loop
A experiences increases with time. This magnetic field is directed out of the page
(as you can see with the right-hand-rule), so in order to fight this increase, Loop
A will induce a magnetic field going into the page, which corresponds with a
CW current.
• Loop B: The loop is going away from the current-carrying wire, so the magnetic
field (out of the page) that it experiences decreases. To fight this change, loop
B will induce a magnetic field going out of the page, which corresponds to a
CCW induced current.
• Loop C: This loop is moving parallel to the current-carrying wire, so the magnetic
field inside it isn’t changing at all. So there is no induced current.
• Loop D: The loop is approaching the current-carrying wire, so the into-the-page
magnetic field is increasing. To fight this, the loop will induce a magnetic field
going out of the page, which corresponds with a CCW induced current.
• Loop E: The current in the current-carrying wire is decreasing, so the out-of-thepage magnetic field experienced by loop E will decrease. To fight this, E will induce a magnetic field going out of the page, which means a CCW induced current.
• Loop F: The current in the current-carrying wire is decreasing, so the into-thepage magnetic field experienced by loop F will decrease. To fight this, F will induce
a magnetic field going into the page, which means a CW induced current.
5. A flat coil of wire, consisting of 20 circular loops with a total resistance of
20.0 ohms, is placed so that it is at rest, flat on a table. The graphs below
show the magnetic flux through each loop of the coil as a function of time,
for three different cases. The units of flux are webers, which are equivalent
to tesla meters2 . The flux through each loop changes because the magnetic
field changes . Assume that the field is uniform and the direction of the
field is perpendicular to the plane of the coil - positive flux means the field
is passing in one direction through the coil, and negative flux means that
the field is passing through the coil in the opposite direction.
(a) Rank the cases based on the magnitude of the flux passing through
each loop of the coil at a time of t = 23 s, from largest to smallest. Only
use > and/or = signs in your answer, such as A > B > C.
4
Since the graphs show flux vs time, we can just read off the values at t = 23 s.
Since we’re just looking at a magnitude, and not worrying about signs, this gives
us the ranking C > A > B .
(b) Rank the cases based on the magnitude of the induced current in the
coil at a time of t = 23 s, from largest to smallest. Only use > and/or
= signs in your answer, such as A > B > C.
Remember that induced current is given by:
I=
ǫ
∆Φ 1
= −N
·
R
∆t R
so to compare the induced currents, we have to look at the slope of each graph
(which gives us ∆Φ
), as all the other quantities (N and R) are constant between
∆t
the identical loops. Graphs A and B have the same magnitude slope at t = 23 s
(even though B has a negative slope), and C is completely flat there, so it has a
zero slope. The ranking, then is A = B > C .
(c) In Case A, calculate the magnitude of the induced current in the loop at t = 6 s.
To calculate the magnitude of the induced current, we just have to plug in values
to the equation in part (b). Here, the slope at t = 6 s is:
0.4 W
∆Φ
=
= 0.08 W/s
∆t
5s
So the magnitude of our induced current is:
I =N
∆Φ 1
20 · 0.08 W/s
· =
= 0.08 A
∆t R
20Ω
(d) In Case C, calculate the magnitude of the induced current in the loop
at t = 17.5 s.
We do the same thing here. Our slope is:
∆Φ
−0.4 W
=
= −0.08 W/s
∆t
5s
which is coincidentally the same magnitude slope as in part (c), so we should get
the same induced current:
I =N
∆Φ 1
20 · 0.08 W/s
· =
= 0.08 A
∆t R
20Ω
6. (a) A Boeing 747 has a wingspan of 64 m. If the jet is flying north at a speed of 730
km/h in a region where the vertical component of the Earth’s magnetic field is
3.90×10−5 T, directed down, what is the magnitude of the motional emf measured
from wingtip to wingtip?
To understand why there’s an emf across the airplane, imagine tiny positive and
negative charges within the plane. Each of these charges are travelling at a velocity
v to the north, and are experiencing a downward (i.e. into the page) magnetic
field. This means the positive charges experience a force to the west, and the
negative charges experience a force to the east (using the right-hand-rule). So the
higher the velocity of the plane, or the stronger the magnetic field, or the shorter
5
the distance the charges would have to travel, the higher the emf. We can write
an equation:
ǫ = vdB
where d is the length of the wingspan. Plugging in our value (and converting v
into m/s gives us:
ǫ = vdB = 202.7 m/s · 64 m · 3.90 × 10−5 T = 0.506 V
(b) Which wingtip is at a higher potential?
Since the positive charges pile up on the west wingtip, and the negative charges
pile up on the east, the potential is higher at the west wingtip . To understand
this, imagine putting a positive test charge on each side. The test charge is
“happier” to be next to all the negative charges, which means it’s at a lower
potential there.
7. A square loop consists of a single turn with a resistance of 5.00 Ω. The loop
has an area of 200 cm2 , and has a uniform magnetic field passing through
it that is directed out of the page. The loop contains a 12-volt battery,
connected as shown in the figure above.
(a) At the instant shown in the figure, there is no net current in the loop.
At what rate is the magnetic field changing? Use a positive sign if the
field is increasing and magnitude, and a negative sign if the field is
decreasing in magnitude.
Since there’s no net current, we know there’s no net potential. So we know that
the change in magnetic flux must be inducing an emf that is equal in magnitude
to the battery’s emf, but opposite in direction. Note that a counter-clockwise
induced current would satisfy this, and that would lead to an induced magnetic
field out of the page. In order for the loop to induce a magnetic field out of the
page, the magnetic field in the image must be decreasing (so we should remember
to use a minus sign in the answer).
So:
12 V = ǫ = −N
∆Φ
∆t
~ and A
~ are parallel throughout
But here, since the area A isn’t changing, and B
this process,
∆Φ = ∆(BA cos θ) = A cos θ∆B = A∆B
Plugging this in (along with N = 1) gives us:
12 V = A
∆B
∆t
We re-arrange this and remember to convert our area to m2 to get:
∆B
12 V
12 V
=−
=−
= -600 T/s
∆t
A
0.02 m2
6
(b) If the polarity of the battery was reversed, and the magnetic field
was still changing at the rate you calculated above, what would the
magnitude of the net current through the loop be?
If the polarity of the battery is reversed, the emf from the battery will now add
to the emf from the magnetic field, so the total emf would now be 12 V + 12 V =
24 V. Since we have a resistance, we can calculate the current using Ohm’s Law:
I=
24 V
V
=
= 4.8 A
R
5.0Ω
7