* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download week5
Drug discovery wikipedia , lookup
Discovery and development of cephalosporins wikipedia , lookup
5-HT3 antagonist wikipedia , lookup
Metalloprotease inhibitor wikipedia , lookup
Discovery and development of angiotensin receptor blockers wikipedia , lookup
Discovery and development of non-nucleoside reverse-transcriptase inhibitors wikipedia , lookup
Discovery and development of neuraminidase inhibitors wikipedia , lookup
Discovery and development of tubulin inhibitors wikipedia , lookup
Discovery and development of direct Xa inhibitors wikipedia , lookup
Nicotinic agonist wikipedia , lookup
Discovery and development of integrase inhibitors wikipedia , lookup
Neuropharmacology wikipedia , lookup
Discovery and development of ACE inhibitors wikipedia , lookup
NK1 receptor antagonist wikipedia , lookup
Discovery and development of antiandrogens wikipedia , lookup
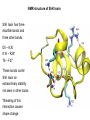
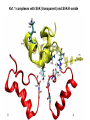
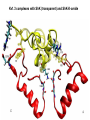
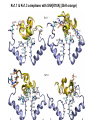
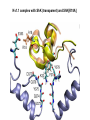
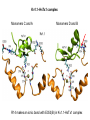
Week 5 MD simulations of protein-ligand interactions • Lecture 9: Fundamental problems in description of ligand binding to proteins: i) determination of the complex structure, ii) calculation of free energy of binding. Using docking with MD simulations to find structures for protein-ligand complexes. Validating complex structures using mutation data and binding free energies. Example from binding of ShK toxin from sea anemone to Kv1 channels. • Lecture 10: Rational design of a selective ShK analog for treatment of autoimmune diseases using FEP/TI methods. Computational study of a better candidate from the spider toxin HsTx1. Problems and prospects for Nav channel toxins. Why study proteinligand interactions? • Quantitative description of protein–ligand interactions is a fundamental problem in molecular biology • Pharmacological motivation: drug discovery is getting harder searching compound libraries using experimental methods. Using computational methods and peptide ligands from Nature (e.g. toxins) offer alternative methods and means for drug discovery • Computational methods would be very helpful in drug design but their accuracy needs to be confirmed for larger, charged peptide ligands • Proof of concept study: Binding of charybdotoxin to KcsA* (Shaker) Realistic case study: Binding of ShK toxin and analogs to Kv1.1, Kv1.2, and Kv1.3 channels Two essential criteria for development of drug leads 1. Should bind to a given target protein with high affinity 2. Be selective for the target protein The first issue is addressed with many experimental (e.g. High Throughput Screening) and computational methods (e.g. docking), and there is a huge data base about high affinity ligands. The second issue is harder to address with traditional methods and would especially benefit from a rational drug design approach. Example: Kv1.3 is one of the main targets for autoimmune diseases • ShK toxin binds to Kv1.3 with pM affinity • But it also binds to Kv1.1 in the nervous system with pM affinity • Need to improve selectivity of ShK for Kv1.3 over Kv1.1 Challenges in computational design of drugs from peptides 1. Apart from a few cases, the complex structure is not known. Assuming that structures (or homology models) of protein and ligand are known, the complex structure can be determined via docking followed by refinement with MD simulations. 2. Affinity and selectivity of a set of ligands for target proteins need to be determined with chemical accuracy (1 kcal/mol). Binding free energies can be calculated accurately from umbrella sampling MD simulations. For selectivity, one could use the free energy perturbation (FEP) method (computationally cheaper). The FEP method is especially useful if one is trying to improve selectivity via minor modifications/mutations of a ligand. Computational program for rational drug design from peptides 1. Complex structure determination: Find the initial configuration for the bound complex using a docking algorithm (e.g., HADDOCK). Refine the initial complex(es) via MD simulations. 2. Validation: a) Determine the key contact residues involved in the binding and compare with available mutagenesis data to validate the complex model. b) Calculate the potential of mean force for the ligand to determine the binding constant and free energy, and compare with experiments. 3. Design: Consider mutations of the key residues on the ligand and calculate their binding free energies (relative to the wild type) using the free energy methods. Those with higher affinity/selectivity are candidates for new drugs. Proof of concept study: Binding of charybdotoxin (ChTx) to KcsA* (Shaker Kv mimic) • Complex structure is determined from NMR, so it provides a unique test case for MD simulations of peptide binding. • Using HADDOCK for docking followed by refinement via MD simulations reproduces the experimental complex structure. • Binding free energy of ChTx calculated from the potential of mean force (PMF): -7.6 kcal/mol • Experimental value: -8.3 kcal/mol • Agreement within 1 kcal/mol Structure of the KcsA*- ChTx complex Important pairs: K27 - Y78 (ABCD) R34 - D80 (D) R25 - D64, D80 (C) K11 - D64 (B) K27 is the pore inserting lysine – a common thread in scorpion and other potassium channel toxins. K11 R34 Realistic case study: ShK toxin binding to Kv1 channels • Motivation: – Kv1.3 is the main target for autoimmune diseases – ShK binds to Kv1.3 with pM affinity (but also to Kv1.1) – – Need to improve selectivity of ShK for Kv1.3 over Kv1.1 Some 400 ShK analogs have been developed for this purpose 1. Find the complex structures of ShK with Kv1.1, Kv1.2 and Kv1.3, and validate them using mutagenesis data. Determine the PMFs and the binding free energy and compare with experiment for further validation. Use the binding mode to predict mutations that will improve the Kv1.3/Kv1.1 selectivity. 2. Repeat the above study for ShK-K-amide (an analog with improved Kv1.3/Kv1.1 selectivity) to rationalize the experimental results. NMR structure of ShK toxin ShK toxin has three disulfide bonds and three other bonds: D5 – K30 K18 – R24* T6 – F27 These bonds confer ShK toxin an extraordinary stability not seen in other toxins. *Breaking of this interaction causes shape change. Homology model of Kv1.3 Can be obtained from the crystal structure of Kv1.2 (over 90% homology and 1-1 correspondence between residues). Note: care must be exercised for the V H404 mutation because H404-D402 side chains cross link which can be broken during equilibration (several publications have the wrong Kv1.3 structure because of this). Kv1.1-ShK complex Monomers A and C Monomers B and D Kv1.3-ShK complex Monomers A and C Monomers B and D Pair distances in the Kv1.3-ShK complex (in A) Kv1.3 ShK Dock. MD av. Exp. D376–O1(C) R1–N1 5.0 4.5 S378–O(B) H19–N 3.2 3.0 ** Y400–O(ABD) K22–N1 2.9 2.7 ** G401–O(B) S20–OH 2.9 2.7 ** G401–O(A) Y23–OH 3.5 3.5 ** D402–O(A) R11–N2 3.2 3.5 * H404-C(C) F27-Ce1 9.7 3.6 * V406–C1(B) M21–Ce 9.4 4.7 * D376–O1(C) R29–N1 12.2 10.2 * HADDOCK is not very good for hydrophobic int’s ** strong, * intermediate ints. (from alanine scanning Raucher, 1998) R24 (**) is not in the complex (allosteric effect due to shape change.) Average pair distance as a function of umbrella window positions ** denotes strong coupling and * intermediate coupling * * ** ** * ** ** RMSD of ShK as a function of umbrella window The RMSD of ShK relative to the NMR structure remains flat throughout Overlap of the neighbouring windows Gaussian dist: % overlap 1 erf (d / 8 ), d : distance , k BT / k For k=30 kcal/mol/A2, the overlap is about 10% in bulk, which is an overlap optimal value for umbrella simulations (only one extra window needed) Convergence of the PMF for the Kv1.3-ShK complex PMF of ShK for Kv1.1, Kv1.2, and Kv1.3 Average pair distances in Kv1.2–ShK from umbrella sampling Comparison of the binding free energies of ShK and its analogs to Kv1.x channels Complex Gb(PMF) Gb(exp) (kcal/mol) Kv1.1–ShK -14.3 ± 0.6 -14.7 ± 0.1 Kv1.2–ShK -10.1 ± 0.6 -11.0 ± 0.1 Kv1.3–ShK -14.2 ± 0.7 -14.9 ± 0.1 Kv1.1-ShK-K-amide -11.8 ± 1.0 -12.3 ± 0.1 Kv1.3-ShK-K-amide -14.0 ± 0.4 -14.4 ± 0.1 Kv1.1-ShK[K18A] -11.7 ± 0.7 -11.3 ± 0.1 Kv1.3-ShK[K18A] -13.9 ± 0.6 -14.2 ± 0.1 Good agreement with experimental values for all channels, which provides an independent test for the accuracy of the complex models. Kv1.1 complexes with ShK (transparent) and ShK-K-amide Kv1.3 complexes with ShK (transparent) and ShK-K-amide Computational design of Kv1.3/Kv1.1 selective analogs The voltage-gated potassium channel Kv1.3 in lymphocytes is overexpressed during autoimmune attacks. Thus blocking it with a high- affinity ligand could provide a valuable therapeutic agent. 1.ShK toxin from sea anemone binds to Kv1.3 with picomolar affinity, and has therefore attracted a great deal of attention. But lack of selectivity over Kv1.1 prevented its use as a potential drug. Using computational methods, new selective analogs of ShK have been predicted. 2.The scorpion toxin HsTx1 has already some Kv1.3/Kv1.1 selectivity and could provide a better candidate for selective blocking of Kv1.3. However, due to patenting issues, it has not been considered in the past. An HsTx1 analog with improved selectivity has been predicted from computations and confirmed experimentally (now patented). Application 1: Design of autoimmune drugs from the ShK toxin • All the single and some double mutations in ShK have been patented by a pharmacology company (AMGEN), which indicated that none are useful for design of a Kv1.3/Kv1.1 selective analog. • As a result, these mutations have not been considered in addressing the selectivity problem. Instead people have been looking for analogs with non-natural AA and adducts. Over 400 analogs of ShK were developed at the Norton Lab (Melbourne) but only a few had some Kv1.3/Kv1.1 selectivity. • The Kv1–ShK complex structures indicate several mutations that should improve Kv1.3/Kv1.1 selectivity (e.g. K18A, R29A). The K18A mutation does not change the binding mode in either Kv1.1–ShK or Kv1.3–ShK complex (while R29A does). Thus first consider the K18A analog. • Test case: use both the FEP/TI and PMF calculations to predict the free energy change due to the K18A mutation. Kv1.1 & Kv1.3 complexes with ShK[K18A] (ShK orange) Kv1.1 complex with ShK (transparent) and ShK[K18A] Free energy perturbation calculations for ShK[K18A] • The K18A mutation does not change the binding mode in either Kv1.1– ShK or Kv1.3–ShK complex. Thus one can use FEP calculations to find the free energy change due to the mutation. • Straightforward FEP calculation of the K18A mutation does not work. • Split the Coulomb and Lennard-Jones parts and do a staged FEP calculation • In the binding site, K K0 A0 A, while in the bulk follow the opposite cycle, i.e., A A0 K0 K • Add the three contributions from K K0 , K0 A0 and A0 A steps to find the binding free energy difference, DDG(K A) • Simultaneous calculation of binding site/bulk avoids issues with charge neutrality and simulation artefacts arising from using different systems. Thermodynamic cycle for the FEP/TI calculations DDGb DGb (ShK[K18A] ) DGb (ShK) PMF DDG (K K 0 ) DDG (K 0 A 0 ) DDG (A 0 A) FEP/TI Convergence of the FEP calculations for K K0 and K0 A0 Kv1.1 Kv1.3 Convergence of the TI calculations for K K0 Kv1.1 Kv1.3 The forward and backward TI calculations agree within 1 kcal/mol. Thus there are no hysteresis effects due to inadequate sampling. Effect of the K18A mutation on binding free energies Binding free energy differences for Kv1.1 and Kv1.3, and the selectivity free energy for Kv1.3/Kv1.1. (in units of kcal/mol) ∆∆Gb(Kv1.1) ∆∆Gb(Kv1.3) ∆∆Gsel FEP 2.1 0.5 1.6 TI 2.4 0.2 2.2 PMF 2.7 0.4 2.3 Exp. 3.1 0.8 2.3 DDGb DGb (ShK[K18A] ) DGb (ShK ) DDGsel DDGb (Kv1.1) DGb (Kv1.3) ShK[K18A] enhances Kv1.3/Kv1.1 selectivity by 2.3 kcal/mol Double and triple mutations in ShK • The K18A mutation provides some gain in Kv1.3/Kv1.1 selectivity but this is not sufficient for drug safety. Need to increase the selectivity margin to > 4 kcal/mol. • Further mutations/additions in ShK could help. Candidates: – R29A changes the binding mode so it does not work – Mutation of R29 to a bulky hydrophobic residue preserves the binding mode and is likely to help – F27 has a stronger interaction with Kv1.1, so its mutation to a smaller hydrophobic residue could also help. – A triple mutation that involves K18, R29 and F27 is likely to achieve the desired selectivity margin. Application 2: Design of drugs from the scorpion toxin HsTx1 HsTx1 toxin from scorpion has already over hundred-fold selectivity for Kv1.3 over Kv1.1, but it is ignored because natural products cannot be patented. We studied binding of HsTx1 to Kv channels to understand the basis of this selectivity, and predicted a mutation that will enhance Kv1.3/Kv1.1 selectivity. • Prediction of Kv1.x-HsTx1 complex structures • Validation from binding free energies • Design of a HsTx1 analog with enhanced Kv1.3/Kv1.1 selectivity NMR structure of HsTx1 toxin HsTx1 toxin has four disulfide bonds and hydrogen bonds between: A1 – C29 C3 – R27 These bonds confer HsTx1 toxin an even more stable structure than ShK toxin! Pore inserting lysine Comparison of Ca RMSDs in ShK and HsTx1 Kv1.1–HsTx1 complex Monomers C and A Monomers D and B R14 makes an ionic bond with E353(B) in Kv1.1-HsTx1 complex Kv1.3–HsTx1 complex Monomers C and A Monomers D and B R14 does not interact with any Kv1.3 residues in Kv1.3-HsTx1 complex RMSD of HsTx1 as a function of umbrella window RMSDs of HsTx1 relative to the NMR structure – no shape change. Convergence of the PMFs for the Kv1.x–HsTx1 complexes Convergence of the PMF is much slower in Kv1.1 compared to Kv1.3. This example highlights the danger of choosing an arbitrary time (e.g. 1 ns) for equilibration in PMF calculations. PMFs for the Kv1.x–HsTx1 complexes Comparison of the binding free energies for Kv1.x–HsTx1 complexes to experimental values Complex Gb(PMF) Gb(exp) (kcal/mol) Kv1.1–HsTx1 -10.1 ± 0.6 -11.1 ± 0.1 Kv1.2–HsTx1 -8.9 ± 0.6 > -9.6 ± 0.1 Kv1.3–HsTx1 -14.0 ± 0.7 -14.9 ± 0.2 Good agreement with experimental values for all channels, which provides a test for the accuracy of the complex models. Note that there are no alanine scanning data available for HsTx1 binding to Kv1.x channels. So we have to rely on binding free energies for validation. Design of a HsTx1 analog with enhanced Kv1.3/Kv1.1 selectivity The Kv1.3/Kv1.1 selectivity of HsTx1 is already ~ 4 kcal/mol. Free energy calculations show that the R14A mutation reduces the affinity of HsTx1[R14A] to Kv1.1 by a further 2.7 kcal/mol without affecting its affinity to Kv1.3 (confirmed in subsequent experiments). Thus HsTx1[R14A] provides an excellent candidate for development of a drug for treatment of autoimmune diseases. References (H. Rashid et al.): ShK : J. Phys. Chem. B 116: 4812 (2012) ShK[K18A] : PLoS One 8: e78 (2013) HsTx1 : J. Phys. Chem. B 118: 707 (2014) HsTx1[R14A] : Sci. Reps. 4: 4509 (2014) Problems and prospects for Nav channel toxins • Nav channels are even more important therapeutic targets than Kv • Bacterial Nav structures are not very useful for modelling of mammalian Nav channels but a reliable homology model for the pore domain is now available. • Pore domain of all Nav1.1 – Nav1.9 channels are very similar. There are differences in the turret region, which could play important roles in toxin binding. However no templates can be found for modelling the turret regions. • Another target is the voltage sensor. Disabling the voltage sensor of Nav1.7 selectively by binding toxin peptides could provide novel drugs for chronic pain. • Finally blocking the inner cavity from inside offers treatments for heart diseases. Summary • Reliable protein-ligand complex structures can be obtained using docking methods followed by refinement via MD simulations. (Complex models have been validated via mutagenesis data) . • Binding free energies and can be determined near chemical accuracy (i.e., 1 kcal/mol) from PMF. • Once a protein-ligand complex is characterized, one can study the effects of mutations on the ligand by performing FEP calculations, provided that the binding mode is preserved. These will be especially useful when seeking mutations that will increase affinity or improve selectivity of a given ligand targeting a specific protein.