Download Class26

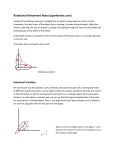
Class 26 - Rotation
Chapter 10 - Monday October 25th
•Review
Kinetic energy, moment of inertia, parallel axis theorem
•Newton's second law for rotation
•Work, power and rotational kinetic energy
•Sample problems
Reading: pages 241 thru 263 (chapter 10) in HRW
Read and understand the sample problems
Assigned problems from chapter 10 (due Sunday
October 31st at 11pm):
2, 10, 28, 30, 36, 44, 48, 54, 58, 64, 78, 124
Kinetic energy of rotation
K  12 I 2
I   mi ri 2

Therefore, for a continuous rigid object: I  r 2 dm 
2

r
 dV
Parallel axis theorem
Icom
h
rotation c.o.m.
axis
axis
•If moment of inertia is known about
an axis though the center of mass
(c.o.m.), then the moment of inertia
about any parallel axis is:
I  I com  Mh 2
•It is essential that these axes are
parallel; as you can see from table
10-2, the moments of inertia can be
different for different axes.
Some rotational inertia
Torque
•The ability to rotate an object about an
axis depends not only on the force you
apply, but also where and in what
direction you apply the force.
•In particular, the further away from
the axis that you push, the easier it is to
rotate the object.
•We define a quantity called torque, :
   r  F sin  
•The SI unit for torque is N.m, which is
the same as that for work (joule).
•However, torque and work are quite
different and should not be confused.
Torque
•There are two ways to compute torque:
   r  F sin    rFt
  r sin   F   r F
•The direction of the force vector is
called the line of action, and r is called
the moment arm.
•The first equation shows that the
torque is equivalently given by the
component of force tangential to the
line joining the axis and the point where
the force acts.
•In this case, r is the moment arm of Ft.
Torque
•Torque is actually a vector quantity
given by the following vector product:
  r F
•Thus, torques add like vectors, i.e. if
several torques act on an object, the net
torque net is given by the vector sum.
•In this chapter, you will not need
to worry about the vector
character of , since we shall only
consider rotational motion about
a fixed axis.
Newton's second law for rotation
•We can relate Ft to the tangential
acceleration using Newton's second law:
Ft  mat
•The torque  is then given by:
  Ft r  mat r
 m  r  r
  mr 
Substituting
r for at.
2
  I
For a rigid body which is free to rotate about a
fixed axis, Fr cannot affect the motion.
Work and rotational kinetic energy
K  K f  K i  12 I 2f  12 Ii2  W
(Work-kinetic energy theorem)
•By now, you should be noticing a pattern in the connections
between linear and angular equations: x  ; v  ; a  ;
m  I; F  , etc..
•Then, kinetic energy is calculated by substituting the linear
variables by their corresponding angular variables.
•We can do the same for work and power.
f
W    d
i
W    f   i 
dW
P
 
dt
(Work, rotation about a fixed axis)
(Work at constant torque)
(Power, rotation about a fixed axis)
Summarizing relations for translational and
rotational motion
•Note: work obtained by multiplying torque by an angle - a
dimensionless quantity. Thus, torque and work have the same
dimensions, but you see that they are quite different.