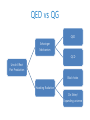
* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Can the vacuum energy be dark matter?
Symmetry in quantum mechanics wikipedia , lookup
Matter wave wikipedia , lookup
X-ray fluorescence wikipedia , lookup
Topological quantum field theory wikipedia , lookup
Path integral formulation wikipedia , lookup
Particle in a box wikipedia , lookup
History of quantum field theory wikipedia , lookup
Quantum chromodynamics wikipedia , lookup
Relativistic quantum mechanics wikipedia , lookup
Wave–particle duality wikipedia , lookup
Zero-point energy wikipedia , lookup
Casimir effect wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Renormalization wikipedia , lookup
AdS/CFT correspondence wikipedia , lookup
Canonical quantization wikipedia , lookup
Can the Vacuum Energy be Dark Energy? Sang Pyo Kim Kunsan Nat’l Univ. Seminar at Yonsei Univ. Oct. 29,2010 (Talk at COSMO/CosPA, Sept. 30, 2010, U. Tokyo) Outline • Motivation • Classical and Quantum Aspects of de Sitter Space • Polyakov’s Cosmic Laser • Effective Action for Gravity • Conclusion FLRW Universe • The large scale structure of the universe is homogeneous and isotropic, described by the metric 2 dr 2 2 2 2 2 2 2 ds dt a (t ) r (d sin d ) 2 1 Kr • The theory for gravity is Einstein gravity G g 8GT a(tobs ) • Friedmann equations in terms of the redshift 1 z a(tem ) 2 a 2 2 4 3 2 H ( z ) H 0 [ R 0 (1 z ) M 0 (1 z ) K 0 (1 z ) 0 ] a a 1 2 4 H 0 [ R 0 (1 z ) M 0 (1 z ) 3 0 ] a 2 Hubble Parameter & Dark Energy • Radiation H 2 ( z ) H 02 R 0 (1 z ) 4 • Matter H 2 ( z ) H 02 M 0 (1 z )3 • Curvature H 2 ( z ) H 02 K 0 (1 z ) 2 • Cosmological constant H 2 ( z ) H 02 0 WMAP-5 year data Dark Energy Models [Copeland, Sami, Tsujikawa, hep-th/0603057] • Cosmological constant w/wo quantum gravity. • Modified gravity: how to reconcile the QG scale with ? – f(R) gravities – DGP model • Scalar field models: where do these fields come from?(origin) – – – – – – Quintessence K-essence Tachyon field Phantom (ghost) field Dilatonic dark energy Chaplygin gas Vacuum Energy and • Vacuum energy of fundamental fields due to quantum fluctuations (uncertainty principle): – massive scalar: 4 1 cut d 3k 2 2 cut vac m k 2 0 (2 )3 16 2 – Planck scale cut-off: – present value: 10 47 (GeV ) 4 8G 71 4 10 ( GeV ) vac – order of 120 difference for the Planck scale cut-off and order 40 for the QCD scale cut-off – Casimir force from vacuum fluctuations is physical. Vacuum Energy in an Expanding Universe • What is the effect of the expansion of the universe on the vacuum energy? • Unless it decays into light particles, it will fluctuate around the minimum forever! • The vacuum energy from the effective action in an expanding universe? Vacuum Energy and • The uncertainty principle prevents the vacuum energy from vanishing, unless some mechanism cancels it. • Cosmological constant problem – how to resolve the huge gap? – renormalization, for instance, spinor QED 2 m 2 s / qE (qE ) e sp Leff ds [cot( s) 1 / s s / 3] 2 0 2 8 s vacuum energy charge – SUSY, for instance, scalar and spinor QED with the same spin multiplicity (nature breaks SUSY if any) L L sp eff sc eff (qE ) 8 2 2 0 ds e m 2 s / qE s 2 cot( s) 1 / sin( s) Why de Sitter Space in Cosmology? • The Universe dominated by dark energy is an asymptotically de Sitter space. • CDM model is consistent with CMB data (WMAP+ACT+) • The Universe with is a pure de Sitter space with the Hubble constant H= (/3). . • The “cosmic laser” mechanism depletes curvature and may help solving the cosmological constant problem [Polyakov, NPB834(2010); NPB797(2008)]. • de Sitter/anti de Sitter spaces are spacetimes where quantum effects, such as IR effects and vacuum structure, may be better understood. Classical de Sitter Spaces • Global coordinates of (D=d+1) dimensional de Sitter ds 2 dt 2 cosh 2 ( Ht )d 2d / H 2 embedded into (D+1) dimensional Minkowski spacetime ab X a X b 1 / H 2 , ds 2 ab dX a dX b ab X a X b 1 / H 2 , ds 2 ab dX a dX b has the O(D,1) symmetry. • The Euclidean space (Wick-rotated) has the O(D+1) symmetry (maximally spacetime symmetry). BD-Vacuum in de Sitter Spaces • The quantum theory in dS spaces is still an issue of controversy and debates since Chernikov and Tagirov (1968): -The Bunch-Davies vacuum (Euclidean vacuum, in-/informalism) leads to the real effective action, implying no particle production in any dimensions, but exhibits a thermal state: Euclidean Green function (KMS property of thermal Green function) has the periodicity 1 / TdS 2 / H -The BD vacuum respects the dS symmetry in the same way the Minkowski vacuum respects the Lorentz symmetry. BD-Vacuum in de Sitter Spaces • BUT, in cosmology, an expanding (FRW) spacetime 2 dr 2 2 2 2 2 ds dt a (t ) r d 2 2 1 kr does not have a Euclidean counterpart for general a(t). The dS spaces are an exception: 1 Ht 1 a(t ) e , a(t ) cosh( Ht ) H H Further, particle production in the expanding FRW spacetime [L. Parker, PR 183 (1969)] is a concept well accepted by GR community. Polyakov’s Cosmic Laser • Cosmic Lasers: particle production a la Schwinger mechanism -The in-/out-formalism (t = ) predicts particle production only in even dimensions [Mottola, PRD 31 (1985); Bousso, PRD 65 (2002)]. -The in-/out-formalism is consistent with the composition principle [Polyakov,NPB(2008),(2008)]: the Feynman prescription for a free particle propagating on a stable manifold G ( x, x' ) P ( x , x ') e imL( P ) dyG( x, y)G( y, x' ) P ( x , x ') L ( P )e imL( P ) G ( x, x ' ) m Radiation in de Sitter Spaces • QFT in dS space: the time-component equation for a massive scalar in dS cosh( Ht ) d / 2 (t , ) a (t ) uk ()k (t ); a H k 2uk () k 2uk (); (t ) Q (t ) (t ) 0 k k k 2 l (l d 1) k k d (d 2) a d a 2 Qk (t ) m 2 a 4 a 2 a 2 2 Radiation in de Sitter Spaces • The Hamilton-Jacobi equation in complex time k (t ) e iS k (t ) ; S k (t ) 2 ( H ) Qk ( z )dz; Qk (t ) 2 cosh 2 ( Ht ) d (d 2) dH 2 m ; l (l d 1) 4 2 2 2 2 k k (t ) e 2 2 Im S k ( t ) Stokes Phenomenon • Four turning points [figure adopted from Dumlu & Dunne, PRL 104 (2010)] e Ht( a ) H (H ) 2 i i 1 2 e Ht( b ) H (H ) 2 i i 1 2 • Hamilton-Jacobi action S k (t( a ) , t(b ) ) i H Radiation in de Sitter Spaces • One may use the phase-integral approximation and find the mean number of produced particles [SPK, JHEP09(2010)054]. Nk e 2 Im S ( I ) e 2 Im S ( II ) 2 cos(Re S ( I , II ))e Im S ( I ) Im S ( II ) 4 sin 2 ( (l d / 2))e 2 / H • The dS analog of Schwinger mechanism in QED: the correspondence between two accelerations (HawkingUnruh effect) qE H m RdS 12 Radiation in de Sitter Spaces • The Stokes phenomenon explains why there is NO particle production in odd dimensional de Sitter spaces - destructive interference between two Stokes’s lines -Polyakov intepreted this as reflectionless scattering of KdV equation [NPB797(2008)]. • In even dimensional de Sitter spaces, two Stokes lines contribute constructively, thus leading to de Sitter radiation. Vacuum Persistence • Consistent with the one-loop effective action from the in-/out-formalism in de Sitter spaces: -the imaginary part is absent/present in odd/even dimensions. 0, out | 0, in 2 e 2 ImW e VT ln(1 N k ) k • Does dS radiation imply the decay of vacuum energy of the Universe? -A solution for cosmological constant problem[Polyakov]. Can it work? Effective Action for Gravity • Charged scalar field in curved spacetime H ( x) 0, H ( x) D D m2 , D iqA ( x) • Effective action in the Schwinger-DeWitt proper time integral i 1 d W d x g d (is ) x | e isH | x' 0 2 (is ) im2 s 1 d e d x g d (is ) F ( x, x' ; is ) d /2 0 2 (is )( 4s) • One-loop corrections to gravity 1 1 2 1 1 ; f1 R, f 2 R; R R R R R 30 12 180 180 One-Loop Effective Action • The in-/out-state formalism [Schwinger (51), Nikishov (70), DeWitt (75), Ambjorn et al (83)] eiW e i dtd 3 xLeff 0, out | 0, in • The Bogoliubov transformation between the in-state and the out-state: ak,out k,in ak,in k,* inbk,in U k ak,inU k bk,out k,inbk,in k,* in ak, in U k bk,inU k One-Loop Effective Action • The effective action for boson/fermion [SPK, Lee, Yoon, PRD 78, 105013 (`08); PRD 82, 025015, 025016 (`10); ] W i ln 0, out | 0, in i ln k* k • Sum of all one-loops with even number of external gravitons Effective Action for de Sitter • de Sitter space with the metric 2 cosh ( Ht ) 2 2 2 ds dt d d H2 • Bogoliubov coefficients for a massive scalar (1 i )(i ) , lZ0 (l d / 2 i )(1 l d / 2 i ) (1 i )(i ) m2 d 2 l , 2 (l d / 2)(1 l d / 2) H 4 l Effective Action for dS [SPK, arXiv:1008.0577] • The Gamma-function Regularization and the Residue Theorem • The effective action per Hubble volume and per Compton time d 1 )mH d 2 Leff ( H ) (2 ) ( d 1) / 2 ( (d ) D l P 2 Im Leff ( H ) ln 1 N l , l 0 0 e s cos(( 2l d 1) s / 2) cos( s / 2) ds s sin( s / 2) sin (l d / 2) 2 N l | l | sinh( ) 2 Effective Action for de Sitter • The vacuum structure of de Sitter in the weak curvature limit (H<<m) R Leff ( RdS ) m 2 RdS Cn dS2 m n 0 n 1 • The general relation holds between vacuum persistence and mean number of produced pairs 0, out | 0, in 2 e2 Im Leff ( H ) exp (l 1) 2 ln(tanh 2 ( )) l 0 No Quantum Hair for dS Space? [SPK, arXiv:1008.0577] • The effective action per Hubble volume and per Compton time, for instance, in D=4 mH 3 Leff ( H ) (2 ) 2 (l 1) P 2 l 0 0 e s cos((l 1) s) cos( s / 2) ds s sin( s / 2) • Zeta-function regularization [Hawking, CMP 55 (1977)] 1 1 ( z ) z , (2n) 0, n Z , (0) 2 k 1 k Leff ( H ) 0 Effective Action of Spinor [W-Y.Pauchy Hwang, SPK, in preparation] • The Bogoliubov coefficients (1 / 2 im / H )(1 / 2 im / H ) j , (n j 1) , (1 / 2 im / H )(1 / 2 im / H ) (1 / 2 im / H )(1 / 2 im / H ) 1 0 j , jN 1 / 2 im / H ( )(1 ) 2 • The effective action Lsp eff ( H ) 2 (2 ) 2 mH 3 D j P j 2 Im L ( H ) ln 1 N j , sp eff 0 e ms / H sin 2 (s / 2) ds s sin( s / 2) sin N j | j | cosh( m / H ) 2 2 QED vs QG QED Schwinger Mechanism QCD Unruh Effect Pair Production Black holes Hawking Radiation De Sitter/ Expanding universe Conformal Anomaly, Black Holes and de Sitter Space Hawking temperature Black Holes Thermodynamics = Einstein Equation Jacobson, PRL (95) Bekenstein-Hawking entropy Conformal Anomaly ?? Hartle-Hawking temperature First Law of Thermodynamics = Friedmann Equation Cai, SPK, JHEP(05) Cosmological entropy Conformal Anomaly • An anomaly in QFT is a classical symmetry which is broken at the quantum level, such as the energy momentum tensor, which is conserved due to the Bianchi identity even in curved spacetimes. • The conformal anomaly is the anomaly under the 2 g e g conformal transformation: 2 2 T b1 F b2 ( E R) b3 2 R 3 E *R * R R R 4 R R R 2 F C C R R 2 R R 1 2 R 3 FLRW Universe and Conformal Anomaly • The FLRW universe with the metric 2 2 2 2 ds dt a (t )dx has the conformal Killing vector: Lt g ij 2 Hg ij • The FLRW metric in the conformal time 2 2 2 2 ds a ( )(d dx ) • The scale factor of the universe is just a conformal one, which leads to conformal anomaly. FLRW Universe and Conformal Anomaly • At the classical level, the QCD Lagrangian is conformally invariant for m=0: LQCD 1 a G Ga (i gTa Aa m) 4 • At the quantum level, the scale factor leads to the conformal anomaly [Crewther, PRL 28 (72)] ren T (g) 2 a G Ga ren (1 (m)) m ren • The FLRW universe leads to the QCD conformal anomaly [Schutzhold, PRL 89 (02)] T ren O( H3QCD ) 1029 g / cm3 0 Conformal Anomaly • The conformal anomaly from the nonperturbative renormalized effective action is 3 6 R H 2 Leff ( H ) C0 H 4 C2 2 C0 RdS C2 dS2 m m • The first term is too small to explain the dark energy at the present epoch; but it may be important in the very early stage of the universe even up to the Planckian regime. The trace anomaly may drive the inflation [Hawking, Hertog, Reall, PRD (01)]. Canonical QFT for Gravity • A free field has the Hamiltonian in Fourier-mode decomposition in FLRW universe d 3k H (t ) (2 )3 1 2 a 3k2 2 k , 3 k 2 2a 2 2 k 2 k m 2 a • The quantum theory is the Schrodinger equation and the vacuum energy density is [SPK et al, PRD 56(97); 62(00); 64(01); 65(02); 68(03); JHEP0412(04)] a 3 d 3k * 2 * H (t ) k k k k k 3 2 (2 ) Canonical QFT for Gravity • Assume an adiabatic expansion of the universe, which leads to k (t ) e i dt k / 2k a 3 • The vacuum energy density given by 1 d 3k 9H 2 9 H 3 [ k ] ( H cut off ) ( ) 3 2 2 (2 ) renormalization 8k 32 mB of bare Λ B is the same as by Schutzhold if H mB but the result is from nonequilibrium quantum field theory in FLRW universe. 1 d 3k 9 H 2 • Equation of state: p 3 2 H (2 ) 8k Conclusion • The effective action for gravity may provide a clue for the origin of . • Does dS radiation imply the decay of vacuum energy of the Universe? And is it a solver for cosmological constant problem? [Polyakov] • dS may not have a quantum hair at one-loop level and be stable for linear perturbations. • What is the vacuum structure at higher loops and/or with interactions? (challenging question)