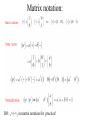* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download This course is: • Fun!
Bra–ket notation wikipedia , lookup
Quantum key distribution wikipedia , lookup
Wheeler's delayed choice experiment wikipedia , lookup
Density matrix wikipedia , lookup
Interpretations of quantum mechanics wikipedia , lookup
Renormalization group wikipedia , lookup
Elementary particle wikipedia , lookup
Wave–particle duality wikipedia , lookup
Particle in a box wikipedia , lookup
Dirac equation wikipedia , lookup
Bohr–Einstein debates wikipedia , lookup
Aharonov–Bohm effect wikipedia , lookup
History of quantum field theory wikipedia , lookup
Matter wave wikipedia , lookup
Electron configuration wikipedia , lookup
Atomic orbital wikipedia , lookup
Hidden variable theory wikipedia , lookup
Nitrogen-vacancy center wikipedia , lookup
Electron paramagnetic resonance wikipedia , lookup
Canonical quantization wikipedia , lookup
Ising model wikipedia , lookup
Wave function wikipedia , lookup
Quantum entanglement wikipedia , lookup
Probability amplitude wikipedia , lookup
Double-slit experiment wikipedia , lookup
Quantum electrodynamics wikipedia , lookup
Ferromagnetism wikipedia , lookup
Atomic theory wikipedia , lookup
Quantum state wikipedia , lookup
EPR paradox wikipedia , lookup
Bell's theorem wikipedia , lookup
Hydrogen atom wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Spin (physics) wikipedia , lookup
This course is:
• Fun!
– The ideas are presented in a way that makes a LOT more sense than a usual
QM course
– Focus on understanding one exemplar experiment in detail – you will
understand it well
– The simulation is pretty neat and allows you to relate the math to ‘real’
measurements
• Hard!
– New notation and language
– New math (hopefully not bad thanks to a great preface)
– Ideas that take some getting used to!
• Suggestions:
–
–
–
–
–
Make a vocabulary list – each bolded term in the text is a good place to start
Make a list of symbols and what they mean
Write the postulates in your own words with examples and explanations
Draw diagrams for any situation which is at first unclear to you
Do/repeat calculations to get practice
Goals:
• Understand the 6 postulates of quantum
mechanics (QM) and the nature of QM
• Proficiently use matrix mechanics in the context
of QM
• You will be able to solve 4 fundamental types of
problems – each done in detail within a specific
context, then generalized to any system:
– Sequential Stern-Gerlach measurements
• Analyze generic QM problems using matrix
mechanics
– Use time evolution to understand spin precession
• Analyze generic time dependent QM problems
using matrix mechanics
Postulates of QM
•What is a postulate?
•To assume or claim as true, existent, or necessary (from MerriamWebster)
•Tell us how to treat a QM system
•Successful and tested ideas
•Can not be proven
•Accepted as accurate but would need to be re-evaluated if new
results contradicted them
•6 main postulates
•Right now they have limited meaning
•Given so you know where we are headed and connect to preface
math
6 main postulates (and examples)
1.
2.
3.
4.
5.
6.
states are defined by kets: |+>, |->
Operators are matrices: H, S…
We measure eigenvalues: +/- h/2
Probability is found by: |<+|psi>|2
States “reduce” (collapse) |psi> goes to |+>
Schrodinger equation gives time evolution,
for instance, Larmor precession
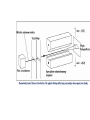
1.2 Stern-Gerlach experiment
Neutral silver atoms pass through a region of inhomogeneous
magnetic field
•Why silver? Why neutral?
•Why an inhomogeneous field?
Found two locations where the silver atoms ended up
•Why is this odd?
S
Ag
oven
Non uniform
B-field
N
magnet
screen
Ag: 1s2 2s2 2p6 3s2 3p6 4s2 3d10 4p6 4d10 5s1
Number of electrons 46
Angular momentum = ?
+
1
S
= 47
S-G historic overview
• They thought there should be splitting with the Bohr model
because
they thought that the silver atom should have a h/2pi
orbital angular
momentum from that model, when in fact it's zero
- L not zero, should see splitting (by S-G), and after much
effort,
they do and conclude Bohr is right
- but why splitting and not uniform if initial orientations
are
random? (Einstein and Ehrenfest)
- QM evolves, Bohr model found inadequate
- wait, L IS zero, why did they see splitting?
- then 5 years later, the idea of intrinsic spin...
Consider our expectations on what should happen to a neutral
particle in an inhomogeneous magnetic field:
•What does a magnetic field interact with?
•How can a neutral atom interact with a magnetic field?
•Let’s derive it classically from intro-course principles
•What does a simple magnetic dipole look like?
•What does the energy look like?
•What will the force be and why does the B need to be
inhomogeneous?
•How do we relate this to angular momentum?
•Why do we introduce “spin”?
•Does it really “spin”?
•What is different between what we expect to observe classically
and what we actually observe?
•What is a projection?
•What does two “spots” tell us about the spin?
•What is quantization?
“that” calculation
• More rigorous details posted on blackboard
• Found μ = (q/2m)L
• Have such a term for orbital angular momentum
L, “intrinsic spin” S, and for the total angular
momentum (the QM sum of L and S)
• Generalize: μ = g(q/2m)S
– S is the “intrinsic angular momentum” – as if the electron
spun on its axis, but NOT physical
– g is the gyromagntic/gyroscopic/g-ratio
– g is dimensionless
– g for electron is one of best known values in physics
What is “intrinsic spin”?
• Also called “spin”, or spin angular momentum, or S
• It’s a “degree of freedom”, or quantum number: a
“state” the particle has
• Does interact with magnetic fields like L, but not
continuous!
• NOT a physical rotation
• INTRINSIC property – like charge and rest mass!
We have no model for what “makes it up/causes it”
for fundamental particles
• Shows up most simply in Pauli exclusion principle
Stern-Gerlach Experiment 1
•What do we find here?
•First SG device is a “state preparation device” or “polarizer”
•2nd device is the “analyzer”
•How can we write the state vector out of the 1st device?
•Out of the 2nd device?
x
Z
0
Z
-x
-
0
0
Stern-Gerlach Experiment 2
What do we see?
If we do this one atom at a time, can we predict where it will end up?
What can we conclude about the relationship between the plus z state
and the x states?
Write a possible vector to show that relationship
LETS do the math for this – probabilities!
x
Z
0
X
-x
-
0
0
Stern-Gerlach Experiment 3
What do you expect to see?
TRY IT!
(a)
Z
X
x
Z
-
6 main postulates (and examples)
1.
2.
3.
4.
5.
6.
states are defined by kets: |+>, |->
Operators are matrices: H, S…
We measure eigenvalues: +/- h/2
Probability is found by: |<+|psi>|2
States “reduce” (collapse) |psi> goes to |+>
Schrodinger equation gives time evolution,
for instance, Larmor precession
Recap:
• Observe deflection of neutral atoms in
inhomogeneous magnetic field AS IF they had
angular momentum L:
– Except L is zero for those atoms – must be some other
“source” of angular momentum
– EXCEPT that instead of a continuous distribution of
deflection we get ONLY 2 “SPOTS” (“Quantization!”)
– Propose “S” = spin = intrinsic “angular momentum”
– Measuring the “strength” of that interaction (‘g’) is of
fundamental importance to particle physics research
– L and S can be combined quantum mechanically and
will be of importance to you later in your QM studies
Recap:
• S-G apparatus is how we look at the deflections –
the simulation is an easy way to make
“measurements” with successive S-G apparatuses at
different orientations
– Observe Z-Z measurement “prepares” the state with spin
along Z either “up” or “down”, and then “measures” the
state to still be as it was prepared
– Observe Z up and Z down (or X or Y) are orthonormal
– Observe Z-X (and Z-Y, and X-Y…) measurements and
find a probability that half the atoms with “spin up in Z”
(or down) will have “spin up in X” (or down)
– Postulate |+> = a|+>x + b|->x where a and b are complex,
a*a = b*b = ½, and a*a + b*b = 1
Conventions for “states”
• Can’t exactly specify the states, but have
“conventional” choices (details in text):
• (WRITE THESE ON THE BOARD!!)
• Row 1: write |+> and |-> in terms of |+>y and |->y
• Row 2: show that the |+>y and |->y states are
orthonormal
• Row 3: write |+>x in terms of |+>y and |->y
“Unexpected” observation:
• Saw that Z-X-Z did not “preserve” the spin up Z
states as spin up
• SAME thing happens with polarization of light!
This is not “bizarre” but is a property of a 2-state
system of this type
– Maybe: The S-G devise to analyze the spin states along
“X” must “alter” the state somehow (analogy with
polarizer – it “rotates” the polarization – or more
accurately the projection is non-zero
– Maybe: There is some effect from Heisenberg
Uncertainty
Z
X
Z
-
Calculations:
• ROW 1: Using our new knowledge about how to
write the spin states, calculate the probability that
a state initially with spin up along Z will have spin
up along Z after passing through a S-G devise for
analyzing the spin-X state (the “Z-X-Z” system)
• ROW 2: do the same for spin up along Z ending
up with spin down along Z
• ROW 3: do the same as ROW 1 except for the “ZY-Z” system
• (if you finish early work on another one!)
Stern-Gerlach Experiment 4
Consider what you found with the Z-X-Z system (shown in the top
figure) What do you expect to see if we combine the output beams
from both ports on the X devise, and put them into a Z?
TRY IT!
CALCULATE IT! What state are we putting into the last S-G device?
Z
X
Z
Z
-
x
X
-x
Z
-
Stern-Gerlach Experiment 4 - continued
• “you open the window further and let more sunlight
in yet the room gets darker!”
• Book discusses this by analogy with young’s double
slit interference experiment – what is the similarity?
z
electron beam
I1
F1
z
I
I I1 I 2
F2
I2
• We can also explain this effect using vector
addition, and by analogy with polarization vectors:
+
=
combination of states (“mixture”)
vs. superposition
• |+>x = (1/√2)[ |+> + |-> ]
• IF this meant half the atoms were in |+> and
half were in |->, what would we get if we
put this state into another S-G devise to
measure the spin along X?
• How do we know which we have in our S-G
system?
• (CALCULATE IT!)
Matrix notation:
DO: x<-|->y in matrix notation for practice!
Dirac:
• Who was P.A.M. Dirac?
– Paul Adrien Maurice Dirac (19021984)
– Studied general relativity and the then
brand new quantum mechanics
– Quote “In science one tries to tell
people, in such a way as to be
understood by everyone, something
that no one ever knew before. But in
poetry, it's the exact opposite”
– How did Dirac get his wife?
1.5 General Quantum Systems – more than 2 outcomes
Kronecker Delta: dij = {1, i = j
0, if i ≠ j }
so Σi dijai = aj
Summation: Σi bi|ai = b1|a1 + b2|a2 + b3|a3 + …
Where the b’s are complex, by convention b1 is real
Given: observable A – THIS IS A HERMITIAN MATRIX!
eigenvalues λn
eigenstates an
orthonormality
ai aj = dij
completeness
y = Si aiy ai = Si aiaiy
Si aiai = 1
Conjugation:
yf = fy*
General Quantum Systems
• Other 2-level systems:
– All fundamental fermions (leptons and quarks) are spin-1/2 systems
– Qubit (0 and 1 bit for quantum computing) candidates: 2 sets of
polarization pairs for photons, spin up and down of electron, electron’s
position in a quantum dot, atoms or ions either in spin states, or two
hyperfine (from intrinsic spin inside the nucleus) levels
• Other small-N-level systems:
– All baryons (like the proton) are composed of 3 spin-1/2 quarks, and
this can be spin 1/2, 3/2, …
– Bosons (force carriers) have integer spin: photon is spin 1, graviton (if
it exists) is spin 2
• Large/infinite-N systems: (usually represented by a wave
function)
– Finite quantum well
– Harmonic oscillator
Stern-Gerlach Experiment 4
What do you find as the output if you run all atoms through at once?
What do you find if you observe one atom at a time??
LOOK AT VIDEO FOR PHOTON ANALOG!
“Interference” is a property of states being SUPERPOSITIONS – NOT
mixtures
What do you think it means to “COLLAPSE” a state?? (postulate 5)
Z
x
X
-x
Z
-
Statistical Quantity Reminders
1
x=
N
Mean:
data
N
x
i =1
i
Number of data
Standard deviation: s =
1 N
2
x
x
=
i
N - 1 i =1
Standard deviation of the mean:
Probability:
P=
x
M
1 N 2
N 2
x
x
i
N - 1 i =1
N -1
s
m =
N
Number of atoms
Standard deviation of the probability:
p =
m
M