* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Bender
Quantum fiction wikipedia , lookup
Bohr–Einstein debates wikipedia , lookup
Measurement in quantum mechanics wikipedia , lookup
Identical particles wikipedia , lookup
Wave–particle duality wikipedia , lookup
Hydrogen atom wikipedia , lookup
Density matrix wikipedia , lookup
Quantum entanglement wikipedia , lookup
Particle in a box wikipedia , lookup
Quantum computing wikipedia , lookup
Many-worlds interpretation wikipedia , lookup
Matter wave wikipedia , lookup
Quantum machine learning wikipedia , lookup
Quantum group wikipedia , lookup
Bell's theorem wikipedia , lookup
Relativistic quantum mechanics wikipedia , lookup
Quantum teleportation wikipedia , lookup
Quantum key distribution wikipedia , lookup
Double-slit experiment wikipedia , lookup
History of quantum field theory wikipedia , lookup
Copenhagen interpretation wikipedia , lookup
Symmetry in quantum mechanics wikipedia , lookup
Coherent states wikipedia , lookup
EPR paradox wikipedia , lookup
Path integral formulation wikipedia , lookup
Interpretations of quantum mechanics wikipedia , lookup
Quantum state wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Quantum electrodynamics wikipedia , lookup
Hidden variable theory wikipedia , lookup
Canonical quantization wikipedia , lookup
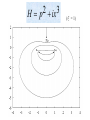
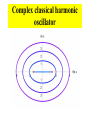
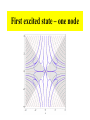
Complex Correspondence Principle Carl Bender Physics Department Washington University in collaboration with Daniel Hook Theoretical Physics Imperial College Extending quantum mechanics into the complex domain This Hamiltonian is PT symmetric Region of broken PT symmetry PT phase transition Region of unbroken PT symmetry The PT phase transition has now been seen experimentally! Laboratory verification using table-top optics experiments! Observing PT symmetry using optical wave guides: • Z. Musslimani, K. Makris, R. El-Ganainy, and D. Christodoulides, PRL 100, 030402 (2008) • K. Makris, R. El-Ganainy, D. Christodoulides, and Z. Musslimani, PRL 100, 103904 (2008) • A. Guo, G. J. Salamo, D. Duchesne, R. Morandotti, M. Volatier-Ravat, V. Aimez, G. A. Siviloglou, and D. N. Christodoulides, Phys. Rev. Lett. 103, 093902 (2009) The observed PT phase transition People at this meeting who have worked on PT quantum mechanics Thrust Cigar Moth Recalled Iran Hah! Minum Nipple Accuse Zinc Mule Bill to Milkman Mat Off John Mafia Had Zealts Nag Jck Jars Nth Loon Jag Verse Shh! Ask Veg Gnaw Knish (with apologies!) People at this meeting who have worked on PT quantum mechanics Thomas Curtright Andre LeClair Philip Mannheim Luca Mezincescu Kimball Milton John Moffat Ali Mostafazadeh Jack Ng John Ralston S G Rajeev K V Shajesh Kwang Shin (with apologies!) PT. There is a network that ties us together. Extending classical mechanics into the complex domain... Find all solutions, real or complex, to Hamilton’s equations: Motion on the real axis Motion of particles is governed by Newton’s Law: F=ma In freshman physics this motion is restricted to the REAL AXIS. Harmonic oscillator: Particle on a spring Back and forth motion on the real axis: Turning point Turning point Harmonic oscillator: Motion in the complex plane: Turning point Turning point The classical particle can enter the classically forbidden region! But its motion is orthogonal to the real axis! This is like total internal reflection: Glass Vacuum 2 3 H p ix ( = 1) 2 H = p - (ix) (11 sheets) Conventional correspondence principle Classical probability (1/speed) Quantum probability th 16 Eigenstate Complex classical harmonic oscillator Classical probability in the complex plane Pup Tent Complex quantum probability Potential is PT symmetric means Local conservation law: Probability contour Example: complex PTsymmetric random walk With a complex unfair coin! P(heads) = -ia + ½ P(tails) = ia + ½ Condition I Ground state of harmonic oscillator This equation looks easy, but it is impossible to solve exactly! Toy model Leading asymptotic behavior: Full asymptotic behavior: Where is the arbitrary constant?!? Difference of two solutions The arbitrary constant is in the hyperasymptotic contribution to the asymptotic approximation! Quantized bundle Separatrix Paths in the complex plane Bad Stokes’ wedge Good Stokes’ wedge Conditions II and III: Real part of the probability CONVERGENT!!! Going into and out of the bad Stokes’ wedge Probability contours in the complex plane More interesting contours... First excited state – one node Second excited state – two nodes This is the quantum version of the pup tent!! (with ripples on the canopy) These people are amazed that classical mechanics and quantum mechanics can be extended into the complex plane, and that the correspondence principle continues to hold!