Download UNIT 2-RATIONAL NUMBERS

MATHEMATICS
GRADE 7
UNIT 2
RATIONAL NUMBERS
GRADE 7 • MODULE 2
RATIONA L NUMBERS
OVERVIEW
In Grade 6, students formed a conceptual understanding of integers through the use of the number line, absolute value,
and opposites and extended their understanding to include the ordering and comparing of rational numbers (6.NS.C.5,
6.NS.C.6, 6.NS.C.7). This module uses the Integer Game: a card game that creates a conceptual understanding of
integer operations and serves as a powerful mental model students can rely on during the module. Students build on
their understanding of rational numbers to add, subtract, multiply, and divide signed numbers. Previous work in
computing the sums, differences, products, and quotients of fractions serves as a significant foundation as well.
In Topic A, students return to the number line to model the addition and subtraction of integers (7.NS.A.1). They use
the number line and the Integer Game to demonstrate that an integer added to its opposite equals zero, representing
the additive inverse (7.NS.A.1a, 7.NS.A.1b). Their findings are formalized as students develop rules for adding and
subtracting integers, and they recognize that subtracting a number is the same as adding its opposite (7.NS.A.1c). Reallife situations are represented by the sums and differences of signed numbers. Students extend integer rules to include
the rational numbers and use properties of operations to perform rational number calculations without the use of a
calculator (7.NS.A.1d).
Students develop the rules for multiplying and dividing signed numbers in Topic B. They use the properties of
operations and their previous understanding of multiplication as repeated addition to represent the multiplication of a
negative number as repeated subtraction (7.NS.A.2a). Students make analogies to the Integer Game to understand that
the product of two negative numbers is a positive number. From earlier grades, they recognize division as the inverse
process of multiplication. Thus, signed number rules for division are consistent with those for multiplication, provided a
divisor is not zero (7.NS.A.2b). Students represent the division of two integers as a fraction, extending product and
quotient rules to all rational numbers. They realize that any rational number in fractional form can be represented as a
decimal that either terminates in 0s or repeats (7.NS.A.2d). Students recognize that the context of a situation often
determines the most appropriate form of a rational number, and they use long division, place value, and equivalent
fractions to fluently convert between these fraction and decimal forms. Topic B concludes with students multiplying and
dividing rational numbers using the properties of operations (7.NS.A.2c).
In Topic C, students problem-solve with rational numbers and draw upon their work from Grade 6 with expressions and
equations (6.EE.A.2, 6.EE.A.3, 6.EE.A.4, 6.EE.B.5, 6.EE.B.6, 6.EE.B.7). They perform operations with rational numbers
(7.NS.A.3), incorporating them into algebraic expressions and equations. They represent and evaluate expressions in
multiple forms, demonstrating how quantities are related (7.EE.A.2). The Integer Game is revisited as students discover
“if-then” statements, relating changes in player’s hands (who have the same card-value totals) to changes in both sides
of a number sentence. Students translate word problems into algebraic equations and become proficient at solving
equations of the form 𝑝𝑥 + 𝑞 = 𝑟 and 𝑝(𝑥 + 𝑞) = 𝑟, where 𝑝, 𝑞, and 𝑟, are specific rational numbers (7.EE.B.4a). As
they become fluent in generating algebraic solutions, students identify the operations, inverse operations, and order of
steps, comparing these to an arithmetic solution. Use of algebra to represent contextual problems continues in Module
3.
This module is comprised of 23 lessons; 7 days are reserved for administering the Mid- and End-of-Module Assessments,
returning the assessments, and remediating or providing further applications of the concepts. The Mid-Module
Assessment follows Topic B, and the End-of-Module Assessment follows Topic C.
2
VOCABULARY FOR FLASHCARDS
A.) Absolute Value: The absolute value of a number represents the
positive distance the number is away from the
origin (0). The symbol: x is used when the
absolute value of a number needs to be found.
B.) Additive Identity: The additive identity is 0.
C.) Additive Inverse: The additive inverse of a real number is the opposite
of that number on the real number line. For example,
the opposite of –3 is 3. A number and its additive
inverse have the sum of 0.
D.) Algebraic Equation: An algebraic equation is a collection of
numbers, variables, operations, and grouping
of symbols while using an equal sign.
Example 1:
Example 2:
Example 3:
Example 4:
Example 5:
a + b = 10
2a – 5 = 7
3abc = 100
a + a + b + b = 2a + 2b
3a = a + a + a
E.) Algebraic Expression: An algebraic expression is a collection of
numbers, variables, operations, and grouping
of symbols without using an equal sign.
Example 1:
Example 2:
Example 3:
Example 4:
Example 5:
a+b
2a -5 + c
3abc
(ab) – (cd) + 5
a+5
3
F.) Distance Formula: If p and q are rational numbers on a number line,
then the distance between p and q is |𝒑 − 𝒒|.
G.) Evaluating: Evaluating is when the variable(s) in an expression, equation or inequality
is/are replaced with a number and then a numerical answer is found.
H.) Inverse Operations: The use of inverse operations are essential in the topic of Algebra.
Inverse operations allows the mathematician to solve for an
unknown variable. The use of inverse operations is the undoing of
the operation being worked with.
Example 1:
Example 2:
Example 3:
Example 4:
The inverse operation of addition is subtraction.
The inverse operation of subtraction is addition.
The inverse operation of division is multiplication.
The inverse operation of multiplication is division.
I.) Irrational Numbers: A number is irrational if it can’t be written
as a fraction with an integer numerator and a
nonzero integer denominator.
*AN EASY WAY TO REMEMBER IRRATIONAL NUMBERS*
*An irrational number is a nonrepeating/nonterminating decimal (never
ends!!!!!)
*Three Major Categories We Study Are:
1) pi: 
2) Non-Perfect Square Roots:
3, 5, 6, 7,...
3) Decimals (Non-Terminating and Non-Repeating): 7.123145…,
.03003000300003000003…
J.) Multiplicative Identity: The multiplicative identity is 1.
4
K.) Rational Numbers: A number is rational if it can be written as a
fraction with an integer numerator and a
nonzero integer denominator.
Examples: 0.4, 2.9, 16 , 0.3, 0.6
5
TERMINOLGY
1.) Additive Identity: The additive identity is 0.
2.) Additive Inverse: The additive inverse of a real number is the opposite
of that number on the real number line. For example, the opposite of -3
is 3. A number and its additive inverse have the sum of 0.
3.) Break-Even Point: The point at which there is neither a profit nor loss.
4.) Distance Formula: If p and q are rational numbers on a number line,
then the distance between p and q is |𝒑 − 𝒒|.
5.) Loss: A decrease in the amount; as when the money earned is less than
the money spent.
6.) Multiplicative Identity: The multiplicative identity is 1.
7.) Profit: A gain, as in the positive amount represented by the difference
between the money earned and spent.
8.) Repeating Decimal: The decimal form of a rational number, for example
𝟏
̅.
= 𝟎. 𝟑
𝟑
9.) Terminating Decimal: A decimal is called terminating if it is repeating
digit is 0.
6
Subsets of Real Numbers
A. Counting Numbers or Natural Numbers: 1, 2, 3, 4, 5, …..
B. Whole Numbers: 0, 1, 2, 3, 4, 5, …..
C. Integers: (negative infinity)  ,..., 3, 2, 1,0,1, 2,3,.....,  (infinity)
D. Rational Numbers: A number is rational if it can be written as a
fraction with an integer numerator and a
nonzero integer denominator.
Examples: 0.4, 2.9, 16 , 0.3, 0.6
E. Irrational Numbers: A number is irrational if it cannot be written
as a fraction with an integer numerator and a
nonzero integer denominator.
Examples:  
3.141592654…..
2 
1.414213562…..
3 
1.732050808…..
*AN EASY WAY TO REMEMBER IRRATIONAL NUMBERS*
*An irrational number is a nonrepeating/nonterminating decimal (never
ends!!!!!)
*Three Major Categories We Study Are:
1) pi: 
2) Non-Perfect Square Roots:
3, 5, 6, 7,...
3) Decimals (Non-Terminating and Non-Repeating): 7.123145…,
.03003000300003000003…
7
Integers
In the world of mathematics, there are many types of numbers. In this chapter, we are going
to be talking about a particular family of numbers that has been discussed before. These
numbers are called integers. Let us review what they look like:
(negative infinity)  ,....., 5, 4, 3, 2, 1,0,1, 2,3, 4,5,..... (infinity)
Integers on a number line look like this:
smaller
negative numbers
larger
zero
positive numbers
*When negative numbers are written, the symbol (-) is placed before the
number.
Example 1:
Example 2:


3 is read as: “negative three”
5.9 is read as: “negative five point nine” or
“negative five and nine tenths”
F. Opposite Number: The value of -5 and 5 on the graph below are an
equal distance from each other. These are called
opposite numbers. The reason for this is
because the two values are equal distance from
the origin (0).
8
G. Absolute Value: The absolute value of a number represents the
positive distance the number is away from the
origin (0). The symbol: x is used when the
absolute value of a number needs to be found.
Example 1: 2 = 2
Example 2:  2 = 2
Example 3: 0 = 0
Example 4:
Example 5:   2 =  2
Example 6:

2 = 2

62
6-2
4
Example 7:  7  3

7–3
-10
Example 8:
Example 9: 0   2
Example 10:

8  9
8+9
17
 2

2
0–2

2
4
9
2
2
H. Additive Inverse(Opposite): A number and its opposite have a sum of zero.
Example 1: g + (-g) = 0
Example 2: 5 + (-5) = 0
Example 3:
1  1 
   0
2  2 
I. Addition Property of Zero: A number added to zero leaves the
number unchanged.
Example 1: g + 0 = g
Example 2: 5 + 0 = 5
Example 3:
1
1
0 
2
2
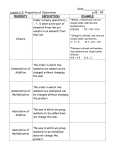
J. Commutative Property: Addition and Multiplication
PLEASE NOTE: CHANGE IN ORDER
Example 1: x + y = y + x
Example 2: 3 + 8 = 8 + 3
Example 3: x • y = y • x
Example 4:
3 1 1 3
  
4 3 3 4
K. Associative Property: Addition and Multiplication
PLEASE NOTE: CHANGE IN GROUPING
Example 1: a + (b + c) = (a + b) + c
Example 2: 4 + (6 + 7) = (4 + 6) + 7
Example 3: a • (b • c) = (a • b) • c
Example 4: 2 x (3 x 4) = (2 x 3) x 4
10
L. Polynomial: A polynomial is an expression that has a sum or
difference of one or more terms.
M. Algebraic Expression: An algebraic expression is a collection of
numbers, variables, operations, and
grouping of symbols without using an equal
sign.
Example 1: a + b
Example 2: 2a -5 + c
Example 3: 3abc
Example 4: (ab) – (cd) + 5
Example 5: a + 5
N. Terms: Terms are the parts that are added or subtracted in a
mathematical expression.
axn
a: represents any real number (any number we have used this year)
x: represents the variable being used but could be any letter (c, d, m, r, ...)
n: is an exponent/power that is a whole number (0, 1, 2, 3, 4, …)
Examples of Polynomials
Name
Number of Terms
Examples
Monomial
1
x, -3a, 3, 5y, 0.5c,
Binomial
2
3a – 5, b2 + 9b
Trinomial
3
x2 – 6x + 7, 4c2 + c - 2
*Please Note: There can be polynomials with four or more terms.
11
O. Distributive Property of Multiplication Over Addition and
Subtraction
1) Distributive Property of Multiplication Over Addition(“sum of”):
a(b + c) = ab + ac
OR
ab + ac = a(b + c)
2) Distributive Property or Multiplication Over
Subtraction(“difference of”):
a(b – c) = ab – ac
OR
ab – ac = a(b - c)
HOW THE DISTRIBUTIVE PROPERTY CAN BE USED
FINDING PRODUCTS
Example 1: 4(3 + 2) = (4 x 3) + (4 x 2) = 12 + 8 = 20
Example 2: 2(8 – 3) = (2 x 8) – (2 x 3) = 16 – 6 = 10
Example 3: 9 x 27 = (9 x 20) + (9 x 7) = 180 + 63 = 243
Example 4: 5
1
x6=
2
1
1

 5   6 = (5 x 6) + ( x 6) = 30 + 3 = 33
2
2

Example 5: 4 x 29 = (4 x 30) – (4 x 1) = 120 – 4 = 116
Example 6: 7 x 102 = (7 x 100) + (7 x 2) = 700 + 14 = 714
Example 7: 3.5 x 20 = (3 + .5)20 = (3 x 20) + (.5 x 20) = 60 + 10 = 70
CHANGING THE FORM OF AN ALGEGRAIC EXPRESSION
Example 1: 8(x + y) = 8x + 8y
Example 2: 3.4(a – b) = 3.4a – 3.4b
Example 3:
1
1
1
(9 x  6 x)  (  9 x   6 x)  4.5 x  3 x  1.5 x
2
2
2
12
USING THE NUMBER LINE TO MODEL ADDITION OF INTEGERS
Example 1: -4 + 9
Example 2: -5 + -2
Example 3: 8 + -13
FINAL THOUGHT:
A.) ADD POSITIVE INTEGERS BY COUNTING UP/RIGHT.
B.) ADD NEGATIVE INTEGERS BY COUNTING DOWN/LEFT.
C.) ON A NUMBER LINE, ARROWS ARE USED TO REPRESENT
INTEGERS, THEY SHOW LENGTH AND DIRECTION.
D.) THE LENGTH OF AN ARROW ON THE NUMBER LINE IS THE
ABSOLUTE VALUE OF THE INTEGER.
E.) THE SUM OF SEVERAL ARROWS IS THEF FINAL POSITION
OF THE LAST ARROW.
13
ADDITION OF RATIONAL NUMBERS
A. Adding Two Rational Numbers: 2 Situations
Situation 1: SAME SIGNS
{“SAME SIGNS, FIND SUM OF ABSOLUTE VALUES, KEEP SIGN”}
Rule: Add the absolute value of each number and keep the sign
Example 1: 4 + 2 = ?
4 4
2 2
Therefore: 4 + 2 = 6
ANSWER IS POSITIVE BECAUSE SIGN OF ORIGINAL NUMBERS ARE POSITIVE
Example 2:

2 2

3 3

2 + 3 = ?
Therefore:  2 +  3 =  5
THE ANSWER IS NEGATIVE BECAUSE THE SIGN OF ORIGINAL NUMBERS ARE
NEGATIVE
Example 3: -3x + -5x = ?

3x  3x

5x  5x
Therefore: -3x + -5x = -8x
THE ANSWER IS NEGATIVE BECAUSE THE SIGN OF ORIGINAL NUMBERS ARE
NEGATIVE
14
Situation 2: DIFFERENT SIGNS
{“FIND THE DIFFERENCE OF ABSOLUTE VALUES, KEEP SIGN OF HIGHER
ORIGINAL ABSOLUTE VALUE”}
Rule:
1. Take absolute value of each number
2. Subtract the smaller absolute value from the bigger absolute value
3. The sign of the original number with the larger absolute value will be
the sign of the answer
Example 1:


4x + 2x = ?
4x = 4x
2x = 2x
4x – 2x = 2x
Therefore:  4 x  2 x   2 x FINAL ANSWER IS NEGATIVE BECAUSE  4x HAS A
LARGER ABSOLUTE VALUE
Example 2: 8 +  3 = ?
8 =8

3 =3
8–3=5
Therefore: 8 +  3 = 5 FINAL ANSWER IS POSITIVE BECAUSE 8 HAS A LARGER
ABSOLUTE VALUE
Example 3:
1 
 5?
2
1
1
=
2
2
5 = 5
5-
1
10 1
9
1
= - = 4
2
2 2
2
2
Therefore:
1 
1
 5  4
FINAL ANSWER IS NEGATIVE BECAUSE
2
2
-5 HAS A LARGER ABSOLUTE VALUE
15
SUBTRACTION OF RATIONAL NUMBERS
Rule:
1. Follow addition rules
2. Change signs only with double negatives
DOUBLE NEGATIVES BECOME POSITIVE
Example 1: 4 – 8 = ?
4 4
8  8
8–4=4
Therefore: 4 – 8 =  4 FINAL ANSWER IS NEGATIVE BECAUSE -8 HAS A LARGER
ABSOLUTE VALUE
Example 2: 4 -  4 = ? EXAMPLE OF DOUBLE NEGATIVES
REWRITE: 4 + 4 = ?
4 4
4 4
4+4=8
Therefore: 4 -  4 = 8 FINAL ANSWER IS POSITIVE BECAUSE THE SIGNS ARE
THE SAME
Example 3: -6p – 14p = ?
6 p  6 p
14 p  14 p
6p + 14p = 20p
Therefore: -6p – 14p = -20p FINAL ANSWER IS NEGATIVE BECAUSE THE SIGNS
ARE THE SAME
16
THE DISTANCE BETWEEN TWO RATIONAL NUMBERS
Example 1: What is the distance between 3 and 8?
|𝟑 − 𝟖| = |−𝟓| = 𝟓
Example 2: What is the distance between -3 and 8?
|−𝟑 − 𝟖| = |−𝟏𝟏| = 𝟏𝟏
Example 3: What is the distance between 10 and -6?
|𝟏𝟎 − (−𝟔)| = |𝟏𝟎 + 𝟔| = 𝟏𝟔
FINAL THOUGHTS:
1.) TO FIND THE DISTANCE BETWEEN TWO RATIONAL NUMBERS ON A
NUMBER LINE, YOU CAN COUNT THE NUMBER OF UNITS BETWEEN
THE NUMBERS.
2.) USING A FORMULA, THE DISTANCE BETWEEN RATIONAL NUMBERS,
p and q, IS |𝒑 − 𝒒|.
3.) DISTANCE IS ALWAYS POSITIVE.
4.) CHANGE MAY BE POSITIVE OR NEGATIVE. FOR EXAMPLE, THERE IS
-4O CHANGE WHEN THE TEMPERATURE GOES FROM 7O TO 3O.
17
DIVISION AND MULTIPLICATION OF RATIONAL
NUMBERS
Rule 1: Even number of negatives will result in a positive answer
Rule 2: Odd number of negatives will result in a negative answer
PLEASE NOTE: RULES FOR DIVISION AND MULTIPLICATION OF RATIONAL
NUMBERS ARE THE SAME!
Example 1: 5 x 5 = 25 (no negative signs)
Example 2:

3 x 9 =  27 (one negative sign)
Example 3:

4 x 4 =  16 (one negative sign)
Example 4:

8 x  2 = 16 (two negative signs)

Example 5:
4 x 3 x 2 =  24 (one negative sign)
Example 6: -2 x  3 x 2 = 12 (two negative sign)
Example 7:

1 x  2 x 3 x 2 x  4 =  48 (three negative signs)
MULTIPLYING FRACTIONS AND INTEGERS: NO
CALCULATOR, NO PROBLEM!!!!!
Example 8:
2
 15 IS THE SAME AS:
3
“2 MULTIPLIED BY 15 DIVIDED BY 3” OR
“15 DIVIDED BY 3 MULTIPLIED BY 2”
ANSWER: 10
Example 9:
3
(10 x ) IS THE SAME AS:
5
“3 MULTIPLIED BY 10x DIVIDED BY 5” OR
“10x DIVIDED BY 5 MULTIPLIED BY 3”
ANSWER: 6x
18
Different Variations of Multiplication Forms
a) A dot can be used: 3  6 = 18
(2.1)  4 = 8.4
b) Two parenthesis next to each other with numbers inside: (3)(6) = 18
c) Two or more variables next to each other: ab or xyz
Example 10:
Example 11:
Example 12:
8
= 4 (no negative signs)
2
7
1

9
 3 (no negative signs)
3

Example 13:
Example 14:
=  7 (one negative sign)

8
 4 (two negative signs)
2
0
 0 (no negative signs)
2
10
10 2 5
2
Example 15: 9     1 (no negative signs)
2
9 3 3
3
3

4

4 3 4 13 4 1  2 1 2
26
Example 16:
(one negative sign)

 
 
 
 
3
26 13 26 3
2 3 1 3 3
13
Please Remember: It is impossible to divide by zero, the answer is
called “undefined.”
Examples 15: 7  0 = undefined
Example 16: 0 7 = undefined
Example 17: 0  0 = undefined
19
WRITING OF NEGATIVE SIGN WITH DIVISION
 p   p
p
  

q
 q 
q
1
 1   1
  

3
 3
3
a
 a   a 
  

4
 4 
4
7
 7   7 
  

9
 9 
9
20
CHANGING DECIMALS TO FRACTIONS OR MIXED NUMBERS
METHOD OF CHANGING DECIMALS TO FRACTIONS
1. Determine the place value the terminating decimal ends.
2. Write the decimal part over the place holder and simplify.
PLEASE NOTE: IF A NUMBER APPEARS TO THE LEFT OF THE DECIMAL,
WRITE IT NEXT TO THE SIMPLIFIED FRACTION AND IT WILL RESULT
IN A MIXED NUMBER.
Example 1: 0.215
𝟐𝟏𝟓
𝟒𝟑
=
𝟏𝟎𝟎𝟎
𝟐𝟎𝟎
Example 2: 2.35
𝟑𝟓
𝟏𝟎𝟎
2
=
𝟕
𝟐𝟎
𝟕
𝟐𝟎
CONVERTING FRACTIONS TO DECIMALS-FRACTIONS WITH
DENOMINATORS HAVING FACTORS OF ONLY 2 AND/OR 5
Example: Write the number
𝟕
𝟐𝟎
=
𝟕
𝟐𝟐 •𝟓
𝟕
𝟐𝟎
as a decimal without a calculator.
The denominator needs a factor of 5 to be a power of 10.
Multiply both the numerator and denominator by 5 to arrive at
decimal form is 0.35
𝟑𝟓
𝟏𝟎𝟎
. The
FINAL THOUGHT: ANY TERMINATING DECIMAL CAN BE CONVERTED TO
A FRACTION USING PLACE VALUE. A FRACTION WHOSE DENOMINATOR
INCLUDES ONLY FACTORS FO 2 AND 5 CAN BE CONVERTED TO A
DECIMAL BY WRITING THE DENOMINATOR AS A POWER OF TEN.
21
CHANGING PERCENTS TO FRACTIONS
METHOD OF CHANGING PERCENTS TO FRACTIONS:
1. Write the percent over 100 (percent means per 100)
2. Simplify if asked
Example 1: 𝟖% =
𝟖
𝟏𝟎𝟎
Example 2: 𝟐𝟏𝟎% =
𝟐𝟓
𝟐𝟏𝟎
𝟏𝟎𝟎
𝟏
𝟑
𝟏
𝟑
𝟑
𝟏𝟎𝟎
Example 3: 𝟑 % =
𝟐
=
=
=
𝟐𝟏
𝟏𝟎
𝟏𝟎
𝟑
•
=𝟐
𝟏
𝟏𝟎𝟎
𝟏
𝟏𝟎
=
𝟏
𝟑𝟎
CHANGING PERCENTS TO DECIMALS
METHOD OF CHANGING PERCENTS TO DECIMALS
1. Move the decimal point two places to the left (means dividing by 100)
Example 1: 90% = .9
Example 2: 0.2% = 0.002
𝟏
̅
Example 3: 𝟑 % = 𝟎. 𝟎𝟑
𝟑
Example 4: 5% = 0.05
22
CHANGING DECIMALS TO PERCENT
METHOD OF CHANGING DECIMALS TO PERCENTS:
1. Move the decimal point two places to the right (means multiplying by 100)
Example 1: 0.8 = 8%
Example 2: 1.95 = 195%
Example 3: 1 = 100%
Example 4: 0.089 = 8.9%
CHANGING FRACTIONS TO PERCENTS
METHOD OF CHANGING FRACTIONS TO PERCENTS:
1. Convert the fraction to a decimal (numerator divided by the denominator)
2. Move the decimal point two places to the right (means multiplying by 100)
Example 1:
𝟑
Example 2:
𝟏
Example 3:
Example 4:
= 𝟎. 𝟕𝟓 = 𝟕𝟓%
𝟒
̅ = 𝟑𝟑. 𝟑
̅%
= 𝟎. 𝟑
𝟑
𝟖
𝟑𝟐
= 𝟎. 𝟐𝟓 = 𝟐𝟓%
𝟏𝟐𝟎
𝟓
= 𝟐𝟒 = 𝟐𝟒𝟎𝟎%
23
CONVERTING A RATIONAL NUMBER TO A DECIMAL
USING LONG DIVISION
Procedure: Long division has basically 4 steps.
Step 1:
Step 2:
Step 3:
Step 4:
Divide
Multiply
Subtract
Drop down next digit
REPEAT STEPS 1 – 4 UNTIL THE DECIMAL FORM OF A RATIONAL NUMBER
TERMINATES IN 0’S OR REPEATS
HELPFUL TIP
STARTING WITH A FRACTION IN LOWEST TERMS, IF THE DENOMINATOR
HAS A PRIME FACTOR OTHER THAN 2 OR 5, THEN THE DECIMAL FORM OF
THE NUMBER WILL BE REPEATING
Example 1:
1.363
11 15.000
-11
40
-33
70
-66
40
-33
7
15
11
ANSWER = 1.36
*The decimal repeats and could have been determined before division
because the denominator 11 is a prime factor other than 2 or 5.
24
Algebra Terms
A. Algebraic Equation: An algebraic equation is a collection of
numbers, variables, operations, and grouping
of symbols while using an equal sign.
Example 1:
Example 2:
Example 3:
Example 4:
Example 5:
a + b = 10
2a – 5 = 7
3abc = 100
a + a + b + b = 2a + 2b
3a = a + a + a
B. Algebraic Expression: An algebraic expression is a collection of
numbers, variables, operations, and grouping
of symbols without using an equal sign.
Example 1:
Example 2:
Example 3:
Example 4:
Example 5:
a+b
2a -5 + c
3abc
(ab) – (cd) + 5
a+5
C. Coefficient: When a constant and variables are factors of a product,
the constant is the number that is in front. This is called the coefficient.
D. Evaluating: Evaluating is when the variable(s) in an expression, equation or inequality
is/are replaced with a number and then a numerical answer is found.
E. Factor: If two or more numbers are to be multiplied, each of the numbers, as well as the
product of any of them is called a factor. A factor may involve variables also.
25
F. Inverse Operations: The use of inverse operations are essential in the topic of Algebra.
Inverse operations allows the mathematician to solve for an
unknown variable. The use of inverse operations is the undoing of
the operation being worked with.
Example 1: The inverse operation of addition is subtraction.
Example 2: The inverse operation of subtraction is addition.
Example 3: The inverse operation of division is multiplication.
Example 4: The inverse operation of multiplication is division.
26
G. Polynomial: A polynomial is an expression that can be formed from a variable and
numerical coefficients, using only the operations of addition, subtraction, and
multiplication. The variable is never in the denominator of a fraction. All
exponents of the variable must be positive integers.
axn
a: represents any real number (any number we have used this year)
x: represents the variable being used but could be any letter (c, d, m, r, ...)
n: is an exponent/power that is a whole number (1, 2, 3, 4, …)
Terms: Terms are the parts that are added or subtracted in a polynomial. Also, terms are the
parts that make up an expression, equation or inequality. Examples: 2, 5a, c, -7c,
ab, ….. Terms that are (like or same) can be combined together.
Examples of Polynomials
Name
Number of Terms
Examples
Monomial
1
x, -3a, 3, 5y, 0.5c,
Binomial
2
3a2 – 5, b2 + 9b
Trinomial
3
x2 – 6x + 7, 4c2 + c - 2
*Please Note: There can be polynomials with four or more terms.
H. Tape Diagrams: A tape diagram can be used to model and identify the sequence of
operations to find a solution algebraically.
I. Substitution: Substitution is when the variable(s) in an expression,
equation, or inequality is/are replaced with a number.
J. Variable: A variable is a letter that is used to represent one or more
numbers.
K. Values: The numbers that represent variables are called values.
27
Distributive Property of Multiplication Over Addition and Subtraction
1) Distributive Property of Multiplication Over Addition(“sum of”):
a(b + c) = ab + ac
OR
ab + ac = a(b + c)
2) Distributive Property or Multiplication Over Subtraction(“difference of”):
a(b – c) = ab – ac
OR
ab – ac = a(b - c)
HOW THE DISTRIBUTIVE PROPERTY CAN BE USED
FINDING PRODUCTS
Example 1: 4(3 + 2) = (4 x 3) + (4 x 2) = 12 + 8 = 20
Example 2: 2(8 – 3) = (2 x 8) – (2 x 3) = 16 – 6 = 10
Example 3: 9 x 27 = (9 x 20) + (9 x 7) = 180 + 63 = 243
Example 4: 5
1
x6=
2
1
1

 5   6 = (5 x 6) + ( 2 x 6) = 30 + 3 = 33
2

Example 5: 4 x 29 = (4 x 30) – (4 x 1) = 120 – 4 = 116
Example 6: 7 x 102 = (7 x 100) + (7 x 2) = 700 + 14 = 714
Example 7: 3.5 x 20 = (3 + .5)20 = (3 x 20) + (.5 x 20) = 60 + 10 = 70
CHANGING THE FORM OF AN ALGEGRAIC EXPRESSION
Example 1: 8(x + y) = 8x + 8y
Example 2: 3.4(a – b) = 3.4a – 3.4b
Example 3:
1
1
1
(9 x  6 x)  (  9 x   6 x)  4.5 x  3 x  1.5 x
2
2
2
28
EVALUATING VARIABLE EXPRESSION INVOLVING THE DISTRIBUTIVE
PROPERTY
1A. Simplify the variable expression.
-2(x – 7y) + 3(2x – 2y)
-2x + 14y + 6x - 6y
4x + 10y
1B. Using Part A, evaluate when x = 2 and y = -3.
4x + 8y
4(2) + 8(-3)
8 – 24
-16
SIMPLIFYING VARIABLE EXPRESSIONS
1. 5x + 15 – 10
2. 3(2 – 3c) + 5c
6 – 9c + 5c
6 – 4c
5x + 5
3. 9 – (5r + 7)
4. 7x – 4y – 2(5x + 6y)
9 – 5r – 7
2 – 5r
5.

7x – 4y - 10x – 12y
-3x – 16y


2
2
14 x 2  21  40 x 2  25
7
5

6.



4 3
2
x 100 x 2  20  x 9 x 2  6
5
3
4 x 2  6  16 x 2  10
80 x 5  16 x 3  6 x 3  4
 10 x 2  4
80 x 5  10 x 3  4
29

SIMPLIFYING VARIABLE EXPRESSIONS CONTINUED
1
3
1
1
7.  2 x    1 x  
 3
4  2
3
1
1
3 1
2 x 1 x  
3
2
4 3
1
2
8
2 x  2 x 1 x
3
6
6
1
2
3
6
3
6
5
x
6
- 1 x  1 x  1 x
3 9

4 12
1
3
+ 
Answer =
30
4
12
13
1
1
12
12
5
1
x 1
6
2
One Step Equations
Method:
1. Simplify the left side of the equal sign (if possible).
2. Simplify the right side of the equal sign (if possible).
Please Note: When simplifying, this could involve combining like
terms, distributive property, etc.
a) Distributive Property of Multiplication over Addition:
a(b + c) = ab + ac
b) Distributive Property of Multiplication over Subtraction:
a(b – c) = ab – ac
3. Gather all variables to one side of the equal sign by using
inverse operations.
4. Gather all constants to the opposite side of the variables by using inverse operations.
5. Isolate (get by itself) the variable by using inverse operations.
6. Check
*substitute solution into original equation
*perform steps for order of operations
Examples
1. a + 5 = 10
- 5 -5
a
= 5
Check
a + 5 = 10
(5) + 5 = 10
10 = 10
Check
3. x – 7 = -10
x – 7 = -10
+7
+7 (-3) – 7 = -10
x
= -3
-10 = -10
2. b + 1.2 = 3.7
- 1.2 -1.2
b
= 2.5
Check
b + 1.2 = 3.7
(2.5) + 1.2 = 3.7
3.7
= 3.7
Check
4. b – 7.98 = 9.00
b – 7.98 = 9.00
+ 7.98 +7.98 (16.98) – 7.98 = 9.00
b
= 16.98
9.00
= 9.00
31
One Step Equations Continued
3a 12

5.
3 3
a = -4
Check
-3a = 12
-3(-4) = 12
12 = 12
Check
6. d  5.5 = 33
d
x 5.5 x 5.5
= 181.5
32
d  5.5 = 33
(181.5)  5.5 = 33
33
= 33
Two-Step Equations
Method:
1. Simplify the left side of the equal sign (if possible).
2. Simplify the right side of the equal sign (if possible).
Please Note: When simplifying, this could involve combining like
terms, distributive property, etc.
a) Distributive Property of Multiplication over Addition:
a(b + c) = ab + ac
b) Distributive Property of Multiplication over Subtraction:
a(b – c) = ab – ac
3. Gather all variables to one side of the equal sign by using
inverse operations.
4. Gather all constants to the opposite side of the variables by using inverse operations.
5. Isolate (get by itself) the variable by using inverse operations.
6. Check
*substitute solution into original equation
*perform steps for order of operations
Examples
1. 2x + 6 =12
- 6 -6
2x 6

2 2
Check
2x + 6 = 12
2(3) + 6 = 12
6
+ 6 = 12
12 = 12
2. 3y – 12 = 9
+ 12 +12
3 y 21

3
3
y = 7
x=3
33
Check
3y – 12 = 9
3(7) – 12 = 9
21 – 12 = 9
9
= 9
Two-Step Equations Continued
Check
3. -3a + 10 = -20 -3a + 10 = -20
- 10 -10 -3(10) + 10 = -20
3a 30

-30 + 10 = -20
3
3
a = 10
-20 = -20
4. 5x – 22 = 78
+ 22 +22
5 x 100

5
5
x = 20
Check
5x – 22 = 78
5(20) – 22 = 78
100 – 22 = 78
78
= 78
Solving Equations By Combining Like Terms
Method:
1. Simplify the left side of the equal sign (if possible).
2. Simplify the right side of the equal sign (if possible).
Please Note: When simplifying, this could involve combining like
terms, distributive property, etc.
a) Distributive Property of Multiplication over Addition:
a(b + c) = ab + ac
b) Distributive Property of Multiplication over Subtraction:
a(b – c) = ab – ac
3. Gather all variables to one side of the equal sign by using
inverse operations.
4. Gather all constants to the opposite side of the variables by using inverse operations.
5. Isolate (get by itself) the variable by using inverse operations.
6. Check
*substitute solution into original equation
*perform steps for order of operations
34
Solving Equations By Combining Like Terms Continued
Examples
1. b + 10 -3 = 44  2
b+7
= 22
-7
-7
b
= 15
2. 4x + 8x – 2x + 7 = -13
10x + 7 = -13
- 7 = -7
10 x 20

10
10
x = -2
3. 33 = 4n – 7 + 6n
33 = 10n – 7
+7
+7
40 10n

10 10
4= n
Check
b + 10 – 3 = 44  2
(15) + 10 -3 = 44  2
22
= 22
Check
4x + 8x – 2x + 7 = -13
4(-2) + 8(-2) – 2(-2) + 7 = -13
-8 + -16 - -4
+ 7 = -13
-13
= -13
Check
33 = 4n – 7 + 6n
33 = 4(4) – 7 + 6(4)
33 = 16 - 7 + 24
33 = 33
35
Translating Algebraic Expressions and Equations
+
-
Add
Difference
Sum
Minus
Plus
Remainder
Total
less than
increased by decreased by
x
:
=
multiply
product
times
double
triple
divide
quotient
remainder
equals
is equal to
Is
1. Six more than a number b
1. 6 + b
2. Eight decreased by a number m
2. 8 - m
3. The product of four and a number x
3. 4x
4. The quotient when a number z is divided by fourteen
4. z  14
5. The value in cents of k dimes
5. 10k
6. Twice a number p increased by ten
6. 2p +10
7. Twelve more than a number x is seventeen
7. 12 + x = 17
8. Thirty-two less than a number m is eighteen
8. m – 32 = 18
9. Mark has q quarters worth a total of $12.50
9. 25q = 1250
9. .25q = 12.50
(decimal form)
10. Mary has d dimes and p pennies worth a total of $12.50
10. .10d + .01p = 12.50
(decimal form)
36
10. 10d + 1p = 1250
Distributive Property
Method:
1. Simplify the left side of the equal sign (if possible).
2. Simplify the right side of the equal sign (if possible).
Please Note: When simplifying, this could involve combining like
terms, distributive property, etc.
a) Distributive Property of Multiplication over Addition:
a(b + c) = ab + ac
b) Distributive Property of Multiplication over Subtraction:
a(b – c) = ab – ac
3. Gather all variables to one side of the equal sign by using
inverse operations.
4. Gather all constants to the opposite side of the variables by using inverse operations.
5. Isolate (get by itself) the variable by using inverse operations.
6. Check
*substitute solution into original equation
*perform steps for order of operations
Examples
Check
1. -4(y + 8) = 16
-4y – 32 = 16
+ 32 +32
4 y 48

4 4
y = -12
-4(y + 8) = 16
-4(-12 + 8) = 16
-4(-4)
= 16
16
= 16
105
 3(4  2b)
2.
5
21 = 12 – 6b
-12 -12
9 6b

6 6
Check
105
 3(4  2b)
5
21 = 3(4 – 2(-1.5))
21 = 3(4 + 3)
21 = 3(7)
21 = 21
-1.5 = b
37
Distributive Property Continued
3. -2(x – 3) = -3(-8)
-2x + 6 = 24
2 x 18

2 2
x = -9
Check
-2(x – 3) = -3(-8)
-2(-9 – 3) = -3(-8)
-2(-12)
24
=
4. 9 – 4(x -3) = 17
9 – 4x +12 = 17
24
= 24
21 – 4x
-21
= 17
= -21
4 x 4

4 4
x= 1
5. Three times the sum of x and 8 is 30. Find the number x.
Let x = the number
The number = x
=2
3(x + 8) = 30
3x + 24 = 30
-24 -24
3x 6

3 3
x=2
6. Five time the difference of x and 10 is 40.
Let x = the number
The number = x
= 18
5(x - 10) = 40
5x - 50 = 40
+50 +50
5 x 90

5
5
x = 18
38
Check
9 – 4(x – 3) = 17
9 – 4(1 – 3) = 17
9 – 4(-2)
= 17
9+ 8
= 17
17
= 17
Solving Equations With Variables On Both Sides
Method:
1. Simplify the left side of the equal sign (if possible).
2. Simplify the right side of the equal sign (if possible).
Please Note: When simplifying, this could involve combining like
terms, distributive property, etc.
a) Distributive Property of Multiplication over Addition:
a(b + c) = ab + ac
b) Distributive Property of Multiplication over Subtraction:
a(b – c) = ab – ac
3. Gather all variables to one side of the equal sign by using
inverse operations.
4. Gather all constants to the opposite side of the variables by using inverse operations.
5. Isolate (get by itself) the variable by using inverse operations.
6. Check
*substitute solution into original equation
*perform steps for order of operations
Examples
Check
1. 7m = 2m + 10 7m = 2m + 10
-2m -2m
7(2) = 2(2) + 10
5m 10

14 = 4 + 10
5
5
m= 2
14 =
14
2. y – 5 = 2y +10
-y
-y
Check
y – 5 = 2y + 10
(-15) – 5 = 2(-15) + 10
-5 = y + 10
-20
= -30 + 10
-10
-15 =
-20
=
- 10
y
39
-20
Solving Equations With Variables On Both Sides Continued
3. 3x = x + 2
-x -x
2x 2

2 2
x= 1
Check
3x = x + 2
3(1) = (1) + 2
3
5. 10y – (5y + 8) = 42
10y – 5y – 8 = 42
5y – 8 = 42
+8 = +8
5 y 50

5
5
y = 10
6. 3(a – 5) = 2(2a + 1)
3a – 15 = 4a + 2
-3a
-3a
-15 = a + 2
-2
-2
-17 = a
=
3
4. 5b – 2 = b + 10
-b
-b
4b – 2 =
+2
Check
5b – 2 = b + 10
5(3) – 2 = (3) + 10
10
15 - 2 =
+2
4b 12

4
4
b =3
Check
10y – (5y + 8) = 42
10(10) – (5  10 + 8) = 42
100 – 58 = 42
42 = 42
Check
3(a – 5) = 2(2a + 1)
3(-17 – 5) = 2(2  -17 + 1)
3(-22) = 2(-33)
-66 = -66
40
13
=
13
13
Solving Equations With Fractions
Method:
1. Determine the Lowest Common Denominator (L.C.D)
*Lowest Common Denominator (L.C.D) = Lowest Common Multiple (L.C.M)
2. Multiply each part of the equation by the L.C.D/L.C.M.
*This eliminates the denominators
CAUTION: If the L.C.D/L.C.M is being multiplied by a binomial, trinomial, etc.
write parenthesis around the polynomial first
3. Follow normal algebraic procedures
Examples
1.
2x  7 2x  9

3
6
10
 2x  7 
 2x  9 
30
  30
  303
 6 
 10 
L.C.D/L.C.M (6, 10, 1) = 30
10x + 35 – 6x + 27 = 90
4x + 62 = 90
-62 -62
4 x 28

4
4
x=7
Check
2x  7 2x  9

3
6
10
27 7 279

3
6
10
21 5

3
6 10
105 15

3
30 30
3=3
41
Solving Equations With Fractions Continued
2.
2 1 11 1
 

3x 3 6 x 4
L.C.D/L.C.M (3x, 3, 6x, 4) = 12x
 2
1
 11 
1
12 x   12 x   12 x   12 x 
 3x 
 3
 6x 
4
8 + 4x = 22 – 3x
+3x
+3x
8 + 7x = 22
-8
-8
7 x 14

7
7
x=2
Check
2 1 11 1
 

3x 3 6 x 4
2
1
11 1
 

3 2 3 6 2 4
2 1 11 1
  
6 3 12 4
4 4 11 3

 
12 12 12 12
8
8

12 12
2 2

3 3
42
Algebraic Equations and Solutions and Tape Diagrams
1.) Randy and Elisa went to a football game. Each person purchased a ticket and a $4
water. If the total cost of the tickets and water was $48, find the price of each ticket.
Algebraic Equations and Solution
Let t = each ticket price
Bottle water: $4
2(t + 4) = 48
2t + 8 = 48
-8 -8
𝟐𝒕
𝟐
=
𝟒𝟎
𝟐
t = 20
Each ticket is $20
Tape Diagram
t+4
t+4
48 – 8 = 40
2t = 40
t = 20
43
Algebraic Equations and Solutions and Tape Diagrams
2.) Tara needed to rent a big screen television for a family reunion. The initial cost was
$50 and 10 for each hour she rented the big screen television. If Tara spent a total of
$200, how many hours did she use the television?
Algebraic Equation and Solution
Let h = hours used big screen television
Initial cost = $50
10h + 50 = 200
-50
-50
𝟏𝟎𝒉
𝟏𝟎
=
𝟏𝟓𝟎
𝟏𝟎
h = 15 hours
Total hours = 15 + 1 = 16
Tape Diagram
10
10
10
10
10
10
10
10
10
200 – 50 = 150
150 ÷ 10 = 15
15 + 1 = 16 hours total
44
10
10
10
10
10
10
50
Discount Prices and Sales Tax
1.) An item that costs $120 is discounted 20%. Then an 8% tax is applied to the sale
price. Find the sale price including the tax.
Sale price (without tax) = 120(1 - .20)
= 120 (.8)
= 96
Sale price (with tax) = 96(1 + .08)
= 96(1.08)
= 103.68
2.) An item that costs $120 has an 8% tax applied to the cost. Then a 20% discount is
applied to the price with tax. Find the sale price including tax.
Price of item (including tax) = 120(1 + .08)
= 120(1.08)
= 129.60
Sale price (with discount applied) = 129.60(1 - .2)
= 129.60(.8)
= 103.68
PLEASE NOTE THAT WHETHER THE DISCOUNT IS APPLIED FIRST OR THE
TAX IS APPLIED FIRST, THE SALE PRICE WILL BE THE SAME.
45
Investment Terminology
L. Deposit: Deposits are added to an account balance, money is deposited into the account.
M. Gains: Gains are added to an account balance, as they are positive returns on the
investment.
N. Withdrawals: Withdrawals are subtracted from an account balance; money is taken out
of the account.
O. Losses: Losses are subtracted from an account balance; as they are negative returns on the
investment.
P. Fees: Fees are subtracted from an account balance; as the bank/financial company is
charging you for a service.
46