Download Prof. Darrick Chang - Lecures - ICFO Schools on the Frontiers of Light

Darrick Chang
ICFO – The Institute of Photonic Sciences
Barcelona, Spain
School on Quantum Nano- and Opto-Mechanics
July 8, 2016
Motivation
• Optomechanics: unprecedented levels of control over
interactions between motion and light
Ground-state cooling
Chan et al, Nature 478, 89 (2011)
Generation of squeezed light
Safavi-Naeini et al, Nature
500, 185 (2013)
Entanglement of light and
motion
Palomaki et al, Science 342, 710
(2013)
• Future: exploring the boundaries of quantum physics with
optomechanical systems?
Ultracold atoms
???
Optomechanical arrays
Walter and Marquardt,
arXiv:1510.06754v1 (2015)
High-Tc superconductors
Motivation
• The difficulties with conventional systems:
• Large motional mass
• Weak optomechanical interactions (linearized equations)
• Short lifetimes/coherence times of phonons and photons
Levitated optomechanics
Motivation
• What about atoms?
• Rich history of optical cooling/trapping (no back-action)
• Pristine control over long-lived internal (“spin”) states and
their interactions with photons
Ion traps
Atomic ensembles
Cavity QED
• Question:
Can we actively manipulate atomic quantum motion, and
interact strongly with atomic spins and photons?
Goals of lectures
• Introduction to quantum atom-light interactions
• Jaynes-Cummings model (cavity QED)
• How to implement “conventional” optomechanics with atoms
• Creating progressively richer behavior with atoms?
• Self-organization
Nanofibers
Photonic crystals
• Tailoring optomechanical interactions with new platforms
• Quantum many-body physics with atomic spin and motion
Introduction to atom-light interactions
The Hamiltonian
• A “believable” proof
• When you shine light (optical frequencies) on an atom, the
response is essentially electric
• Field induces a dipole moment, so…
𝐻 = −𝑑 ⋅ 𝐸(𝑟atom )
• How do we quantize the dipole moment and the field?
Quantization of dipole operator
• 𝑑 = −𝑒𝑟elec
• Consider a hydrogen-like atom
• Eigenstates of the Coulomb potential
1
Transition energy from n to n+1: ∝ 𝑛2
Energy
“2p”
𝑛 = 2, 𝑙 = 𝑝
|𝒆〉
“1s”
𝑛 = 1, 𝑙 = 𝑠
|𝒈〉
• Take matrix elements of 𝑑 with eigenstates
𝑑 = −𝑒
𝑗 〈𝑗|𝑟elec 𝑗′ 〈𝑗′|
𝑗,𝑗 ′ =𝑒,𝑔
Quantization of dipole operator
“2p”
𝑛 = 2, 𝑙 = 𝑝
|𝒆〉
“1s”
𝑛 = 1, 𝑙 = 𝑠
|𝒈〉
𝑑 = −𝑒
𝑗 〈𝑗|𝑟elec 𝑗′ 〈𝑗′|
𝑗,𝑗 ′ =𝑒,𝑔
• Consider symmetries
𝑔 𝑟elec 𝑔 = ∫ 𝑑𝑟 even fn. × odd × even = 0
𝑒 𝑟elec 𝑒 = 0
• Final form:
𝑑 = −𝑑0 (|e〉〈𝑔| + |g〉〈𝑒|)
Contains details of atomic wavefunction, can relate to more observable quantities
• Induces transitions between ground and excited states
Quantization of dipole operator
“2p”
𝑛 = 2, 𝑙 = 𝑝
|𝒆〉
“1s”
𝑛 = 1, 𝑙 = 𝑠
|𝒈〉
𝑑 = −𝑒
𝑗 〈𝑗|𝑟elec 𝑗′ 〈𝑗′|
𝑗,𝑗 ′ =𝑒,𝑔
• Consider symmetries
𝑔 𝑟elec 𝑔 = ∫ 𝑑𝑟 even fn. × odd × even = 0
𝑒 𝑟elec 𝑒 = 0
• Easier notation:
𝑑 = −𝑑0 (𝜎𝑒𝑔 + 𝜎𝑔𝑒 )
Definition: 𝜎𝑖𝑗 = 𝑖 〈𝑗|
Field quantization
• Now quantize field operator 𝐸(𝑟)
• Let’s draw an analogy: a (unitless) harmonic oscillator mass
Hamiltonian
Dynamics
(Heisenberg
picture)
Ladder
operator
representation
𝐻 = (𝑥 2 + 𝑝2 )/2
𝑑𝑥/𝑑𝑡 = 𝑝
𝑑𝑝/𝑑𝑡 = −𝑥
𝑥=
𝑝=
1
2
𝑖
2
𝑎
+𝑎
(𝑎
− 𝑎)
• Physical interpretation:
𝐻=𝑎 𝑎
Number of quantized excitations (phonons)
Field quantization
• Now quantize field operator 𝐸(𝑟)
• Compare to free-space electromagnetic field (single mode 𝜔)
Hamiltonian
Dynamics
(Heisenberg
picture)
Ladder
operator
representation
𝐻 = (𝑥 2 + 𝑝2 )/2
𝑑𝑥/𝑑𝑡 = 𝑝
𝑑𝑝/𝑑𝑡 = −𝑥
𝑥=
𝑝=
1
2
𝑖
2
𝑎
+𝑎
(𝑎
− 𝑎)
𝐻 ∼ ∫ 𝑑𝑟(𝐸 2 + 𝐵2 )/2
𝑑𝐸/𝑑𝑡 = c 2 𝛻 × 𝐵
𝑑𝐵/𝑑𝑡 = −𝛻 × 𝐸
𝐸(𝑧) = 𝐸0 𝜖𝑘 (𝑎𝑘 𝑒 𝑖𝑘𝑧 + 𝑎𝑘 𝑒 −𝑖𝑘𝑧 )
Normalization – deal with this later…
• Physical interpretation:
• 𝑎𝑘 creates a photon of wavevector k, and energy 𝜔 = 𝑐𝑘
• Spatial profile of photon is given by 𝑒 𝑖𝑘𝑧
Field normalization
𝐸(𝑧) = 𝐸0 𝜖𝑘 (𝑎𝑘 𝑒 𝑖𝑘𝑧 + 𝑎𝑘 𝑒 −𝑖𝑘𝑧 )
• What is the normalization 𝐸0 ?
• i.e., what is the characteristic “electric field” of a single
photon?
• Semi-classical argument: energy of photon in a box V
• Field strength: 𝐸0 ∼
ℏ𝜔
𝜖0 𝑉
• Physically: energy of single photon is fixed, but its intensity
grows if you pack it in a small box
To summarize:
• Interaction Hamiltonian
𝐻int = −𝑑 ⋅ 𝐸(𝑟atom )
• Interaction g is small compared to bare frequencies of photon
and atomic transition
• The energy “non-conserving” terms have negligible impact
𝐻int ≈ 𝑔(𝜎𝑒𝑔 𝑎𝑓 𝑟 + 𝜎𝑔𝑒 𝑎 𝑓 ∗ 𝑟 )
𝐻0 = 𝜔𝑒𝑔 𝜎𝑒𝑒 + 𝜔𝑎 𝑎
Jaynes-Cummings model
Cavity QED
• Jaynes-Cummings model: interaction of atom with single mode
of a cavity
𝐻 = 𝑔(𝑟) 𝜎𝑒𝑔 𝑎 + 𝜎𝑔𝑒 𝑎† + Δ𝑎† 𝑎
|𝑒, 𝑛〉
𝑔 𝑛+1
Δ = 𝜔cavity − 𝜔atom
(defining energy relative to
atomic transition)
|𝑔, 𝑛 + 1〉
• So far, ideal (no losses)
• Conserves total number of excitations (atomic+photonic)
• Can solve each number manifold separately
Cavity QED
𝐻 = 𝑔(𝑟) 𝜎𝑒𝑔 𝑎 + 𝜎𝑔𝑒 𝑎† + Δ𝑎† 𝑎
|𝑒, 𝑛〉
Δ = 𝜔cavity − 𝜔atom
𝑔 𝑛+1
|𝑔, 𝑛 + 1〉
• Example
• When n=0, reversible “vacuum Rabi oscillations” between
photon and excited atom
Cavity QED
𝐻 = 𝑔(𝑟) 𝜎𝑒𝑔 𝑎 + 𝜎𝑔𝑒 𝑎† + Δ𝑎† 𝑎
Δ = 𝜔cavity − 𝜔atom
|𝑒, 𝑛〉
𝑔 𝑛+1
|𝑔, 𝑛 + 1〉
• More generally, can diagonalize each number manifold
• Limit where Δ ≫ 𝑔 𝑛
• Eigenstates are almost purely
photonic or atomic
Eliminating degrees of freedom
• A priori, we have a complicated system with many degrees of
freedom (motion, spin, photon)!
• In the far-detuned regime, we can get rid of one of them (spin
or photon) in perturbation theory
• Photon branch (eliminating spin)
• Interpretation: refractive index of atom shifts resonance
frequency of cavity
Conventional optomechanics with atoms
Effective Hamiltonian
• Simplified effective Hamiltonian in the photon branch:
𝐻=
𝑖∈atoms
𝑝𝑖2
𝑔2 (𝑥𝑖 ) †
+ 𝜔cav +
𝑎 𝑎
2𝑚
Δ
• Recovering “normal” optomechanics:
• Take a Fabry-Perot cavity 𝑔 𝑥 = 𝑔0 cos 𝑘𝑥
• Add a tight (harmonic) external trapping potential for atoms
• Can linearize in the displacement if the trap confines atoms to
distances 𝑥𝑖 ≪ 𝜆
𝐻𝑂𝑀 =
𝑖∈atoms
𝑔2 (𝑥𝑖 ) †
𝑎 𝑎≈
Δ
𝑖∈atoms
2𝑔 𝑥𝑒𝑞 𝑔′ 𝑥𝑒𝑞
𝑥𝑖 𝑎† 𝑎 ≡ 𝐺𝑥𝐶𝑀 𝑎† 𝑎
Δ
Effective Hamiltonian
• Standard optomechanical interaction with atomic CM mode
2
𝑝𝐶𝑀
1
2
𝐻=
+ 𝑀𝜔2𝑇 𝑥𝐶𝑀
+ 𝐺𝑥𝐶𝑀 𝑎 † 𝑎
2𝑀 2
• “Typical” numbers
Experimental setup (StamperKurn, UC Berkeley)
PRL 105, 133602 (2010)
Nature Phys. 12, 27 (2016)
(+ decoupled relative degrees of freedom)
Atom number 𝑁𝑎𝑡𝑜𝑚 ∼ 103
Total mass 𝑀 ∼ 10−22 kg
Trap frequency 𝜔 𝑇 ∼ 2𝜋 × 100 kHz
Cavity linewidth 𝜅 ∼ 2𝜋 × 1 MHz
Optomechanical coupling 𝐺𝑥𝑧𝑝 ∼ 2𝜋 × 1 MHz
• Not sideband resolved
• Can use other atomic physics tricks
to reach motional ground state
New physics?
• We worked rather hard to get to the conventional regime!
• Added an external potential
• Tightly trap atoms to linearize the displacement
• Numbers are not especially unique
• Can we find physics more unique to atoms?
Jaynes-Cummings model:
Spin branch
Eliminating the photons
• A priori, we have a complicated system with many degrees of
freedom (motion, spin, photon)!
• What if we eliminate the photons instead?
Being more careful…
• Let’s do the calculation more carefully, to relate to some wellknown concepts from cavity QED
• Goal: start from full system dynamics (including losses) and
eliminate the photon
Free-space
emission Γ′
Cavity decay
|𝑒, 𝑛〉
𝜅
𝑔 𝑛+1
|𝑔, 𝑛 + 1〉
𝐻 = 𝑔 𝑟 𝜎𝑒𝑔 𝑎 + 𝜎𝑔𝑒 𝑎†
′
𝑖Γ
𝑖𝜅 †
† −
𝜎𝑒𝑒 − 𝑎 𝑎
+ Δ𝑎 𝑎
2
2
• Rigorously, should go to density matrix formalism or add
“quantum jumps,” but not necessary here
Perturbation theory
• Consider the effect of cavity coupling on state |𝑒, 0〉 in secondorder perturbation theory
𝛿𝜔𝑒 =
𝑚
𝛿𝜔𝑒 =
𝑒, 0 𝐻int 𝑚 〈𝑚|𝐻int |𝑒, 0〉
0 − 𝜔𝑚
𝑒, 0 𝐻int 𝑔, 1 〈𝑔, 1|𝐻int |𝑒, 0〉
−(Δ − 𝑖𝜅 2)
𝑔2 𝑟
𝑔2 𝑟 Δ
𝛿𝜔𝑒 = −
=− 2
Δ − 𝑖𝜅 2
Δ + 𝜅 2
𝜅
𝑔2 𝑟
2 − 𝑖 2 Δ2 + 𝜅 2
2
Cavity-induced decay and shifts
• Cavity-enhanced decay rate
• On resonance:
𝑔2 𝜅
Γtotal = Γ′ + 2
Δ + 𝜅/2
4𝑔2
Γtotal = Γ′ +
𝜅
• “Cooperativity” factor 𝐶 =
• Far off resonance:
Γtotal
𝑔2
𝜅Γ′
2
gives the branching ratio
𝑔2
≈ Γ′ + 𝜅 2
Δ
• Cavity-induced shift of excited state
Δ𝑔2
𝛿𝜔𝑒 = − 2
Δ + 𝜅/2
2
• Far off resonance: 𝛿𝜔𝑒 = −𝑔2 /Δ agrees with previous
eigenvalue calculation
Two atoms in cavity
• Goal: coherent excitation exchange between two atoms
Γ′
|𝑒2 , 0〉
|𝑒1 , 0〉
𝑔
𝑔
𝜅
|𝑔1 𝑔2 , 1〉
• Apply similar perturbation theory on atomic excited state
manifold
• Find an equivalent Hamiltonian to describe the coherent
dynamics (energy shifts and exchange rate)
𝐻eff =
𝑖,𝑗=1,2
𝑔 𝑟𝑖 𝑔 𝑟𝑗 (𝑖) (𝑗)
−
𝜎𝑒𝑔 𝜎𝑔𝑒
Δ
Two atoms in cavity
• Equivalent non-Hermitian Hamiltonian to describe dissipation
𝐻d = −𝑖
𝑖,𝑗=1,2
Γ′ 𝑖
𝜎𝑒𝑒 −
2
𝑖,𝑗=1,2
𝑔 𝑟𝑖 𝑔 𝑟𝑗 𝜅 (𝑖) (𝑗)
2𝑖
𝜎𝑒𝑔 𝜎𝑔𝑒
2
Δ
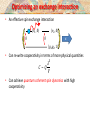
Optimizing an exchange interaction
• An effective spin exchange interaction
|𝑒2 , 0〉
|𝑒1 , 0〉
𝑔
𝑔
• Effective Hamiltonian:
𝐻eff
𝜅
|𝑔1 𝑔2 , 1〉
𝑔2 1 2
≈ − 𝜎𝑒𝑔 𝜎𝑔𝑒 + ℎ. 𝑐.
Δ
• Transfer of excitation from one atom to another in time 𝑇 ∼
Δ/𝑔2
• Total error (loss) during that time: 𝑇 Γ′ + 𝑔2 𝜅/Δ2
• Optimizing with respect to Δ:
𝑑 Error
1
= 0 → Error ∼
∼
𝑑Δ
𝐶
𝜅Γ′
𝑔2
Optimizing an exchange interaction
• An effective spin exchange interaction
|𝑒2 , 0〉
|𝑒1 , 0〉
𝑔
𝑔
𝜅
|𝑔1 𝑔2 , 1〉
• Can re-write cooperativity in terms of more physical quantities
𝜆3
𝐶∼𝑄
𝑉
• Can achieve quantum coherent spin dynamics with high
cooperativity
Spin-motion coupling
• Focus in cavity QED is usually on spin dynamics, or spin-photon
coupling
• Effective Hamiltonian
𝐻eff =
𝑖,𝑗=1,2
𝑔 𝑟𝑖 𝑔 𝑟𝑗 (𝑖) (𝑗)
−
𝜎𝑒𝑔 𝜎𝑔𝑒
Δ
• (Mechanical potential) x (Spin term) → spin-dependent force
• What are the physical consequences and possibilities?
Self-organization of atoms in a cavity
Setup of self-organization
• Schematic of idea:
Atoms excite and emit photons into
cavity
Pump Ω, 𝛿𝐿
Setup of self-organization
• Schematic of idea:
Buildup of standing wave
intensity provides a force
Pump Ω, 𝛿𝐿
Atomic position dictates
coupling strength to
cavity field 𝑔(𝑥)
Back-action!
Cavity intensity builds
up and provides force
on atoms
• A priori, many degrees of freedom coupled together
• Possibility for elegant “emergent” phenomena?
• “Self-organization”
Setup of self-organization
• Schematic of idea:
Buildup of standing wave
intensity provides a force
Pump Ω, 𝛿𝐿
• Effective Hamiltonian of system
𝐻eff =
𝑖
𝑝𝑖2
−
2𝑚
𝑔02 cos 𝑘𝑥𝑖 cos 𝑘𝑥𝑗 𝑖 𝑗
𝜎𝑒𝑔 𝜎𝑔𝑒 +
Δ
𝑖,𝑗
cavity-mediated spin interaction
−𝑖
𝑖
Γ′ 𝑖
𝜎𝑒𝑒 −
2
𝑖,𝑗
(𝑖)
𝑖
external pump
𝑔 𝑟𝑖 𝑔 𝑟𝑗 𝜅 (𝑖) (𝑗)
−2𝑖
𝜎𝑒𝑔 𝜎𝑔𝑒
2
Δ
dissipation
(𝑗)
Ω 𝜎𝑒𝑔 + 𝜎𝑔𝑒
(𝑖)
− 𝛿𝐿 𝜎𝑒𝑒
Equations of motion
• Let’s consider the Heisenberg equations of motion:
𝑑𝑥𝑖 𝑝𝑖
=
𝑑𝑡
𝑚
𝑑𝑝𝑖
𝜕𝐻
𝑔02 𝑘
=−
=−
𝑑𝑡
𝜕𝑥𝑖
Δ
(𝑖) (𝑗)
sin 𝑘𝑥𝑖 cos 𝑘𝑥𝑗 𝜎𝑒𝑔 𝜎𝑔𝑒
𝑗
• In principle, quantum correlations could make the system very
rich and challenging!
• Would be interesting if correlations matter (seminar!)
• Some reasons to think that correlations break down:
• Motion should be initially cold (ground state, quantum
degenerate)
• Motional time scales are very slow (atoms scatter many photons)
• Scattering leads to recoil heating and breaks spin correlations
Equations of motion
• Thus, we’ll assume that we can de-correlate all variables
• Solve classical equations of motion
• For simplicity, drop
symbols, with understanding that
all operators are just expectation values now
• In general, the forces are not derivable from a potential
• Equations of motion for spins
Weak scattering limit
• Solutions can be studied numerically, but the “weak scattering”
limit is particularly simple
• Each atom then has a constant, identical dipole moment
𝜎𝑔𝑒 ≈
𝑖Ω
𝑖𝛿𝐿 −Γ′ /2
(ignoring atomic saturation)
• Going back to forces:
• Special case, derivable from a mechanical potential!
Self-organization
• Consider positive detuning Δ > 0
• Energy would be lowest if cos 𝑘𝑥𝑖 cos 𝑘𝑥𝑗 = 1 for all pairs
• Atoms either all sit on “even” anti-nodes 𝑘𝑥𝑖 = 2𝜋𝑛 or “odd”
anti-nodes 𝑘𝑥𝑖 = 2𝜋(𝑛 + 1 2)
“Even”
“Odd”
• Atoms can self-organize starting from a random distribution,
and spontaneously break the symmetry
Physical origin of symmetry breaking
• Consider just two atoms
Positioned at
different signs
Pump Ω
• The pump field drives both atoms equally, creating dipoles
oscillating with same phase
• Dipoles with same phase, but sitting in an even and odd antinode, drive a cavity field with opposite phases
• No cavity field due to interference!
Summary of self-organization
 Phenomena related to back-action, going beyond conventional
optomechanics
 Nonlinear in the displacement of atomic positions
 Emergence of phase transitions
Baumann et al, Nature 464,
1301 (2010)
Classical behavior (at least in the limits of our solution)
Spin nature is not important
Maybe not surprising? Cavity mode already has standing wave
structure, so “of course” atoms should organize in that pattern
Beyond cavity QED
• Have seen the features and limitations of atom-optomechanics
with cavity QED
• New possibilities with other platforms for atom-light coupling?
Atom-nanofiber interfaces
Atoms coupled to photonic
crystal waveguides
• Need to find a more general model for atom-light interactions,
beyond Jaynes-Cummings
• This new “spin model” almost automatically points us to
photonic crystals as the route toward quantum behavior
Quantum spin model for atom-light interfaces
From Jaynes-Cummings to Green’s functions
|𝑒2 , 0〉
|𝑒1 , 0〉
𝑔
𝑔
𝜅
|𝑔1 𝑔2 , 1〉
• Working in the limit when photons are negligible (spin branch):
𝐻eff
𝑔2
≈−
Δ
𝑗
𝑖
cos 𝑘𝑥𝑖 cos 𝑘𝑥𝑗 𝜎𝑒𝑔
𝜎𝑔𝑒
𝑖,𝑗
• The spatial function looks like a Green’s function
Green’s function
• Physical interpretation
• G describes the electric field at point r, due to a (normalized)
oscillating dipole at r’
• It is a tensor quantity (𝛼, 𝛽 = 𝑥, 𝑦, 𝑧) because the source dipole can
have three orientations, and the electric field at r is a vector
• Can ignore tensor nature for our purposes
• Simple case: free space
Green’s function form of spin model
• Claim: coherent evolution given by
𝑗
2
𝐻eff = −𝜇0 𝑑02 𝜔𝑒𝑔
𝑖
Re 𝐺(𝑟𝑗 , 𝑟𝑖 , 𝜔𝑒𝑔 ) 𝜎𝑒𝑔
𝜎𝑔𝑒
𝑖,𝑗
• Losses:
𝑗
2
𝜌 = 𝐿 𝜌 = −𝜇0 𝑑02 𝜔𝑒𝑔
𝑗
𝑗
𝑖
𝑖
𝑖
Im 𝐺(𝑟𝑗 , 𝑟𝑖 , 𝜔𝑒𝑔 ) 𝜎𝑒𝑔
𝜎𝑔𝑒 𝜌 + 𝜌𝜎𝑒𝑔
𝜎𝑔𝑒 − 2𝜎𝑔𝑒 𝜌𝜎𝑒𝑔
𝑖,𝑗
• In short (non-Hermitian Hamiltonian):
𝑗
2
𝐻eff = −𝜇0 𝑑02 𝜔𝑒𝑔
𝑖 𝜎
𝐺(𝑟𝑗 , 𝑟𝑖 , 𝜔𝑒𝑔 )𝜎𝑒𝑔
𝑔𝑒
𝑖,𝑗
A “trivial” example
• Must work for a single atom in free-space too
𝑗
2
𝐻eff = −𝜇0 𝑑02 𝜔𝑒𝑔
𝑖
𝐺(𝑟𝑗 , 𝑟𝑖 , 𝜔𝑒𝑔 )𝜎𝑒𝑔
𝜎𝑔𝑒
𝑖,𝑗
2
𝐻eff = −𝜇0 𝑑02 𝜔𝑒𝑔
𝐺(𝑟𝑎𝑡𝑜𝑚 , 𝑟𝑎𝑡𝑜𝑚 , 𝜔𝑒𝑔 )𝜎𝑒𝑔 𝜎𝑔𝑒
𝐻eff =
2
−𝜇0 𝑑02 𝜔𝑒𝑔
𝑖𝜔𝑒𝑔
𝑖ℏΓ0
𝜎𝑒𝑒 ≡ −
𝜎𝑒𝑒
6𝜋𝑐
2
3
𝜇0 𝑑02 𝜔𝑒𝑔
Γ0 =
3𝜋ℏ𝑐
• Recover spontaneous emission rate of atom, usually derived by
Fermi’s Golden Rule!
Justification of Hamiltonian
𝑗
2
𝐻eff = −𝜇0 𝑑02 𝜔𝑒𝑔
𝑖
𝐺(𝑟𝑗 , 𝑟𝑖 , 𝜔𝑒𝑔 )𝜎𝑒𝑔
𝜎𝑔𝑒
𝑖,𝑗
• Atoms produce non-classical states of light, but quantum and
classical light propagate in the same way
• Can use classical E&M Green’s function
• Re and Im parts dictate coherent evolution and dissipation
• Classically: field in/out of phase with oscillating dipole
stores time-averaged energy or does time-averaged work
• Limits of validity
• No strong coupling effects (e.g. vacuum Rabi oscillations)
• Ignores time retardation
|𝑒〉
Γ
~10 meters
Photon
|𝑔〉
A universal model
𝑗
2
𝐻eff = −𝜇0 𝑑02 𝜔𝑒𝑔
𝑖
𝐺(𝑟𝑗 , 𝑟𝑖 , 𝜔𝑒𝑔 )𝜎𝑒𝑔
𝜎𝑔𝑒
𝑖,𝑗
• This Hamiltonian equally captures any system of atoms
interacting with light
• Cavity QED
• Free-space atomic ensembles
• Nanophotonic systems
• Enables one to compare very different systems on an equal
footing
Basics of atom-nanofiber experiment
Modes of nanofiber
• Optical fiber: guides light by total internal reflection
𝑛𝑐𝑜𝑟𝑒 > 1
𝑛𝑐𝑙𝑎𝑑𝑑𝑖𝑛𝑔 = 1
• Method of solution: use separation of variables for fields in
core and cladding, and apply E&M boundary conditions
• Highlights of solution:
• Field actually evanescently leaks into cladding (vacuum) region
• The evanescent tail becomes very long for thin fibers 𝑅fiber ≪ 𝜆
• Solution respects diffraction limit
Optical trapping of atoms
• Guided mode intensity profile
250 nm radius fiber
n = 1.45 (SiO2)
937 nm (free-space) wavelength
• How to trap atoms:
|𝒆〉
|𝒆〉
|𝒈〉
|𝒈〉
𝝎𝑳 < 𝝎𝒆𝒈
𝝎𝑳 > 𝝎𝒆𝒈
𝜶 𝝎𝑳 > 𝟎
𝜶 𝝎𝑳 < 𝟎
Optical tweezer potential
1
𝑈 𝑟 = − Re 𝛼 𝜔𝐿 𝐸 𝑟
2
2
• Atoms seek intensity maxima (minima) for red (blue) detuned
beams
Optical trapping of atoms
• Guided mode intensity profile
250 nm radius fiber
n = 1.45 (SiO2)
937 nm (free-space) wavelength
• Use a combination of red and blue detuned beams to create a
Trap potential
stable potential
•
•
Red-detuned (lower freq.) has a longer
wavelength, so it attracts atoms toward
fiber at large distances
Blue-detuned creates a short-range
repulsion, preventing atom from crashing
into fiber surface
• Typical trap depth: 100’s 𝜇K
• Lifetime (without cooling): 100 ms
Trap minima
Loading the trap
• Experimental setup:
MOT
• The red-detuned beam can be sent in from both sides to create
a standing wave (1D optical lattice for atoms)
• Many trapping minima, but need to fill them with atoms!
• A magneto-optical trap probabilistically cools a cloud of cold
atoms into the trap sites
• Typically ~50% filling probability
Atom-light interactions
• Transmission spectra reveal properties of atomic ensemble
Good fit to broadened
Lorentzian response
On resonance:
attenuation ~ exp
𝜆20
− 𝑁atom
𝐴
~ exp(−OD)
OD~0.08 for single atom
𝑁𝑎𝑡𝑜𝑚 ~103
Atom-nanofiber spin model
Spin model revisited
• Recall in general:
𝑗
2
𝐻eff = −𝜇0 𝑑02 𝜔𝑒𝑔
𝑖 𝜎
𝐺(𝑟𝑗 , 𝑟𝑖 , 𝜔𝑒𝑔 )𝜎𝑒𝑔
𝑔𝑒
𝑖,𝑗
• In principle, we can solve for G exactly (cylindrical fiber)
• Separation of variables, Bessel functions, …
A toy model
• Suppose we have a perfect, translationally invariant 1D system
• Physically, no diffraction, just propagation phase
• Green’s function
• Spin model Hamiltonian
𝐻eff
𝑖Γ1D
=−
2
𝑗
𝑖 𝜎
exp(𝑖𝑘 𝑧𝑖 − 𝑧𝑗 ) 𝜎𝑒𝑔
𝑔𝑒
𝑖,𝑗
• For single atom, spontaneous emission into fiber 𝐻eff
𝑖Γ1D
=−
𝜎𝑒𝑒
2
• Γ1D obtained from more exact calculations or fits to
experiment
A toy model
• So far, not very physically realistic
𝐻eff
𝑖Γ1D
=−
2
exp(𝑖𝑘 𝑧𝑖 −
𝑖,𝑗
𝑖 𝜎𝑗
𝑧𝑗 ) 𝜎𝑒𝑔
𝑔𝑒
𝑖Γ′
−
2
𝑖
𝜎𝑒𝑒
𝑖
• An atom emits 100% of the time into the guided mode
• Add phenomenological, independent emission rate Γ′ into free
space
• Γ ′ ∼ 10Γ1𝐷 for nanofiber experiments
Self-organization of fibers in waveguide
(recall the discussion session!)
Schematic of setup
•
•
•
•
Similar as in optical cavity
Initially random atoms (transversely trapped, but free axially)
Pump atoms from the side
Atoms scatter photons into the guided mode, which produces
forces on other atoms
𝑧𝑖
|𝑒〉
|𝑒〉
|𝑒〉
|𝑔〉
|𝑔〉
|𝑔〉
𝑧𝑖+1
• Stable self-organization configurations?
𝑧𝑖+2
Taking a closer look at the Hamiltonian
𝐻eff
𝑖Γ1D
=−
2
exp 𝑖𝑘 𝑧𝑖 − 𝑧𝑗
𝑖 𝜎𝑗
𝜎𝑒𝑔
𝑔𝑒
𝑖,𝑗
𝑖Γ′
−
2
𝑖
𝜎𝑒𝑒
𝑖
• Let’s break up effective Hamiltonian into Hermitian and
dissipative components
• Hermitian part:
𝐻eff
Γ1D
=
2
𝑗
𝑖 𝜎
sin 𝑘 𝑧𝑖 − 𝑧𝑗 𝜎𝑒𝑔
𝑔𝑒
𝑖,𝑗
• Dissipative (anti-Hermitian) part:
𝐻eff
iΓ1𝐷
=−
2
cos 𝑘 𝑧𝑖 − 𝑧𝑗
𝑖,𝑗
𝑖 𝜎𝑗
𝜎𝑒𝑔
𝑔𝑒
𝑖Γ′
−
2
𝑖
𝜎𝑒𝑒
𝑖
• Γ′ is large in realistic systems
• Even if Γ ′ = 0, coherent and dissipative strengths in waveguide
have characteristically equal strengths
• Later… how to fix this!
Outline of procedure to solve
• Full effective Hamiltonian
𝐻eff
=
𝑖
𝑝𝑖2
𝑖Γ ′ 𝑖
𝑖Γ1D
𝑖
𝑖
− 𝛿𝐿 +
𝜎𝑒𝑒 + Ω(𝜎𝑒𝑔 + 𝜎𝑔𝑒 ) −
2𝑚
2
2
exp 𝑖𝑘 𝑧𝑖 − 𝑧𝑗
𝑗
𝑖 𝜎
𝜎𝑒𝑔
𝑔𝑒
𝑖,𝑗
• Heisenberg equations of motion
• De-correlate all operators (classical expectation values)
• Ignore atomic saturation effects (𝜎𝑒𝑒 ≈ 0, 𝜎𝑔𝑔 ≈ 1)
(Γ ≡ Γ1𝐷 + Γ ′ )
A convenient parametrization
• Describe spacing between atoms in terms of an integer +
fractional number of wavelengths
• Spin model is periodic in distances (𝑒 𝑖𝑘|𝑧𝑖 −𝑧𝑗 | ), so integers 𝑛𝑖 do
not matter
Weak-scattering limit
𝛿𝐿 = 𝜔laser − 𝜔0
𝑁Γ1𝐷
−Γ 0 Γ
−𝑁Γ1𝐷
• External pump field is much larger than scattered field, atoms have
same induced dipole moment
• Minimization of mechanical potential energy
𝐻eff
Γ1𝐷
=
2
𝑗
𝑖
𝜎𝑒𝑔
𝜎𝑔𝑒
all pairs
sin 𝑘0 𝑧𝑖 − 𝑧𝑗
Γ1𝐷 𝜎𝑒𝑒
≈
2
sin 𝑘0 𝑧𝑖 − 𝑧𝑗
all pairs
2 atoms: 𝒅 =
𝟑𝝀
𝟒
Weak-scattering limit
𝛿𝐿 = 𝜔laser − 𝜔0
𝑁Γ1𝐷
−Γ 0 Γ
−𝑁Γ1𝐷
• External pump field is much larger than scattered field, atoms have
same induced dipole moment
• Minimization of mechanical potential energy
𝐻eff
Γ1𝐷
=
2
𝑗
𝑖
𝜎𝑒𝑔
𝜎𝑔𝑒
all pairs
sin 𝑘0 𝑧𝑖 − 𝑧𝑗
Γ1𝐷 𝜎𝑒𝑒
≈
2
sin 𝑘0 𝑧𝑖 − 𝑧𝑗
all pairs
N atoms: 𝒅 = 𝝀𝟎 (𝟏 −
𝟏
)
𝟐𝑵
General numerical procedure
• No analytical solution beyond weak scattering limit
• Difficult to directly solve steady state for 3N highly nonlinear
equations!
−𝛾𝑝 /2
• Approach
• Start at large laser detuning |𝛿|, use initial atomic positions
corresponding to weak scattering solution
• Add an artificial momentum damping
• Integrate differential equations in time until steady state {𝑧𝑖,𝑠𝑠 } is
reached
• Decrease |𝛿| by small amount, take the previous steady state
solution as the new initial condition
Red detuning
𝛿𝐿 = 𝜔laser − 𝜔0
−𝑁Γ1𝐷
−Γ 0 Γ
𝑁Γ1𝐷
• Atoms have an effective refractive index 𝑛eff > 1
• Expect a contraction of lattice constant
N atoms: 𝒅 ≈ 𝝀𝐞𝐟𝐟 (𝟏 −
𝟏
),
𝟐𝑵
𝝀𝐞𝐟𝐟 < 𝝀𝟎
Simulation vs. effective index model,
Γ
N=150 atoms, 1𝐷 = 0.25
Γ
Blue detuning
𝛿𝐿 = 𝜔laser − 𝜔0
−𝑁Γ1𝐷
−Γ 0 Γ
𝑁Γ1𝐷
• Naïvely: expansion of lattice constant
• But if 𝑑 ≈ 𝜆0 , it is known that the atoms become a good Bragg
reflector, and the “refractive index” argument is not consistent
• Actual: two “bound collective super-atoms”
• Minimize effective two- “super-atom” potential
Simulation
• Numerical simulation of N=150 atoms, random initial positions
Fractional positions 𝑓𝑗 versus time
Possible because
of infinite-range
interactions!
Signatures of self-organization
• Distinct transmission and reflection spectra of probe beams
• Photonic band structure and band gaps
Reflection versus pump and
probe detunings
Γ
N=150 atoms, 1𝐷 = 0.25
Γ
Summary of self-organization
 Phenomena related to back-action, going beyond conventional
optomechanics
 Nonlinear in the displacement of atomic positions
 Surprising: order emerges from a truly translationally invariant
system
Classical behavior
Spin nature is not important (spin-dependent forces)
Recall the problem
• Hermitian part of fiber Hamiltonian:
𝐻eff
Γ1D
=
2
𝑗
𝑖
sin 𝑘 𝑧𝑖 − 𝑧𝑗 𝜎𝑒𝑔
𝜎𝑔𝑒
𝑖,𝑗
• Dissipative (anti-Hermitian) part:
𝐻eff
iΓ1𝐷
=−
2
cos 𝑘 𝑧𝑖 − 𝑧𝑗
𝑖,𝑗
𝑖 𝜎𝑗
𝜎𝑒𝑔
𝑔𝑒
𝑖Γ′
−
2
𝑖
𝜎𝑒𝑒
𝑖
• Even if Γ ′ = 0, coherent and dissipative strengths in waveguide
have characteristically equal strengths
• Expect emission to break down correlations
• Dissipation comes from having a set of optical modes at the
atomic resonance frequency
• Need to get rid of this!
The fix – photonic crystals
Photonic crystal waveguides
• Normal fiber: light guided by total internal reflection
𝜔(𝑘)
𝜔 𝑐
=
𝑘 𝑛
𝑛𝑐𝑜𝑟𝑒
𝑛𝑐𝑙𝑎𝑑𝑑𝑖𝑛𝑔 < 𝑛𝑐𝑜𝑟𝑒
• Single defect: scattering
𝑘
• Periodic defects: band structure
𝑎
𝜔(𝑘)
• Band gaps – forbidden propagation
𝑘
𝜋
𝑎
Atom interactions around a band edge
• Consider atomic frequency near a band edge:
• Single atom (spontaneous emission):
• Enhanced near band edge due to high density of states (Γ1𝐷 ≫ Γ′)
Theory: S. John and T. Quang, PRA 50, 1764 (1994)
Expts with QD’s: M. Arcari et al, PRL 113, 093603 (2014)
Expts with atoms: A. Goban et al, Nature Commun. 5, 3808 (2014)
Atom interactions around a band edge
• Consider atomic frequency near a band edge:
physics
• Spontaneous emission shuts off (ideally), Im 𝐺 = 0
• Coherent interactions still remain! Re 𝐺 ≠ 0
S. John and J. Wang, PRB 43, 12772 (1991)
J.S. Douglas et al, Nature Photonics 9, 326 (2015)
Green’s function in bandgap
• What does the Green’s function 𝐺(𝑧, 𝑧 ′ , 𝜔) look like?
• From the outside, a photonic bandgap just looks like a
distributed Bragg reflector
• A source inside also produces an exponentially localized field
𝐺 𝑧, 𝑧 ′ , 𝜔 ∼ exp(− 𝑧 − 𝑧 ′ /𝐿) (inside bandgap)
Green’s function in bandgap
• Attenuation length L
• 𝐿 → ∞ as one approaches the band edge
• 𝐿 decreases as one moves deeper into the gap (limited by
diffraction to 𝐿 ∼ 𝜆)
• Near band edge, L is just determined by the band curvature
Spin model in a bandgap
• General spin model
𝑗
2
𝐻eff = −𝜇0 𝑑02 𝜔𝑒𝑔
𝑖
𝐺(𝑟𝑗 , 𝑟𝑖 , 𝜔𝑒𝑔 )𝜎𝑒𝑔
𝜎𝑔𝑒
𝑖,𝑗
Band gap
𝐻eff = 𝐴
𝑖,𝑗
𝑧𝑖 − 𝑧𝑗
exp −
𝐿
𝑗
𝑖
𝜎𝑒𝑔
𝜎𝑔𝑒
• Purely coherent interaction (no dissipation, at least ideally!)
• Tunable range of interaction L
• Now have all the ingredients to see coherent spin-motion
coupling
A sneak preview of the seminar…
Magnetism vs. crystallization
• Spin physics (encoded in electron spins) has been studied
forever
• “Quantum magnetism”
Curie Law 𝑴 ∝
𝑩
𝑻
• Can destroy paramagnetism at low temperatures, without
melting the material
• Physics of spin and crystallization have different origin and
different strengths (Bohr magneton vs. Coulomb)
Naïve question
𝑈 𝑥𝑖 − 𝑥𝑗 𝜎 𝑖 𝜎
𝐻eff ≈
𝑗
𝑖,𝑗
Mechanical potential
Leads to crystallization, etc.
Spin interactions
Leads to entanglement, etc.
• Can we create a crystal held together by spin entanglement?