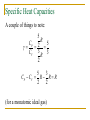Download Thermodynamics

Thermodynamics
Chapter 15
Expectations
After this chapter, students will:
Recognize and apply the four laws of
thermodynamics
Understand what is meant by thermodynamic
terms
Recognize and distinguish among four kinds of
thermal processes
Distinguish between reversible and irreversible
processes
Expectations
After this chapter, students will:
Analyze the properties and operations of heat
engines
Calculate the changes in entropy associated with
thermal processes
Thermodynamics: Some Fundamentals
Thermodynamics is the study of the economy of
heat energy and mechanical work, in the context
of the ideal gas.
Understanding thermodynamic concepts and
mathematical relationships depends on
understanding some terms.
Systems and Their Boundaries
In mechanics, we introduced the idea of the system:
a user-defined collection of objects.
In thermodynamics, “system” still means that.
However, we add the notion that the system will
usually include some definite amount of a fluid –
typically, an ideal gas. It might also include other
elements, such as the fluid’s container. It’s
always important to be clear about what’s in the
system, and what isn’t.
Systems and Their Boundaries
Once we have decided what the system is, we can
say that the surroundings consists of everything
that isn’t the system.
The system is separated from its surroundings by
walls. If the walls do not allow heat to pass
through them, they are adiabatic walls. If heat
can pass freely through the walls, we call them
diathermal walls.
The State of a System
The characteristics that tell us what we want to
know about a system define its condition, or state.
If the system consists of some amount of an ideal
gas, we’ll be interested in the temperature,
pressure, volume, and mass of the gas. Those
quantities are the state variables of the system.
Common Sense: 0th Law of
Thermodynamics
Suppose we have three systems: A, B, and C.
Suppose that A is in thermal equilibrium with C.
Suppose also that B is in thermal equilibrium with
C.
Then: A is in thermal equilibrium with B, and no
heat will flow between them if they are in contact.
(C is intended to be a thermometer.)
Energy Conservation: 1st Law of
Thermodynamics
Mathematical statement: DU  U f  U 0  Q  W
What does this mean?
DU is the change in the system’s internal energy
Uf is the system’s final internal energy
U0 is the system’s initial internal energy
Q is the heat added to the system
W is the work done by the system
Energy Conservation: 1st Law of
Thermodynamics
DU  U f  U 0  Q  W
Think of U as being the system’s bank balance, and
think of work and energy and heat as being forms
of cash. What we’ve said is that the change in the
system’s balance is its income (heat) minus its
spending (work).
Thermal Processes
A process is how the system, and its surroundings,
change from one state to another.
We’re going to consider four special cases of
thermal processes. These special cases help us to
understand what the laws of thermodynamics tell
us about systems and their properties.
Thermal Processes
In every case, we assume that the process occurs
“slowly.” The technical term for “occurs slowly”
is quasi-static.
What does “slowly” mean? It means that the system
has time to mix during the process. At all times,
we consider the temperature and the pressure of
the system to be uniform (the same in all places
throughout the system).
Isobaric Process
Isobaric: the pressure of the system is constant.
The result first:
W  P  DV  PV f  V0 
Why should this be?
Isobaric Process
Consider an ideal gas to which
heat is added.
W  F  S  PAS
But A·S = DV = Vf – Vi :
W  P  DV  PV f  Vi 
Isobaric Process
This process can be
represented graphically,
plotting pressure vs.
volume. Notice that the
work is the area under
this plot (P times DV).
Isochoric Process
Isochoric: the volume of the system is constant.
The result:
W 0
DU  Q  W  Q
Why? If volume is constant, nothing moves. No
motion, no work. Any heat added to the system
only changes its internal energy.
Isochoric Process
Pressure-volume plot for
an isochoric process:
No area under the plot
means no work is done.
Isothermal Process
Isothermal: the temperature of
the system is constant. Use the
ideal gas equation to write P as
a function of V: PV  nRT
nRT
P
V
Because P is not constant,
W  P  DV
Isothermal Process
The work is still the area under
the isotherm plot. To calculate
it, we integrate:
Vi
nRT
W
dV
V
Vf
(natural log)
 Vf
W  nRT ln 
 Vi



Adiabatic Process
In an adiabatic process, no heat
enters or leaves the system:
Q = 0. The First Law becomes:
DU  Q  W  W
But, as we learned in chapter 14,
3
U  nRT
2
(for a monatomic ideal gas).
Adiabatic Process
3
3
If U  nRT , then DU  nRDT
2
2
and
DU  Q  W  W
3
3
so W   nRDT  nRTi  T f 
2
2
3
W  nR Ti  T f 
2
(monatomic ideal gas)
Adiabatic Process
Notice that the adiabatic curve is
different from both isotherms
(corresponding to the initial and
final temperatures).

Its equation is: PiVi  Pf V f
cP
where  
cV

specific heat capacity @ constant pressure
specific heat capacity @ constant volume
Specific Heat Capacities
Define a molar specific heat capacity, C, for an
ideal gas: Q = C n DT
(SI units: J / mol·K)
First Law: DU  Q  W  Q  DU  W
At constant pressure (isobaric):
W  P DV  PV f  Vi 
Specific Heat Capacities
Substitute for Vi and Vf from the ideal gas equation:
nRT
V
P
W  PV f  Vi   nRT f  Ti 
3
For a monatomic ideal gas: DU  nRT f  Ti 
2
Substitute:
3
5
Q  DU  W  nRT f  Ti   nRT f  Ti   nR T f  Ti 
2
2
Specific Heat Capacities
5
5
Q  nRT f  Ti   nRDT
2
2
Equate this expression for Q to the one from our
defining equation for molar heat capacity:
5
5
Q  nRDT  CnDT  CP  R
2
2
Specific Heat Capacities
At constant volume (isochoric):
W 0
3
Q  CnDT  DU  W  nRDT
2
3
CV  R
2
Specific Heat Capacities
A couple of things to note:
5
R
CP 2
5



CV 3 R 3
2
5
3
CP  CV  R  R  R
2
2
(for a monatomic ideal gas)
Second Law of Thermodynamics
Heat flows spontaneously from regions of higher
temperature to regions of lower temperature. It
does not flow spontaneously in the other
direction.
Set your cup of hot coffee down on the sidewalk
tonight. Come back and get it in after a few
minutes. It won’t be hotter.
Second Law and Heat Engines
As heat flows from a hotter region
to a colder one, a device can be
constructed that will use some of
that heat to do mechanical work.
Such a device is called a heat
engine.
Heat Engines
A familiar example: internal
combustion (auto) engine.
Hot reservoir: burning fuel-air
mixture
Cold reservoir: exhaust gases
Heat Engines: Energy Conservation
The principle of energy
conservation requires:
QH  W  QC
Heat Engines: Efficiency
Efficiency is defined as the ratio
of the work done by the heat
engine to the input heat it
receives.
W
QH  QC
QC
e

1
QH
QH
QH
Efficiency is a dimensionless,
unitless ratio.
Efficiency and Reversibility
A process is called reversible if both the system
and its environment can be returned, after the
process, to exactly the same states they were in
before the process.
irreversible
reversible
Efficiency and Reversibility
No process involving friction is reversible.
Also, any process in which heat flows
spontaneously from a hot to a cold reservoir is
irreversible. The system can be restored to its
original state, but the work required changes the
environment further from its original state.
Carnot’s Principle
No irreversible heat engine operating between two
reservoirs at constant temperatures can be more
efficient than a reversible engine operating
between the same temperatures. All reversible
engines operating between the same two
temperatures have the same efficiency.
Sadi Nicolas Leonard Carnot
1796 – 1832
French military engineer
Efficiency of a Carnot Engine
If a thermodynamic temperature scale is correctly
defined, the ratio of the heat into the cold reservoir
to the heat from the hot reservoir is equal to the ratio
of the reservoir temperatures:
QC TC

QH TH
Lord Kelvin defined his thermodynamic temperature
scale so that this is true. The temperatures in the
above equation must be absolute (in Kelvins).
Efficiency of a Carnot Engine
Earlier, we said that the efficiency of a heat engine
is
QC
e 1
QH
TC
Substituting from the previous equation: eC  1 
TH
This is true for a Carnot engine. Notice that we are
assuming that the reservoir temperaures are not
changed by the operation of the engine.
A Different Kind of Reversibility
A heat engine diverts some of the heat flowing
spontaneously from hot to cold, and uses it to
generate output work.
If we are willing to input work, then we can cause
heat to flow from cold to hot. (Heat pump,
refrigerator.) Notice that this reverse operation is
not the same thing as thermodynamic
reversibility.
Heat Pumps and Refrigerators
Conservation of energy applies to heat pumps as
well as to heat engines: QH = W + QC
For a thermodynamically-reversible heat pump or
refrigerator:
QC TC
QH

TH
Refrigerator: coefficient of performance
QC
coeff. of performanc e 
W
Entropy
Entropy: the loss of our ability to use heat to
perform work, because of the irreversible
spontaneous flow of heat from higher to lower
temperatures.
If heat flows into or out of a system reversibly, the
system’s change in entropy is
Q
DS 
T
SI units: J / K
Entropy and Reversible Engines
The change in entropy associated with the
operation of a Carnot engine:
hot reservoir
 QH
DS H 
TH
cold reservoir
QC
DSC 
TC
QC  QH QC QH



total change: DStotal 
TC
TH
TC TH
Entropy and Reversible Engines
But Carnot’s principle said that
QC TC
QC QH



QH TH
TC TH
So, the total change in entropy associated with the
operation of a Carnot engine is
QC QH QC QC
DStotal 



0
TC TH
TC TC
So: the operation of a reversible engine does not
change the total entropy of the universe. Irreversible
processes increase the entropy of the universe.
Energy Unavailable for Doing Work
Consider a reversible engine working between
reservoir temperatures of 650K and 150K.
Its efficiency:
TC
150 K
eC  1 
1
 0.769
TH
650 K
If 1200 J of heat are drawn from
the hot reservoir, the work is
W  eQH  0.7691200 J   923 J
Energy Unavailable for Doing Work
Now we provide a path for our
1200 J of heat to flow
irreversibly from the 650K
reservoir to a cooler one, at
350K. Now our engine’s
efficiency becomes:
TC
150 K
eC  1 
1
 0.571
TH
350 K
Energy Unavailable for Doing Work
At this decreased efficiency, the
work done by this 1200 J of heat
is:
W  eQH  0.571 1200 J   685 J
The work done by this heat in
descending from 650 K to 150 K
has decreased by 923 J – 685 J,
or 238 J.
Energy Unavailable for Doing Work
We can also calculate this loss of
work by calculating the
increase in the entropy of the
universe associated with the
irreversible part of the heat
flow:
Q350K
Q650K
DSuniverse 

350 K 650 K
1200 J  1200 J


 1.582 J/K
350 K
650 K
Energy Unavailable for Doing Work
Then apply Eq. 15.19 from your
textbook to calculate the
energy unavailable for work:
Wunavailable  T0 DSuniverse
Wunavailable  (150 K)1.582 J/K   237 J
The irreversible flow causes this.