Download A - Basics of electronic structure and Molecular bounding (Diatomic

A - Basics of electronic structure
and
Molecular bounding
(Diatomic molecules)
Chapter 1
Basics of electronic structure
The properties of molecules are basically determined by their orbitals, whose
electronic wave functions are built up of the electronic wave functions of the
atoms which comprise the molecule. The compendium begins with a short
review of atomic wave functions, and then outlines the LCAO molecular orbitals for the simplest molecule, H+
2 . The presentation intends to provide
basic material for understanding the method, so instead of making a thorough treatment of all terms in the Schrödinger equation, references to more
complete sources are given.
• Atomic orbitals can be written as a product of angular and radial wave
functions
χnlm = Am
(1.1)
l (θ, φ) · Rnl (r),
where θ and φ are the azimuthal and equatorial space angles and r is
the distance between the electron and the nucleus. n, l, and m are the
principal, the angular momentum and the magnetic quantum numbers,
respectively, that are known from the hydrogen atom.
• The energy order of atomic orbitals is 1s < 2s < 2p < 3s < 3p < 4s <
3d . . . In the ground states the orbitals are occupied in this order with
electrons. The energy order is in first approximation given by
1. the principal quantum number (i.e. the energy order of the atomic
orbitals in the hydrogen atom) .
2. orbitals with lower angular momentum quantum number generally penetrate the region close to the nucleus. In this region the
attractive potential between the negatively charged electrons and
the positive nuclei is less shielded by electrons. Thus the energies
of orbitals with the same principal quantum number increase with
the angular momentum quantum number.
1
Table 1.1: Spherical harmonics (Ylm ) in angular coordinates and real harmonics (Slm ) in angular and Cartesian coordinates
Y00
Y10
Y11
Y1−1
Y20
Y21
Y22
Y2−1
Y2−2
Spherical
Harmonics
q
1
q 4π
3
cos(θ)
q 4π
3
− 8π sin(θ)eiφ
q
3
sin(θ)e−iφ
q 8π
5
(3 cos2 (θ) − 1)
q 16π
5
− 8π
cos(θ) sin(θ)eiφ
q
5
cos(θ) sin(θ)e2iφ
q 8π
5
cos(θ) sin(θ)e−iφ
q 8π
5
cos(θ) sin(θ)e−2iφ
8π
q
Real Harmonics
q
1
q 4π
3
cos(θ)
q 4π
3
sin(θ) sin(φ)
q 4π
3
sin(θ) cos(φ)
q 4π
5
(3 cos2 (θ) − 1)
q 16π
5
cos(θ) sin(θ) cos(φ)
q 4π
5
sin2 (θ) cos(2φ)
q 4π
5
cos(θ) sin(θ) sin(φ)
q 4π
5
sin2 (θ) sin(2φ)
4π
S00
S10
S11
S1−1
S20
S21
S22
S2−1
S2−2
1
s
q 4π
3 z
pz
q 4π r
3 x
q 4π r
3 y
q 4π r 2 2
5 3z −r
q 16π r2
5 xz
q 4π r22 2
5 x −y
q 4π r2
5 yz
q 4π r2
5 xy
4π r 2
3. In the nonrelativistic approximation orbitals are 2l + 1 fold degenerate (m = −l, −l + 1, . . . , l − 1, l). The electrons also have
spin so orbitals with l 6= 0 are further split due to the relativistic
spin orbit interaction. In the one electron “orbital” picture each
nl level is split into the 2l +2 (2l) fold degenerate states with total
momentum j = l + 1/2 (j = l − 1/2).
For the radial wave function in equation (1.1) several different representations are possible. It is often convenient to use either numerical functions
or to employ a linear combination of Slater type orbitals
χl,Slater (r) = N · rl+n · exp(−ζ · r),
(1.2)
where N is a normalization constant. The exponent ζ and the integer n
(n ≥ 0) are chosen to optimize the properties of the wave function.
The best known form of the angular wave functions in equation (1.1) are
the spherical harmonics (Table 1.1). These functions are complex making all
basis functions and integrals complex. Therefore, the real harmonics (also
displayed in Table 1.1) are generally used in molecular calculations. Apart
from calculational advantages these real functions are also much easier for
interpretation purposes. A quick inspection of Table 1.1 will show you that
the full m set of spherical and real harmonics both span the same functional
space.
2
px
py
dz2
dxz
dx2 −y2
dyz
dxy
Figure 1.1: Distances occuring in the Hamiltonian of H+
2
1.1
The H+
2 molecule
This molecular ion is the simplest system, and is useful to illustrate the principles of chemical bonding. We apply the Born-Oppenheimer approximation1
1.2
Basic equations
Then the Schrödinger equation
ĤΨ = EΨ
(1.3)
of this system with the Hamiltonian in atomic units2
∂2
∂2
∂2
1
1
1
+
+
−
−
+ .
2
2
2
∂x
∂y
∂z
R1 R2 R
!
1
Ĥ = −
2
|
{z
(1.4)
}
∆
The distances R1 , R2 and R are given in Fig. 1.1.
1
This means, we do not treat the nuclear motion, but only the wave function of the
electrons (electronic wave function) in the field of the nuclei that are “fixed in space”. In
other words we consider the electrons to be infinitely faster than the nuclei. We use the
obtained electronic energy as the potential of the molecule.
2
Atomic units are defined by h̄ = e = me = 1/4π0 = 1. So 1 au is at the same time
a measure for energy 1au = 4.359 743 81(34)×10−18 J = 27.211383 eV = 219474.6354
cm−1 = 2625.5002 kJ/mol; for length 1au that is also called one Bohr 1a0 = 0.529 177
2083(19) Å; for time 1au = 2.418 884 326 500(18)×10−17 sec; for mass 1au = 9.109 381
88(72)×10−31 kg. See e.g. http://physics.nist.gov/cuu/Constants/index.html for
more information.
3
Consider the ground state of this molecule and use an approximate
wave function that allows a simple interpretation and generalization of the
results.3
1.3
The MO-LCAO ansatz (matrix equations)
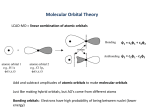
We build up the orbitals using the “molecular orbitals as linear combinations
of atomic orbitals” (MO-LCAO) ansatz. We can write the molecular orbital
ϕi
ϕi = c1i χ1 + c2i χ2 ,
(1.5)
where the cµi are coefficients and the χµ are the hydrogen-like 1s basis functions at the H atom µ
s
ζ3
exp(−ζRµ ).
(1.6)
χµ =
π
Hydrogen-like basis functions have ζ = 1, but they may be improved in a
number of ways. In fact a change of ζ is the simplest and most efficient way
to do this. The ζ parameter influcences the distribution of charge in the
hydrogenic orbital.
By plugging equation (1.5) into the Schrödinger equation (1.3), multiplying from the left with χµ and integrating over all space, we obtain a linear
system of equations
(χ1 |Ĥ|χ1 )c1 + (χ1 |Ĥ|χ2 )c2 = E [(χ1 |χ1 )c1 + (χ1 |χ2 )c2 ]
(χ2 |Ĥ|χ1 )c1 + (χ2 |Ĥ|χ2 )c2 = E [(χ2 |χ1 )c1 + (χ2 |χ2 )c2 ] .
(1.7)
Using
H11 = (χ1 |Ĥ|χ1 ) = (χ2 |Ĥ|χ2 )
H12 = (χ1 |Ĥ|χ2 ) = (χ2 |Ĥ|χ1 )
1 = (χ1 |χ1 ) = (χ2 |χ2 )
S = (χ1 |χ2 ) = (χ2 |χ1 ),
(symmetry)
(Hermicity of Ĥ)
(normalization)
(definition)
(1.8)
(1.9)
(1.10)
(1.11)
we come to the matrix equation
H11 H12
H12 H11
!
c1
c2
!
=E
3
1 S
S 1
!
c1
c2
!
,
(1.12)
One of the big problems in quantum mechanics is that the only accurate solutions to
the Schrödinger equation are numerical. Nevertheless, a comparison to the exact solution
may be of interest. This may be found in H. Wind, J. Chem. Phys. 42, 2371 (1965) (1σg
i.e. the ground state) and J. M. Peek, J. Chem. Phys. 43, 3004 (1965) (1σu state of the
hydrogen ion).
4
that can be easily solved to
E1/2 =
H11 ± H12
,
1±S
(1.13)
with the eigenfunctions
1
ϕ1/2 = q
(χ1 ± χ2 ).
2(1 ± S)
The √
1
2(1±S)
(1.14)
terms are normalization constants. They result from the fact
that the basis functions are nonorthogonal. Since the H+
2 molecule has cylindrical symmetry the wave functions must be symmetric with respect to each
atom, so this result is not surprising. The two eigenfunctions ϕ1 and ϕ2 are
the odd and even combinations of the Slater orbitals, with symmetries σg
and σu .
For homonuclear diatomic molecules the orbitals can be classified by symmetry using the German terms gerade and ungerade. The internuclear axis
(R) is the symmetry axis, and the midpoint of the axis is the center of symmetry. Thus an inversion of wave function coordinates is made with respect
to this point (ri → −ri ). Those which are unaltered after this transformation
are even functions gerade while those which change sign, the odd functions,
are called ungerade. Thus for this class of molecules (symmetry group) the
electronic states corresponding to the orbitals are denoted as Σg , Σu , Πg , Πg .
Further indicies can indicate the parity of the orbital (+ or -).
The molecular orbital extends over the entire molecule; thus the wave
function is delocalized. Note that the value of the wave function at the
position of the atoms changes with the bond distance.
To understand the results of the preceeding calculation, we first have to
solve the matrix elements in equation (1.12). These can be obtained to be4
!
H11 =
H12 =
S =
where % = ζR. We
1
1 2
ζ −ζ +ζ 1+
exp(−2%)
(1.15)
2
%
" #
1 1
1 2
1
5
ζ ζ
+ % − % + − 1 − % exp(−%)
(1.16)
2 2
6
%
3
1 2
1 + % + % exp(−%),
(1.17)
3
consider only ζ = 1 so the matrix elements become
1
1
H11 = − + 1 +
exp(−2R)
2
R
4
(1.18)
See e.g. H. Hellmann: Einführung in die Quantenchemie, Deuticke, Leipzig 1927 or
C. C. J. Roothan, J. Chem. Phys. 19, 1445 (1951).
5
1 7
1
1
− − R − R2 exp(−R)
H12 =
R 2 6
6
1 2
S = 1 + R + R exp(−R).
3
(1.19)
(1.20)
For a qualitative interpretation of the eigenvalues it is useful to rewrite them
as
H11 + H12
H12 − SH11
β
= H11 +
= H11 +
1+S
1+S
1+S
H11 − H12
H12 − SH11
β
=
= H11 −
= H11 −
.
1−S
1−S
1−S
E1 =
(1.21)
E2
(1.22)
The β is called the reduced-resonance integral, and S is the overlap integral.
These integrals can be evaluated after the wave functions are determined.
Exercise 1
Write down the energy expression in terms of the solved integrals. In the
first exercises set the effective charge equal to 1. Set up the equations in
MatLab and solve them.
1. Plot the matrix elements as a function of R in one graph, and the
gerade and ungerade potentials as a function of R in another. The
overlap wavefunction S is very important in bonding–note that the
overlap integral is substantial at the equilibrium bond distance. It is
even larger for neutral H+
2 . β describes the chemical bond in E1 rather
1
realistically as H11 ≈ − 2 , although it overshoots due to the overlap in
equation (1.21).
2. Determine the lowest energy of the gerade and ungerade states from
the potential energy curves.
3. Determine the dissociation energy of the bound state, and the internuclear distance corresponding to the minimum of the bound state.
4. The experimental equilibrium bond length for H+
2 is 2.003 a.u., and the
dissociation energy is 0.102 a.u. How do these values compare to the
values derived from the calculation? In the next section we will work
on improving the model to get better agreement with experiment.
The reduced resonance integral β has the important property that it
describes the chemical bonding as a function of R. In fact in some semi
empirical methods it is used as an adjustable parameter representing
6
the chemical bonding. In these cases one typically assumes that H11 =
α = const.
5. Plot the eigenenergies for the bound state, first for ζ = 1, then for a
few other values both larger and smaller than 1.
6. Find a value of ζ which produces improved values for the calculated
dissociation energy, and for the internuclear distance. This can be done
by trial and error, testing different effective charges and looking at the
derivative of the potential energy function to get the minimum, or by
analytical methods. What value of the effective charge produces the
best value for the dissociation energy and the internuclear distance?
7. Using the potential from the previous problem estimate the vibrational frequency of the bound state of the hydrogen molecular ion. This can be done
by approximating the deepest part of the potential well by a harmonic oscillator function.
of a chemical bond within this
p The vibrational2 frequency
2
model is ω = k/µ where k = (d E/dR ) is the force constant, and µ is the
reduced mass of the molecule. m(1 H)=1.0078 u.
1.4
Quasi classical and interference contributions to the chemical bond
Can we construct a similar picture of chemical bonding using a quasi-classical
picture? Let’s try to calculate the energy of the system
H
+
H+
(1.23)
H+
+
H
(1.24)
or
.
In order to conserve the symmetry of the system we consider a fifty-fifty
mix of these alternatives. Then the quasi classical density ρQC of the system
is
1
ρQC (~r) = (ρ1 (~r) + ρ2 (~r)) ,
(1.25)
2
where ρ1 is the ground state density of hydrogen atom 1. As the density ρ1
is exactly that generated by the wave function
ϕ = χ1
i.e. ρ1 = χ21 ,
7
(1.26)
the energy of this system is given simply by H11 .
Now we consider the MO-LCAO density of a molecule
ρLCAO =
1
χ21 + 2χ1 χ2 + χ22 .
2(1 + S)
(1.27)
The interference term 2χ1 χ2 is connected to the H12 and β terms in equation
(1.21) in the ground-state energy. These imporant parameters are responsible
for the bond.
It should be stated that the overlap plays a somewhat ambiguous role:
From equation (1.21) we can see that the overlap integral reduces the size of
the chemical bond. So the overlap can be considered to be an antibonding
effect. We will see in the following section that this is mostly due to the
reduction of the size of the wave function at the nuclei. On the other hand
the bond occurs if and only if there is an overlap between the atomic orbitals,
thus the overlap term (nondiagonal) is also responsible for the bond.
1.5
What is the reason for chemical bonding?
The densities of the quantum mechanical and classical pictures are shown
in Figure 1.2. We recognize that interference increases the probability of
finding the electron between the two hydrogen atoms. The bonding orbital
has a substantial probability for the electron to be between the nuclei while
this probability goes to zero for the antisymmetric case.
In reality the chemical bonding as we have discussed it so far causes an
increase of the potential energy, rather than the decrease that one would
expect. This is shown in Figure 1.3. Clearly the reduction of density in the
region close to the nuclei overcompensates the energy gain from the increased
density between the hydrogen atoms. The Figure shows that a decrease in
kinetic energy is responsible for the lower energy.
The MO-LCAO picture does not reproduce the kinetic and potential energy distributions although this model provides a qualitative description of
the bonding. The correct density, which is also shown in Figure 1.2 is also
higher near the nuclei than close to the atom. Implementation of this density
results in a potential energy which is lower at the ground-state internuclear
distance than for the dissociated system (Fig. 1.4). In fact one should say
that this result is expected since for a stable orbit in a Coulombic system the
virial theorem holds requiring that
1
V = −T = E.
2
8
(1.28)
Figure 1.2: Densities of the ground state 1σg (a) and the first excited state 1σu
(b) of H+
2 molecule in different approximations: The LCAO approximation
(dashed line), the quasi classical approximation (dashed dotted line), and
from the exact wave function (full line).
Chemical bonding arises from a reduction of the kinetic energy after taking
into account the contributions of H11 and β. The decrease in potential energy
is due to its reduction in H11 . β describes the bonding and leads to a positive
potential energy and a negative kinetic-energy contribution.
9
Figure 1.3: The total energy E = E1 of the H+
2 ion in its ground state
according to the MO-LCAO Ansatz. Also the contributions of the kinetic
and potential energy (T and V ) are shown.
1.6
Local and nonlocal properties of H+
2
In terms of the wave function and its density there are some subtle points to
be considered. The two protons each contain half an electron on the average.
We could naively assume that each of the hydrogen atoms has a charge of
+ 12 and, at long range distances, we should get an interaction energy that
goes as
+ 12 + 12
1
=
.
(1.29)
R
4R
10
Figure 1.4: The total energy E = E1 of the H+
2 ion calculated from an exact
wave function. The separate contributions from the kinetic and potential
energies (T and V ) are given.
Instead for the asymptotic limit the MO-LCAO Ansatz yields
2
1
1
lim E1 = − + exp(−R) − R +
+ O(exp(−2R).
(1.30)
R→∞
2
3
R
So although the wave function is delocalized in the entire geometry space
the observable, energy, shows no other long-range behaviour than we would
expect for a completely localized system (H + H+ ). On the other hand, this
is not the case near the equilibrium bond distance, where there is substantial
overlap. Here the chemical bond, which is indeed a delocalization effect,
makes a significant difference in the energy.
11
1.7
Summary
We have used the example of the H+
2 molecule and found that:
• The chemical bonding can be described qualitatively correctly with
the MO-LCAO ansatz. This transforms the Schrödinger equation into
a matrix equation.
• We discussed the somewhat ambiguous role of the overlap. We found
that the overlap itself reduces the strength of the bond but since overlap is necessary to make the interference effect possible, the general
statement: “positive overlap causes an increase of bonding” is correct.
In any case it is important to note that the overlap is not a small effect
that can be neglected. The size of the overlap integral S is on the order
of 0.8 − 0.5.
• For each bonding orbital a corresponding antibonding one exists. We
also saw that due to the overlap integral the antibonding effect of the
antibonding orbital is always stronger than the bonding effect of the
bonding orbital.
• Another effect of the overlap is to pull the wave functions away from the
nuclei. In the H+
2 molecule this is compensated by the extraordinarily
strong relaxation of this orbital. In other molecules this is not the case.
1.8
Exercises
1. Calculate the (a) eigenvalues and (b) eigenvectors of the equation system
!
H11 − E
H12 − S · E
~c = ~0,
(1.31)
H12 − S · E
H11 − E
by (a) finding the two values of E for which the determinant
H −E
11
H12 − S · E
H12 − S · E
H11 − E
.
(1.32)
becomes zero and (b) by inserting these energies in equation (1.31).
2. What is the ground state energy of a particle with mass m in
a) a box with length l,
b) a box with length 2l,
12
c) two separate boxes with the length l?
All boxes are assumed to be only one dimensional and to have infinite
energies outside the box. Is there a difference between the energy of
localized and delocalized solutions of case c?
How are these systems related to possible wave functions/geometries
of the H+
2 molecule?
13
Chapter 2
More than one electron: H2
2.1
Molecular orbitals
The hydrogen molecule is the next simplest illustrative system; it has one
additional electron. We use the same molecular orbitals obtained for the H+
2
system.
1
ϕ1 = q
2(1 + S)
1
ϕ2 = q
2(1 − S)
2.2
(χ1 + χ2 )
:
σg
(2.1)
(χ1 − χ2 )
:
σu .
(2.2)
Many electron wave functions: inclusion
of electron spin
In accord with the Pauli principle the electrons must be in unique orbitals.
We will go through the H2 neutral molecule, a system with two electrons.
Since electrons are fermions (S = 21 ) the wave function must be antisymmetric with respect to exchange of the electrons. The wave function cannot have
two electrons in the same orbital. The most common solution for this is to
set up the wave function as a Slater determinant. The ground state of H2
will have two electrons in the lowest orbital ϕ1 . A trial wave function with
spin orbitals α and β where the two electron wave function is written as a
product of a spatial and a spin part:
Φ1
1 ϕ (r ) ϕ̄1 (r1 )
= √ 1 1
2 ϕ1 (r2 ) ϕ̄1 (r2 )
14
≡ |ϕ1 ϕ̄1 |
(2.3)
Figure 2.1: Distances appearing in the Hamiltonian of the H2 molecule.
1
= √ [ϕ1 (r1 )ϕ̄1 (r2 ) − ϕ1 (r2 )ϕ̄1 (r1 )]
2
1
= √ ϕ1 (r1 )ϕ1 (r2 ) [α(1)β(2) − α(2)β(1)] .
{z
}|
{z
}
2|
spin
part
spatial part
(2.4)
(2.5)
Here the bar indicates an orbital with a β spin orbital. The index i refers
to the electron, ri is the position of electron i. For the case of a singlet wave
function the spatial part of the wave function is symmetric, whereas the spin
part is antisymmetric. The triplet wave function has an antisymmetric wave
function with symmetric spin.
2.3
Energy expectation values
In the Hamiltonian we now have to consider the distances shown in Fig. 2.1
and we obtain
1
1
1
1
1
1
1
1
Ĥ = − ∆1 −
−
− ∆2 −
−
+ +
.
2
R11 R21 2
R12 R22 R r12
(2.6)
If we compare the Hamiltonian with the one from the H+
2 molecule [Eq. (1.4)],
then it becomes clear that the equation above may be rewritten to
Ĥ = ĥ1 + ĥ2 −
15
1
1
+
,
R r12
(2.7)
with hi being the Hamiltonian from Eq. (1.4) acting on electron i. This
result is particularly useful for the next step in which we want to calculate
the energy expectation value
hEi =
hΦ1 |Ĥ|Φ1 i
hΦ1 |Φ1 i
(2.8)
of the wave function from Eq. (2.3). As the molecular orbitals are normalized,
this expectation value can be evaluated according to the Slater-Condon rules1
to
1
hEi = 2(ϕ1 |ĥ|ϕ1 ) − + (ϕ1 ϕ1 |ϕ1 ϕ1 ),
(2.9)
R
where
(ϕi ϕj |ϕk ϕl ) =
Z Z
ϕ∗i (r1 )ϕj (r1 )
1
ϕk (r2 )∗ ϕl (r2 )dr1 dr2 .
r12
(2.10)
We see that the first matrix element in Eq. (2.9) is identical to the ground
state energy of the H2+ molecule in the MO-LCAO approximation. The
second term is the nuclear repulsion and the last term is the two-electron
integral Coulomb.
2.4
Potential energy curves
The integrals are not evaluated analytically here, but the matrix elements
will be investigated. The energies are plotted in Fig. 2.2. From this we see
that the MO-LCAO method is quite reasonable for short bond distances R.
At large distances there are some problems. We expect the energy to be equal
to that of the two separated atoms, 1 Hartree. The plot shows that instead
5
11
Hartree. The error of 16
Hartree corresponds
the energy converges to − 16
to 8.5 eV, which is about twice than the bonding energy of H2 (4.5 eV). The
error is the same order of magnitude as the ionization potential of H2 (16
eV).
This rather astonishing result can be made plausible if we rewrite the
spatial part of the wave function in Eq. (2.5) in terms of the atomic orbitals
[Eq. (2.4)]
Φ1 = ϕ1 (r1 )ϕ1 (r2 )
1
See e.g. F. L. Pilar, Elementary quantum chemistry (McGraw-Hill, New York, 1990),
A. Szabo and N. S. Ostlund, Modern Quantum Chemistry: Introduction to Advanced
Electronic Structure Theory (McGraw-Hill, New York, 1989), R. Mc Weeny, Methods of
molecular quantum mechanics (Academic Press, London, 1996).
16
Figure 2.2: Energy of the H2 molecule according to the MO-LCAO ansatz.
The contributions to this, i.e. the energy of the H+
2 molecule and the difference between the electron electron repulsion and the negative of the nuclear
attraction energy, are also shown.
1
(χ1 (r1 ) + χ2 (r1 )) q
(χ2 (r2 ) + χ2 (r2 ))
(2.11)
2(1 + S)
2(1 + S)
h
i
1
=
χ1 (1)χ1 (2) + χ1 (1)χ2 (2) + χ2 (1)χ1 (2) + χ2 (1)χ2 (2) .
{z
} |
{z
} |
{z
} |
{z
}
2(1 + S) |
•
•
•
•
−
+
+
−
H +H
H +H
H +H
H +H
=q
1
Here H+ , H• , and H− designate protons, hydrogen atoms, and hydrogen
anions, respectively. For R → ∞ it is clear that the two particle wave
17
function in Eq. (2.11) represents only for 50% the desired hydrogen atoms,
whereas 50% of the wave function correspond to the energetically much higher
ionic compounds (H+ + H− ).
2.5
Correction of the erroneous dissociation
behaviour
A solution to this problem can be found by considering the Slater determinant
with the σu MOs ϕ2
h
i
1
χ1 (1)χ1 (2) − χ1 (1)χ2 (2) − χ2 (1)χ1 (2) + χ2 (1)χ2 (2) .
{z
} |
{z
} |
{z
} |
{z
}
2(1 − S) |
•
•
•
•
−
+
+
−
H
+
H
H
+
H
H +H
H +H
(2.12)
It is clear that this Slater determinant itself contains the same problem as
the one in Eq. (2.11), but a linear combination of these
Φ2 = ϕ(r1 )ϕ2 (r2 ) =
Ψ = c 1 Φ1 + c 2 Φ2 ,
(2.13)
with c1 = −c2 = √12 gives the correct dissociation properties. Unfortunately
this means that a realistic description of the electronic wave function of H2 already needs the configuration interaction (CI) description given in Eq. (2.13).
This is a much more involved representation of the electronic wave function
than that given by the simple Slater determinant in Eq. (2.3–2.5)
2.6
Conclusions
Figure 2.3 shows that if one considers only properties near to the ground
state geometry of the H2 molecule then the MO-LCAO picture is in fact
not too bad. It does describe the equilibrium bond distance of the molecule
quite well and even the much more elaborate CI wave function does not give
a substantial improvement of the energy. As discussed before this changes
if we consider longer bond distances. There, the CI potential energy curve
becomes exact, whereas the MO-LCAO curve shows the wrong asymptotic
behaviour discussed above.
Nevertheless, there remains a big error left that we didn’t manage to treat
in this methods. This error is composed of two things. Firstly, as in the case
of H+
2 , a change of the orbital form (relaxation) would cause a decrease of
the energy. Secondly, we now consider the problem of two different electrons
that repel each other. Nevertheless, the wave function does not provide a
18
Figure 2.3: Potential energy curves of H2 calculated with the MO-LCAO
ansatz, a CI wave function and the “exact” solution.
possibility for the electrons to avoid positions in which they are near to the
other one. The fact that electrons do this is one of the major mistakes of the
MO-LCAO description and also of the more general Hartree-Fock self consistent field (HF-SCF) method. It is generally designated as dynamic electron
correlation as it has to do with the dynamics of the electronic motion in cases
when it is fast. The failure of Hartree Fock to describe the dissociation is
designated as static electron correlation, for it has to do with the fact that
for a long bond distance the (infinitely slow = static) electronic motion is
not properly described.
19
Chapter 3
Diatomic molecules (bonding
and nonbonding properties)
3.1
Correlation diagram (for homonuclear molecules)
In Figure 3.1 a correlation diagram for homonuclear diatomic molecules is
shown. Contrary to the form that may be found in ordinary textbooks, both
atomic levels are not shown here. It is probably not a severe problem to
see that the interactions are due to bonding and antibonding interactions of
orbitals as shown before in Fig. ??. Only the atomic levels on the left side
are shown here. Two levels of interactions are indicated which are important
for getting insight in the bonding and antibonding properties of the orbitals.
In the first level of interaction only the splitting due to the interactions of
equal orbitals (e.g. 2s1 –2s2 ) are taken into account. This gives already a good
qualitative picture. The two 1s orbitals have only a very weak interaction
and give rise to the 1σg and 1σu orbitals. In general the splitting of these
orbitals is clearly below 0.1 eV and not detectable.1 Due to the small splitting
of the two 1s orbitals one should state that these orbitals are nonbonding in
their nature. Nevertheless, if electrons are taken out from these core orbitals
this often has a big effect on the bonding properties. See e.g. exercise 5 in
this chapter. It should be emphasized that this effect is not due to a simple
bonding/antibonding classification of these orbitals.
The two 2s orbitals have a much stronger interaction and cause the existence of the bonding 2σg and the antibonding 2σu orbitals. The 2p orbitals
1
An exception from this is the Ethin (Acetylene) molecule, in which the short bond
length 1.15 Å together with the relative big 1s orbital causes a splitting of 105±10 meV.
For further details see B. Kempgens, H. Köppel, A. Kivimäki, M. Neeb, L. S. Cederbaum,
and A. M. Bradshaw, Phys. Rev. Lett. 79, 3617 (1997).
20
Figure 3.1: Correlation diagram for homonuclear diatomic molecules that
consist of two first row (Li–Ne) atoms.
generate two types of interactions. The stronger bonding/antibonding interaction is due to the 2pσ orbitals, the weaker one due to the 2pπ orbitals.
These give rise to the bonding/antibonding 3σg /3σu and 1πu /1πg molecular
orbitals, respectively.
A more detailed inspection of Fig. 3.1 shows that further interactions are
21
possible in this system due to the fact that the 2σg and 3σg as well as the
ungerade orbitals have the same symmetry. This causes that the character
of the 2σg orbital is in fact very strongly bonding, whereas the binding properties of the 3σg orbital are only moderate. In fact the latter orbital turns
out to be for most of these molecules rather nonbonding, but it has a very
weak bonding effect. Analogously, the strong antibonding character of the
2σu orbital is mostly transferred to the 3σu orbital so that the 2σu orbital
may also be considered as nonbonding. The 3σu orbital is so strongly antibonding that it is for most diatomic homonuclear molecules far above the
ionization threshold, where it gives rise to the so called σ resonances.2 Due
to the strongly antibonding character of the 3σu orbital the occupation of
it is energetically extremely unfavourable and leads to a rapidly dissociating
electronic state.
Apart from this effect on the bonding character of the orbitals, the mixing
of the σg,u orbitals also has an important effect on the energetical order of the
orbitals. The interaction between the 2σg and 3σg orbitals lifts the energy
of the latter to a point that is very near to the energy of the 1πu orbital. In
most of the cases the 3σg orbital lies energetically even higher than the 1πu .
Furthermore, the 2σu orbital is energetically clearly below these two.
These bonding properties can be summed up as indicated in Fig. 3.1.
These more qualitative statements can be verified with the accurately known
equilibrium bond distances and vibrational frequencies of some of these homonuclear diatomic systems. In Table 3.1 this is shown at the example of the
spectroscopic constants of the ground states of neutral N2 and O2 and some
of their lowest ionised states. We clearly see the antibonding property of the
1πg orbital on the much bigger equilibrium bond distance of O2 as compared
to N2 and on the decrease of the bond distance of O2 as compared to its its
lowest cation. The mostly nonbonding but very slightly bonding character
of the 3σg orbital is seen from the slight increase of re for X → X̃ ionization in N2 and for X → b̃ ionization in O2 . The moderately strong bonding
character of the 1πu orbital is seen from the increase of re for ionization to
the à and ã state of N2 and O2 , respectively. Also the mostly nonbonding,
but slightly antibonding character of the 2σu orbital becomes clear from the
slight decrease of the bond length for X → B̃ ionization in N2 .
2
these σ resonances played a certain role in core electron spectroscopy as it was claimed
that their position would be connected with the bond length [See e.g. J. Stöhr, NEXAFS
Spectroscopy, Vol. 25 of Spr. Ser. Surf. Sci. (Springer, Heidelberg, 1992)]. According
to the findings of B. Kempgens, H. M. Köppe, A. Kivimäki, M. Neeb, K. Maier, U.
Hergenhahn, and A. M. Bradshaw [Phys. Rev. Lett. 79, 35 (1997)] this statement is not
so easily verified as that what can be seen as the maximum in most NEXAFS resonances
is not the σ resonance but a mixture of this resonance with some shake up structures.
22
Table 3.1: Equilibrium bond distances and vibrational frequencies of N2 and
O2 and the lowest states some of their ions.
orbital occupation
molecule term Te /eV re /Å ωe /cm−1 2σu 1πu 3σg 1πg
0.0 1.094
2369
2
4
2
0
N2
X 1 Σ+
g
+
2 +
N2
X̃ Σg
15.6 1.116
2207
2
4
1
0
+
2
N2
à Πu
16.7 1.174
1903
2
3
2
0
+
2 +
N2
B̃ Σu
18.8 1.075
2420
1
4
2
0
O2
X 3 Σ−
0.0
1.207
1580
2
4
2
2
g
+
2
O2
X̃ Πg
12.1 1.123
1876
2
4
2
1
+
4
O2
ã Πg
16.0 1.381
1035
2
3
2
2
+
4 −
b̃ Σg
19.0 1.280
1196
2
3
2
2
O2
Alternatively, also the vibrational frequencies allow to state about the
strength of the bond. Strong bonds give rise to high vibrational frequencies
and vice versa.
3.2
Is there a chemical bond in He2?
It is simple to answer the title question if one has in mind what we have
learned about bonding and antibonding orbitals in the H+
2 molecule. Applying this straightforwardly without worrying about the additional electrons
in the system,3 we obtain a picture like that shown in Figure ??. As we
have to fill four electrons in this system, we can easily see that there is no
chemical bond in He2 . The energy of the molecule is higher than the energy
of separated Helium atoms.4
This repulsion effect is called “Pauli repulsion” in order to emphasize
the connection to the Pauli exclusion principle that is the actual reason for
its existence. It is another important consequence of the resonance nature
3
In chapter 2 we have seen that the main aspects of chemical bonding are still the same
if other electrons are around, i.e. chemical bonding is a one electron property
4
In fact there is a very weak bonding mechanism that is working in He2 . This is a Van
der Waals bonding which is mainly due to the fact that the electrons on one He atom may
incidentally be both at one side of the atom. Then they have a temporal dipole moment,
that generates an electrostatic field at the other atom and induces there a dipole moment,
which has a bonding effect. It should be emphasized that the magnitude of this bonding
effect is substantially smaller than that of the chemical bond. In He2 it amounts to just a
few Kelvin (11605 K = 1 eV).
23
Table 3.2: dependence of the equilibrium bond distance of diatomic orbitals
with the valence occupation (3σ 2 4σ 4 5σ 2 1π 4 ) on the charge (Z) of the contributing atoms.
molecule
re (Å)
N2 (1 Σ+
)
1.098
g
+ 1 +
NO ( Σ ) 1.063
1 +
O2+
0.998
2 ( Σg )
of chemical bonding that we have discussed in chapter 1.1. Although it is
an antibonding effect, one should not underestimate its importance on the
nature of matter as the repulsion forces are equally important for this as the
bonding forces.
3.3
Bond length dependence on Z
One effect of Pauli repulsion, but maybe not the most obvious one is that
there exists a dependence of bond lengths on the charge of the the atom. The
increase of this charge causes that the orbitals are stronger attracted but the
atom and that their sizes shrink. Therefore, also Pauli repulsion starts only at
a smaller bond distance and the same applies to the shielding of the positive
charges of the nuclei. One can see this on the ζ dependence of the ground
state energy of H+
2 [Eq. (1.13)] that becomes clear from Eqs. (1.15–1.28).
This effect causes that bond distances of molecules with equal valence
occupation but increasing nuclear charge decrease. In Tab. 3.2 this is shown
5
for the isovalence electronic systems N2, NO+ and O2+
2 . This clearly indicates that the dependence discussed above is working very effectively in these
molecules.
It should be stated that O2+
is in several respects an unique molecule. In fact the
2
bond length in Table 3.2 does not represent the minimum of the O+ – O+ potential energy
curve, but this minimum is located at infinite separation. Nevertheless, the molecule is
well observable in the gas phase as the potential energy curve shows a very pronounced
minimum at 0.998 Å bond length but also another maximum at longer bond distances.
The tunnelling life time of the vibrational ground state of O2 (for dissociation in two O+
fragments) is several million years.
5
24
Table 3.3: Equilibrium bond lengths of iso valence electronic and neutral
molecules.
molecule
N2
CO
BF
3.4
re (Å)
1.098
1.128
1.262
Heteronuclear molecules
For heteronuclear molecules, basically the same bonding properties apply as
for the homonuclear ones. The main change is that the gerade and underade
symmetries are no more appropriate for their naming and, therefore, the
orbitals in Fig. 3.1 should be called 1σ, 2σ, 3σ, 4σ, 1π, 5σ, 2π, and 6σ instead
of 1σg , 1σu , 2σg , 2σu , 1πu , 3σg , 1πg , and 3σu . But the bonding, nonbonding,
and antibonding characters of these orbitals mostly stay the same if the
difference in electronegativity of the two bond partners is not too big. The
latter case applies to the extreme case of ionic molecules like LiF, NaCl, etc.
For them another type of bond starts to dominate the interaction. This is
the so called ionic bond that is simply described by the fact that one electron
is transferred from the less electronegative atom to the more electronegative
one. For sodium fluoride this would correspond to the form
Na+
F− .
(3.1)
Interestingly, also for this case the resonance effect of the chemical bond
plays an important role for the bonding mechanism, but ironically just in the
opposite way than for the chemical bond. Here it is a completely classical
effect (the Coulomb attraction of the positively and negatively charged ions)
that causes the bonding. The resonance effect – the Pauli repulsion between
the fully occupied Na+ (1s2 2s2 2p3 ) and the F− (1s2 2s2 2p3 ) orbitals — is also
operative, but it limits the distance between the atoms to the sum of the
orbital radii.
So in the ionic bonding mechanism an overlap between the orbitals of the
two fragments is not allowed, whereas it is necessary for chemical bonding. So
ionic bonds are longer than comparable chemical bonds. This is already true
if one goes from a homonuclear molecule to an isovalent electronic heteronuclear species with increased electronegativity difference between the bond
partners. Table 3.3 shows this effect. It seems that the bond length increase
is an effect that depends roughly on the square of the charge difference.
25
Note that heteronuclear chemical bonds between atoms with very different
electronegativity become more and more ionic, which in turn lengthens the
bonds.
3.5
π 2 configurations
In the context of linear molecules one frequently encounters the case that a
doubly degenerate π orbital, in which up to four electrons may be filled in,
is occupied only with two electrons. This is for example the case in the O2
molecule, whose importance is out of question even for people who consider
all this scientific business with atoms and small molecules as obsolete and
out of fashion. It is a bit involved to understand the terms that arise from
this electronic configurations. Thus, some intendedly qualitative arguments
on the electronic structure will be given in this section.
If we consider this system with the Cartesian π orbitals πx and πy , then
the following determinants may be formed
Φ1 = |πx πy |
Φ2 = |π̄x πy |
Φ3 = |πx π̄y |
Φ4 = |π̄x π̄y |
Φ5 = |πx π̄x |
Φ6 = |πy π̄y |
MS
MS
MS
MS
MS
MS
=1
=0
=0
= −1
=0
= 0.
(3.2)
(3.3)
(3.4)
(3.5)
(3.6)
(3.7)
In these equations we have used, as before, overbars in order to designate β
spin orbitals. From the MS values of these determinants it is quickly clear
that the MS = 1 and MS = −1 configurations must correspond to a Triplet
state. The corresponding MS = 0 triplet state6 can be easily generated by
applying the spin step down operator
Ŝ− =
X
i
0 0
1 0
!
(i).
(3.8)
√
to |πx πy |. The result is 1/ 2(|π̄x πy | + |πx π̄y |). Being sloppy we can say that
we apply the spin down operator first on the πx and then on the πy spin
orbital in the determinant |πx πy |. In exercise 6 this configuration will be
6
Recall, that any triplet state consists of three components with MS = −1, 0, and 1, or
more generally any 2S + 1 state has 2S + 1 components (that’s where the names of these
things stem from) with MS = −S, −S + 1, . . ., S.
26
considered in more detail. Then it will become clear that the Λ quantum
number7 of the configuration is 0. I.e. it corresponds to a 3 Σ state.
Now two different types of Σ sates exist which can be differentiated according to the symmetry behaviour of the wave function with respect to any
mirror plane that contains the bonding axis. We choose the bond axis as
conventionally to be the z axis and we investigate Φ1 with respect to the
arbitrarily chosen mirror plane σ̂xz . It is easy to see that
σ̂xz πx = πx
(3.9)
σ̂xz πy = −πy .
(3.10)
σ̂xz |πx πy | = |πx (−πy )| = −|πx πy |
(3.11)
and
Therefore,
and the |πx πy | configuration has the symmetry 3 Σ− .
Now we may wonder what the other minus linear combination of the
determinants occuring the MS = 0 component of the 3 Σ− state corresponds
to. It will turn out that this has a 1 ∆ symmetry and the other component
of this is the configuration
1
√ (|πx π̂x | − |πy π̂y |) ,
2
(3.12)
for which is it straightforward to see that it must be a singlet, as it contains
two electrons in either the πx or the πy orbitals. Again we could wonder what
happens with the plus linear combination of the latter two determinants.
This can be shown to have 1 Σ+ symmetry.
3.6
Exercise
5. The Z+1 approximation implies that for removal of a core electron
the valence electrons will suddenly be in a nuclear potential which is
less shielded by the electrons closest to the nucleus. The potential
changes to that which would be similar to adding one more charge to
the nucleus, hence the name Z+1 approximation. Thus a core ionized
nitrogen atom would have energy levels similar to oxygen if we ionized
one electron from the outermost shell in oxygen to make the valence
orbital occupation the same. For a molecule the analogy is exact. The
7
Λ is the projection of the total angular momentum of the electronic wave function on
the bond axis.
27
core ionized nitrogen molecule, N2 , is then equivalent to NO with the
outermost valence electron ionized.
The bond lengths of the ground state CO molecule and its 1s−1 2π 1
excited and 1s−1 ionised states are given in the table below:
state
term
CO
X 1 Σ+
2
CO (C 1s−1 2π 1 )
Π
−1
1
2
CO (O 1s 2π )
Π
−1
2 +
CO (C 1s )
Σ
−1
2 +
CO (O 1s )
Σ
re [Å]
1.128
1.153
1.291
≈ 1.063
≈ 1.153
Discuss the trends of these bond length dependences with the Z + 1
or equivalent core approximation, which says that an atom with a
core hole behaves chemically like the atom with a nuclear charge increased by one. For CO core ionized carbon is replaced by nitrogen, and
core-ionized oxygen is replaced by fluorine. The two ”core-equivalent”
molecules are thus NO and CF.
The parameters regarding the ground and ionized states in these two
systems are given in the table:
state
NO neutral ground state
NO ionic ground state
CF neutral ground state
CF ionic ground state
re [Å] term
1.151 X 2 Π
1.063 X 1 Σ
2
1.272
Π
1 +
1.154
Σ
6. The possible symmetries of a π 2 configuration and their representation in configuration state functions (CSFs)8 (including all degenerate
representations) are
3
Σ− : |πx πy |; √12 (|πx π̄y | + |π̄x πy |); |π̄x π̄y |
1
1
∆ :
Σ+ :
1
√
2
(|πx π̄y | − |π̄x πy |); √12 (|πx π̄x | − |πy π̄y |)
√1
2
(|πx π̄x | + |πy π̄y |)
8
A configuration state function is a linear combination of Slater determinants which
all have the same occupation of orbitals. The linear combination is made such that spin
and spatial symmetry requirements are fulfilled
28
transform these CSFs in the basis of the complex π± orbitals
π+ =
π− =
(−πx − iπy )
√1 (πx − iπy )
2
1
√
2
which have well defined λ quantum numbers (±1). One transformation
for each symmetry is sufficient. Use |ϕψ| = −|ψϕ| and again |ψψ| = 0!
What can you say about the Λ quantum numbers of the CSFs?
29
B – Electronic structure
and
Symmetries
(Diatomic &Polyatomic molecules)
Chapter 1
Brief introduction to molecular
symmetry
It is possible to understand the electronic structure of diatomic molecules
and their interaction with light without the theory of molecular symmetry.
But understanding molecular symmetry is essential, e.g., for the treatment
of selection rules in polyatomic molecules. In this course, we only present the
most basic elements of molecular symmetry, and we do it in a largely nonmathematical way. See Chapter 5 in Molecular Quantum Mechanics (Atkins
and Friedman) for more details of the underlying mathematical theory: group
theory.
1.1
Symmetry operations and elements
A symmetry operation is an operation that leaves an object apparently
unchanged. For example, a rotation of a sphere through any angle around
its center is a symmetry operation. Every object has at least one symmetry
operation: the identity, the operation of doing nothing. To each symmetry
operation there corresponds a symmetry element, the point, line or plane
with respect to which the operation is carried out. In order to discuss the
symmetry of molecules, we need five symmetry elements.
I or E The identity operation, the act of doing nothing. The corresponding
symmetry element is the object itself.
Cn An n-fold rotation, a rotation by 2π/n around an axis of symmetry.
0
Figure 1.1: Examples of the Cn axes of rotation.
If an object has several axes of rotation, the one with the largest value
of n is called the principal axis. In this course, we assume that the
rotations are performed clockwise, when viewed from above.
σ A reflection in a mirror plane. When the mirror plane includes the
the principal axis of symmetry, it is called a vertical plane and denoted
σv . If the principal axis is perpendicular to the mirror plane, the latter
symmetry element is called a horizontal plane (σh ). A dihedral plane
(σd ) is a vertical plane that bisects the angle between two C2 axes that
lie perpendicular to the principal axis.
i An inversion through a centre of symmetry.
Sn An improper rotation through an axis of improper rotation. An
improper rotation is a composite operation, where an n-fold rotation is
followed by a reflection in a plane that is perpendicular to the n-fold
axis. Neither operation alone is in general a symmetry operation, but
the overall outcome is.
1
Figure 1.2: Symmetry elements of the (a) H2 O and (b) BF3 molecules.
1.2
The classification of molecules
To classify a molecule according to its symmetry, we list all of its symmetry
operations, and then ascribe a label, the point group to the molecule based
on the list of those operations. The term ’point’ indicates that after performing all the operations of the point group, at least one point of the molecule
does not move at all. For the notation we use the Schoenflies system, where
the name of the point group is based on a dominant feature of the symmetry
of the molecule.
The point groups are:
1. The groups C1 , Cs and Ci . These groups consist of the identity alone
(C1 ), the identity and reflection (Cs ), and the identity and an inversion
(Ci ).
2. The groups Cn . These groups consist of the identity and an n-fold
rotation.
3. The groups Cnv In addition to the operations of the groups Cn , these
groups also contain n vertical reflections. An important example is
the group C∞v , the group to which heteronuclear diatomic molecules
belong.
4. The groups Cnh . In addition to the operations of the groups Cn , these
groups also contain a horizontal reflection (together with whatever operations the presence of the operations implies).
2
5. The groups Dn . In addition to the operations of the groups Cn , these
groups possess n two-fold rotations perpendicular to the n-fold (principal) axis (together with whatever operations the presence of the operations implies).
6. The groups Dnh . These groups consist of operations present in Dn ,
together with a horizontal reflection (and together with whatever operations the presence of the operations implies). An important example
is the group D∞h , the group to which homonuclear diatomic molecules
belong.
7. The groups Dnd . These groups consist of operations present in Dn and
n dihedral reflections (together with whatever operations the presence
of the operations implies).
8. The groups Sn , with n even. These groups contain the identity and
an n-fold improper rotation (together with whatever operations the
presence of the operations implies).
9. The cubic (T, Th , Td , O, Oh ) and icosahedral (I, Ih ) groups. These groups
contain more than one n-fold rotation with n ≥ 3.
10. The full rotation group, R3 . The group consists of all rotations through
any angle and in any orientation. This is the symmetry group of the
sphere and atoms.
1.3
Calculus of symmetry elements
In the list above, we have indicated that the presence of certain symmetry
operations implies that some other symmetry operations automatically exist. For example, the point group C2h automatically possess an inversion,
because a rotation by 180◦ followed by a horizontal reflection is equivalent
to inversion. This can be written as an equation
σh C2 = i.
(1.1)
It is a general feature of symmetry operations that the outcome of a joint
symmetry operation is always equivalent to a single symmetry operation
RS = T,
3
(1.2)
where R, S and T all are symmetry operations of the group. The operation
S is carried out first, R after that.
We can say that σh and C2 generate the element i; they can be regarded
as generating elements. We can generate other elements from the symmetry
element Cn by raising it to the power of 1, 2, 3, . . . , (n-1). For example, if
there is an element C3 , there must be also C32 , where
C32 = C3 × C3 .
(1.3)
C32 is a rotation clockwise by 2 × (2π/3) radians. It also corresponds to a
rotation counterclockwise by (2π/3), which can labeled with a symbol C3−1 .
This is the inverse of the operation C3 . Generally
Cnn−1 = Cn−1 .
(1.4)
We can also generate the powers of Sn from the element Sn . For example,
we obtain for S4
S42 = C2
(1.5)
S43 = S4−1 ,
where S4−1 means a counterclockwise rotation by 2π/4 rad followed by a
reflection. The inverse σ −1 of the reflection is the reflection itself.
The properties of the symmetry operations in point groups fulfil the same
requirements that are necessary for a set of entities to form a group in mathematics. Consequently, the mathematical theory of groups, group theory,
may be applied to the study of the symmetry of molecules.
1.4
Character tables
Point groups are either non-degenerate or degenerate. A degenerate point
group contains a Cn axis with n > 2 or an S4 axis. A molecule belonging to
such a point group may have degenerate properties, e.g., electronic wavefunctions or vibrational wavefunctions that have the same energies. A molecule
that belongs to a non-degenerate point group cannot have degenerate properties.
We have seen how molecules can be classified into point groups according
to the locations of their nuclei in the equilibrium geometry. Molecules can,
however, have properties such as the above mentioned wave functions that
do not have all the symmetry elements of the point group. Character tables
4
are used to classify the symmetries of these properties. We will inspect the
character tables of the C2v , C3v and C∞v point groups. The first of them is
non-degenerate, the second degenerate and the third an example of a point
group with an infinite number of symmetry elements.
1.4.1
The C2v character table
For example, the vibrational wavefunction of H2 O may or may not have
a certain symmetry element. If it has the element, the application of the
corresponding symmetry operation does not affect the wavefunction, which
we can write
σv
ψv −→(+1)ψ
(1.6)
v
and say that ψv is symmetric with respect to σv . The only other possibility
in a non-degenerate point group is that the wavefunction changes sign in the
operation
σv
ψv −→(−1)ψ
(1.7)
v,
in which case ψv is antisymmetric with respect to σv . The numbers +1 and
-1 appearing in equations (1.6) and(1.7) are known as the characters of ψv
with respect to σv (in this particular case).
Any two of the elements C2 , σv (xz) and σv0 (yz) can be regarded as generating elements. There are four possible combinations of characters with
respect to these generating elements: +1 and +1, +1 and -1, -1 and +1, and
+1, -1, -1. These are listed in the third and fourth columns of the character
table below. We have selected C2 and σv (xz) as the generating elements. The
characters under I have to be always 1. Just as σv0 (yz) can be generated by
C2 and σv (xz), the characters under σv0 (yz) are the products of the characters
under C2 and σv (xz). Each of the four rows of the characters is called an
irreducible representation of the group and are labeled for practicality with
the symmetry species A1 , A2 , B1 and B2 . The A1 is said to be totally
symmetric because all of its characters are +1. The three other species are
non-totally symmetric.
The notation of the symmetry species follows the convention. A indicates
the symmetry with respect to C2 , B antisymmetry. The subscripts indicate
symmetry (1) and antisymmetry (2) with respect to σv (xz).
In the sixth column of the character table, the symmetry species are given
for the translations (T ) of the molecule along the coordinate axes and for the
rotations (R) around the axes. In Fig. 1.4 the vectors attached to the nuclei
5
Table
C2v
A1
A2
B1
B2
1.1: The character table
I C2 σv (xz) σv0 (yz)
1 1
1
1
1 1
-1
-1
1 -1
1
-1
1 -1
-1
1
of the C2v point group.
Tz
Rz
Tx , Ry
Ty , Rx
αxx , αyy , αzz
αxy
αxz
αyz
of the H2 O molecule represent these displacements, which have the symmetry
species according to how they behave under the operations C2 and σv (xz).
Figures 1.4(a) and (b) show that
Γ(Tx ) = B1 ; Γ(Ty ) = B2 ; Γ(Tz ) = A1
(1.8)
Γ(Rx ) = B2 ; Γ(Ry ) = B1 ; Γ(Rz ) = A2 .
(1.9)
The symbol Γ stands generally for a representation. In this case it is an
irreducible representation of the symmetry species. The symmetry species
of the translations are needed, when selection rules of electronic transitions
are determined for polyatomic molecules. The symmetry species for the
components of the symmetric polarizability tensor α, given in the last column
of the character table, are needed in Raman spectroscopy.
Let us look at an N -atomic molecule. 3N coordinates are needed to
specify its location accurately, i.e. three Cartesian coordinates for each atom.
Each atom may change its location by varying one of its three coordinates, so
the total number of displacements available is 3N . We say that the molecule
has 3N degrees of freedom. These can be arranged in a physically sensible
way. Three coordinates are needed to specify the location of the centre of
mass along the coordinate axes (translational degrees of freedom). Furthermore, three coordinates are needed to specify the orientation of the molecule
with respect a coordinate system that is fixed in space. The movement about
these coordinates corresponds to the rotational motion of the molecule (rotational degrees of freedom). The remaining 3N − 6 coordinates represent
the movements of the nuclei with respect to each other, that is vibrations
(vibrational degrees of freedom). Linear molecules have, however, 3N − 5
vibrational degrees of freedom, because the moment of inertia about the
molecular axis is zero and the corresponding rotational motion has no degree
of freedom.
6
Figure 1.3: The (a) translations and (b) rotations of the H2 O molecule.
The molecule has the same number of normal modes (of vibration) as
it has vibrational degrees of freedom. A normal mode means an idealized
vibrational motion where all the nuclei move harmonically with the same
frequency and phase, but generally with different amplitudes. Every normal
mode has its characteristic frequency. Every vibrational motion of a molecule
can be represented as a sum of normal modes.
The H2 O molecule has thus three normal modes, which are shown in Fig.
1.5. The arrows fixed to the nuclei indicate the directions and amplitudes
of the displacements. The symmetry species of each vibration can be determined using the C2v character table. We obtain the following characters
under the operations C2 and σv (xz): +1 and +1 for ν1 , +1 and +1 for ν2 ,
and -1 and -1 for ν3 . Therefore
Γ(ψν(1) ) = A1 ; Γ(ψν(2) ) = A1 ; Γ(ψν(3) ) = B2 .
(1.10)
The classification of molecular properties into the symmetry species depends on the choice of the axes. The convention for a planar molecule of
C2v symmetry is that the z axis is parallel to the C2 axis and the x axis is
perpendicular to the molecule. We follow this convention. If we interchanged
x and y axes, then Γ(ψv(3) ) would be B1 , not B2 . It is important to mark
the axes chosen on the picture.
7
Figure 1.4: The normal modes of the H2 O molecule.
Figure 1.5: The normal modes of formaldehyde.
Example 1.1. Formaldehyde is a planar molecule and it has six normal modes
that can be roughly illustrated as in the figure below. Determine the symmetry
species of the normal modes in the proper point group using the axes drawn on
the picture.
Solution. Formaldehyde belongs to the C2v point group. Using the C2v character
table, the characters of the vibrations can be classified as shown on the following
page.
It follows from these that symmetry species Γ(ψv ) of the vibrations are:
Γ(ψv(i) )
Γ(ψv(ii) )
Γ(ψv(iii) )
Γ(ψv(iv) )
Γ(ψv(v) )
Γ(ψv(vi) )
=
=
=
=
=
=
A1
B2
A1
B2
A1
A2
The classification can be done using any two of the symmetry elements C2 ,
8
Table 1.2: The characters of
Vibration I
(i)
1
(ii)
1
(iii)
1
(iv)
1
(v)
1
(vi)
1
the normal modes of formaldehyde.
C2 σv (xz) σv0 (yz)
1
1
1
-1
-1
1
1
1
1
-1
-1
1
1
1
1
-1
1
-1
σv (xz) and σv0 (yz), because they generate the third one and the character under
E is always 1 in this point group.
These vibrations can be described with terms: (i) symmetric CH stretch, (ii)
antisymmetric CH stretch, (iii) CH2 scissors, (iv) CH2 rocking, (v) CO stretch and
(vi) out-of-plane bending.
Often we have to multiply symmetry species, or as expressed in the language of group theory, form their direct product. For example, if one quantum is excited in both the ν1 and ν3 modes, the symmetry species of the
wavefunction of this state is
Γ(ψv ) = A1 × B2 = B2 .
(1.11)
In order to form the direct product of two symmetry species we multiply the
characters under each symmetry element using the rules
(+1) × (+1) = 1; (+1) × (+1) = −1; (−1) × (−1) = 1.
(1.12)
The result of Eq. (1.11) has been obtained in this way. If two ν3 quanta are
excited in H2 O
Γ(ψv ) = B2 × B2 = A1 .
(1.13)
The results of multiplications in Eqs. (1.11) and (1.13) generally apply to
non-degenerate point groups. Thus (a) the product of any symmetry species
with a totally symmetric species does not change the symmetry species and
(b) the product of any symmetry species with itself gives a totally symmetric
species.
It can also be shown that in the C2v point group
A2 × B1 = B2 ; A2 × B2 = B1 .
9
(1.14)
C3v
A1
A2
E
Table 1.3: The C3v character table.
I 2C3 3σv
1
1
1 Tz
αxx + αyy , αzz
1
1
-1 Rz
2
-1
0 (Tx , Ty ), (Rx , Ry ) (αxx − αyy , αxy ), (αxz , αyz )
Figure 1.6: In the C3v point group the elements C3 and C32 belong to the
same class.
1.4.2
The C3v character table
The character table of the C3v is given above. There are two obvious differences from the character tables of any non-degenerate point groups. Firstly,
the elements of the same class are grouped together, namely C3 and C32 →
2C3 , and σv , σv0 and σv00 → 3σv .
Two elements P and Q belong to the same class, if there is a third element
so that
P = R−1 × Q × R.
(1.15)
From Fig. 1.6 we see that in the C3v point group
C3 = σv−1 × C32 × σv
(1.16)
and therefore C3 and C32 belong to the same class. The symmetry elements
belonging to the same class have the same characters. The number of the
symmetry species is equal to the number of the classes. This also applies to
non-degenerate point groups, where each element forms its own class.
The other difference in the character table is the appearance of the doubly
degenerate symmetry species E. Its characters are not always +1 or -1, in
contrast to those in non-degenerate point groups.
10
Figure 1.7: The normal modes of the NH3 molecule.
The characters of the symmetry species A1 and A2 have the same meaning
as in the non-degenerate point group. The characters of the symmetry species
E can be understood from the example of the normal modes of the NH3
molecule, shown in Fig. 1.7. The vibrations ν1 and ν2 are clearly of the species
a1 (A recommendation: small letters are used for the symmetry species of
the vibrations and electron orbitals, whereas capital letters are used for the
symmetry species of the corresponding wavefunctions.) The vibrations ν3a
and ν3b are degenerate; it requires the same amount of energy to excite one
quantum in either of them, but they clearly have different wavefunctions.
Similarly, ν4a and ν4b are degenerate.
Normal coordinates are such a set of coordinates for a coupled system that
the equations of motion only contain one of these coordinates. The symmetry
properties of the vibrational wavefunction ψv are identical to those of the
corresponding normal coordinate. If in the C3v point group the C3 operation
is applied to Q1 , which is the normal coordinate of the ν1 vibration, it changes
to Q01 , where
C3
Q1 −→
Q01 = (+1)Q1 .
(1.17)
If the symmetry operation is applied to a degenerate normal coordinate, it
11
doesn’t simply remain the same or change its sign, but generally changes
to a linear combination of two degenerate normal coordinates. Thus when
applying a symmetry operation S
S
Q3a −→ Q03a = daa Q3a + dab Q3b
S
Q3b −→ Q03b = daa Q3a + dab Q3b .
(1.18)
This can be written with the help of matrices
Q03a
Q03b
=
daa
dba
dab
dbb
Q3a
Q3b
(1.19)
The relation daa + dbb is called the trace of the matrix, and it is the character
of the property (in this case of the normal coordinate) with respect to the
symmetry operation S.
The character of the symmetry species E with respect to the identity I
can be obtained from the relations
I
Q3a −→ Q03a = 1 × Q3a + 0 × Q3b
I
Q3b −→ Q03b = 0 × Q3a + 1 × Q3b
or
(1.20)
1 0
Q03a
Q3a
=
(1.21)
0
Q3b
0 1
Q3b
The trace of the matrix is 2, which is the character of the symmetry species
E under I.
One of the two ν3 vibrations, ν3a , is symmetric in reflection through that
σv plane, which bisects the angle between H1 and H2 , and the other vibration
is antisymmetric. We obtain
Q03a
Q03b
=
1 0
0 −1
Q3a
Q3b
(1.22)
Therefore the character of E under σv is 0. Because all the mirror planes are
equivalent, the character must be the same also under σv0 and σv00 .
When the operation is a rotation by the angle φ around the Cn axis (in
this case φ = 2π/3 rad), the transformation of the coordinates becomes
Q03a
Q03b
cos φ sin φ
Q3a
=
−
sin
φ
cos
φ
Q3b
q 

3
1
−
2  Q3a
=  q2 3
Q3b
− 2 − 12
12
(1.23)
The trace of the matrix is -1, which is also the character of the symmetry
species E under C3 .
Apart from E × E, direct products are formed using the same rules as in
non-degenerate point groups: the characters of the product are obtained by
multiplying the characters of the symmetry species. We get
A1 × A2 = A2 ; A2 × A2 = A1 ; A1 × E = E; A2 × E = E.
(1.24)
In the product E × E we again use the normal modes of the NH3 molecule as
an example. The result depends on whether we need a representation Γ(ψv ),
when (a) one quantum of each vibration is excited or (b) when two quanta
of the same vibration are excited (= overtone). In the case (a), for example
for the combination ν3 + ν4 , the product is written E × E and the result is
obtained by squaring the characters with respect to each operation
I 2C3 3σv
E×E 4 1
0
(1.25)
The characters 4, 1 and 0 span a reducible representation in the C3v point
group. We have to reduce it to a set of irreducible representations, whose
sum of the characters is the same as in the reducible representation. This
can be expressed as an equation
χC (k) × χD (k) = χF (k) + χG (k) + . . .
(1.26)
where χ is the character of whatever operation k and the multiplication of
the degenerate symmetry species C and D gives the result
C × D = F + G + ...
(1.27)
The reduction of the representation E×E yields a unique set of irreducible
representations, which is
E × E = A1 + A2 + E.
(1.28)
We can see from Table 1.3 that the sum of the characters of A1 , A2 and E
under I, C3 and σv gives the irreducible representation of equation (1.25).
In the case (b), when two quanta of the same vibration are excited (e.g.,
2ν3 ), the product is written (E)2 , where
(E)2 = A1 + E.
13
(1.29)
C∞v
A1 ≡ Σ+
A2 ≡ Σ−
E1 ≡ Π
E2 ≡ ∆
E3 ≡ Φ
..
.
I
1
1
2
2
2
..
.
Table 1.4: T heC∞v character table.
φ
2C∞
. . . ∞σv
1
...
1 Tz
αxx + αyy , αzz
1
...
-1 Rz
2 cos φ . . .
0 (Tx , Ty ), (Rx , Ry ) (αxz , αyz )
2 cos 2φ . . .
0
(αxx − αyy , αxy )
2 cos 3φ . . .
0
..
..
.
...
.
This is called the symmetric part of E × E; it is symmetric to the particle
interchange. The result of Eq. (1.29) is obtained by forming first the product
E × E. One part of the product is forbidden. In a degenerate point group
it is an A symmetry species, and if possible a non-totally symmetric. In
the present case, the symmetry species A2 is forbidden and it forms the
antisymmetric part of the product E × E.
There are tables that give the symmetry species for all degenerate combined vibrations in all degenerate point groups (See Appendix 1 in MQM).
1.4.3
The C∞v character table
The C∞v point group has an infinite number of classes, since the rotation
around the C∞ axis can be performed by whatever angle φ and each of the
−φ
φ
, a counterclockwise
belongs to a different class. However, C∞
elements C∞
φ
rotation by φ belongs to the same class as C∞ . Because the number of
classes is infinite, so is also the number of symmetry species. Their labels are
A1 , A2 , E1 , E2 , . . . E∞ , if we follow the convention used in other character
tables. Unfortunately, another practice had been taken into use particularly
in electron spectroscopy of diatomic molecules before the notations for the
symmetry species had been widely accepted. The electronic states were given
symbols Σ, Π, ∆, Φ, . . . corresponding to the orbital angular momentum
quantum number Λ that can have values 0, 1, 2, 3, . . . (we will tell more
about Λ later). These latter symbols are predominantly used in the C∞v and
D∞h point groups. Both the systems are shown in the C∞v character table
above.
The multiplication of the symmetry species is performed following the
14
usual rules. Thus, for example
Σ+ × Σ− = Σ− ;
Σ− × Π = Π;
Σ+ × ∆ = ∆.
(1.30)
The reducible representation of the product Π × Π is
I
Π×Π 4
φ
2C∞
∞σv
2
4 cos φ
0
(= 2 + 2 cos 2φ)
(1.31)
which is reduced as follows
Π × Π = Σ+ + Σ− + ∆.
(1.32)
The same rule that was used to obtain (E)2 from E × E in the C3v point
group gives
(Π)2 = Σ+ + ∆.
(1.33)
Example 1.2. List the symmetry elements of the following molecules: (a) 1,2,3trifluoro benzene, (b) 1,2,4-trifluoro benzene, (c) 1,3,5-trifluoro benzene, (d) 1,2,4,5tetrafluoro benzene, (e) hexafluoro benzene, (f) 1,4-dibromo-2,5-difluoro benzene.
A molecule has a permanent dipole moment if one or more of the symmetry
species of the translations Tx , Ty and Tz is totally symmetric. Apply this principle
for each molecule by using a relevant character table and draw the directions of
the dipole moments, if it 6= 0.
Solution. The picture on the next page
(a) In the C2v point group, Γ(Tz ) = A1 (see table 1.1). Thus a permanent dipole
moment exists and its direction is along the C2 axis. Because of the large electronegativity of fluorine, the negative end δ− of the dipole is towards the fluorine
atoms and the positive end δ+ towards the hydrogen atoms.
(b) In the Cs point group, Γ(Tx , Ty ) = A0 (totally symmetric). The dipole moment
is therefore on the xy plane. Symmetry doesn’t determine for it to be in any specific
direction in this plane. As compared to 1,2,3-trifluoro benzene, the transfer of a
fluorine atom from the place 3 to place 4 deviates the dipole moment towards the
place 4.
(c)-(f) These molecules don’t have permanent dipole moments, confirmed by the
relevant character tables.
15
16
Chapter 2
Electronic structure of simple
molecules
2.1
Hydrogen molecule
The electron configuration of the H2 molecule in the ground state is 1σ 2 .
Both electrons are in the lowest orbital, and the spatial wave function remains the same if the electrons are interchanged, i.e. it is symmetrical. In
order that the total wavefunction is antisymmetric, the spin component
must √
be antisymmetric to the particle interchange. The spin contribution
is (1/ 2){α(1)β(2) − α(2)β(1)}, where α and β signify the spin-up and spindown states. The two electrons enter the molecular orbital with paired spins
(↑, ↓).
The term symbol of the H2 molecule in the ground state is 1 Σ+
g . The
notation system bears a close resemblance to that used for atoms (2S+1 LJ ).
The superscript 1 is the multiplicity of the state. In the present case, the total
spin quantum number S = 0, as the spins are paired. The Σ (S for atoms)
indicates that the total orbital angular momentum around the internuclear
axis (z) is zero because both electrons occupy σ-orbitals. More formally, the
component of orbital angular momentum about the axis can have possible
values Lz = λh̄, where λ = 0, ±1, ±2, . . . . The following letters are used to
indicate the | λ | value:
|λ| 0 1 2 3 ···
Letter σ π δ φ · · ·
(2.1)
We denote the total orbital angular momentum around the internuclear
17
axis as Λ:
Λ=
X
λi ,
(2.2)
i=1
where λi is the orbital angular momentum about the axis for each electron.
Now λ1 = λ2 = 0, so Λ = 0. For Λ we use capital Greek letters Σ, Π, ∆, Φ
. . . corresponding to the values 0, 1, 2, 3 . . . , respectively, of |Λ|. Thus for
the ground state of H2 we obtain a Σ term.
The subscript g indicates that the overall parity of the state is g. To
calculate it from the individual values for each electron, we use
g×g =g
2.2
g × u = u u × u = g.
(2.3)
Homonuclear diatomic molecules
The molecular orbitals for diatomic molecules that are larger than H2 can be
constructed in the same way by using linear combinations of atomic orbitals
(LCAO)
X
ψ=
cr φr .
(2.4)
r
Effective combinations are obtained when the following conditions are fulfilled:
1. The energies of the atomic orbitals are similar.
2. The atomic orbitals overlap each other as much as possible.
3. The atomic orbitals have the same symmetry with respect to rotations
about the internuclear axis.
We form linear combinations of only those atomic orbitals that have the
same symmetry species in the molecular point group. In homonuclear diatomic molecules, the atomic orbitals of identical energy dominate the bonding. The strongest bonds will therefore have combinations such as (2s, 2s)
and (2p, 2p), and there is no need (for qualitative discussions, at least) to
consider (2s, 1s) and (2p, 1s) contributions. There is normally insufficient
energy difference between 2s- and 2p-orbitals to ignore safely (2s, 2p) contributions, even though in simple diagrams (like in Figure 2.2(a)) this is often
done.
18
Let us set up a plausible energy level diagram for the molecular orbitals of
the Period 2 homonuclear diatomic molecules. We consider only the valence
orbitals. From atomic orbitals of Σ symmetry (2s and 2pz of each atom)
we can form four linear combinations. In the first approximation, we can
think of 2s-orbitals forming bonding and antibonding combinations and the
2pz orbitals doing the same. However, it’s better to think of four combinations emerging from the four atomic orbitals. They all have mixed 2s and
2pz character, with the lowest energy combination (2σg ) predominantly 2s
orbital in character and the highest energy combination (3σu ) predominantly
2pz orbital in character. The four orbitals of Π symmetry (atomic 2px and
2py orbitals) likewise form four combinations, but they fall into two doubly
degenerate sets, which we call 1πu and 1πg . It is hard to predict the relative
ordering of the σ and π sets. Indeed, the energy order of the 1πu and 3σg
orbitals in N2 is interchanged when going to O2 and F2 .
The terms HOMO and LUMO are used to refer to the highest occupied
and lowest unoccupied orbitals, respectively. The HOMO and LUMO are
referred jointly as the frontier orbitals: the frontier is the site of much of the
reactive and spectroscopic activity of the species.
To arrive at the electron configuration of a neutral molecule, we add the
appropriate number of electrons to each orbital starting from the levels of
the lowest energy. If more than one orbital is available (π-orbitals), then
electrons first occupy separate orbitals to minimize electron-electron repulsions; moreover they do so with parallel spins. The electron configuration of
the N2 molecule in the ground state is
N2
1σg2 1σu2 2σg2 2σu2 1πu4 3σg2 .
(2.5)
All the orbitals are full in N2 , and the electrons in them contribute to give
S = 0 and Λ = 0. Hence the ground state of N2 has a term symbol 1 Σg
(more precisely, 1 Σ+
g ).
The electron configuration of the O2 molecule is
O2
1σg2 1σu2 2σg2 2σu2 3σg2 1πu4 1πg2 .
(2.6)
Because only two electrons occupy the (antibonding) 1πg orbital, they will
be in separate orbitals and have parallel spins. Hence the ground state is
predicted to be a triplet (S = 1). This is consistent with the paramagnetic
chracter of oxygen gas. To determine the value of Λ, the total orbital angular
momentum around the internuclear axis, we add together all individual λs.
19
Figure 2.1: Simple (a) and more accurate (b) molecular orbital energy level
diagrams of diatomic molecules.
For each electron in a σ-orbital, λ = 0. For π-orbitals, λ = ±1 because
each orbital corresponds to a different sense of rotation about the axis. A
π 4 configuration necessarily contributes 0 to Λ. A π 2 configuration, however,
can contribute 0 or ±2 because the two electrons can be in different orbitals
or the same orbital, respectively. Hence the configuration can give rise to a
Σ and a ∆ term, respectively. Because we expect the electrons to occupy
different orbitals, the ground state term is Σ, ∆ being higher in energy.
Moreover, because the electrons are in different different π-orbitals, they can
have either S = 0 or S = 1, so we expect 1 Σ and 3 Σ terms, with the latter
lower in energy. On the other hand, the ∆ term must have paired spins
because both the electrons occupy the same π-orbital, so giving a 1 ∆ term.
The term symbols given above for O2 are still incomplete. Terms designated Σ also require an additional right superscript of – or + to indicate the
symmetry properties of the occupied orbitals under reflection in a plane that
contains the internuclear axis. The full term symbol for the ground state of
the O2 molecule is 3 Σ−
g.
20
Figure 2.2: The experimentally determined molecular potential energy curves
of some of the lower energy states of O2 .
Exercise 2.1. Use the D∞h character table and the rules of forming the direct
products to determine which terms arise from the electronic configuration of O2
given in Eq. (2.6). Only electrons in open shells need to be considered. Coupling
of the spins has to be done separately.
The strength of the bond formed can be assessed by calculating the bond
order according to the formula:
1
Bond order = [n(bonding) − n(antibonding)].
2
(2.7)
Here n(bonding) and n(antibonding) are the numbers of electrons in bonding
and antibonding orbitals, respectively.
2.3
Heteronuclear diatomic molecules
The qualitative effect of the presence of two different atoms in a molecule is
that the electron density has a nonuniform distribution. For orbitals of the
form
ψ = cA φA + cB φB ,
(2.8)
21
Figure 2.3: The D∞h character table.
it will no longer be true that |cA |2 = |cB |2 . If A is the more electronegative atom of the two, the bonding combination will have |cA |2 > |cB |2 , and
the electron will be found predominantly on A. On the other hand, for the
antibonding combination |cA |2 < |cB |2 , and the electron will be found predominantly on B.
As the energies of the orbitals of one atom do not coincide, except by
accident, with those of the second atom, the molecular orbitals are shifted
from atomic orbitals less than for homonuclear species. This suggests that a
heteronuclear bonding system can be generated from the homonuclear system
by reducing the shifts in energy. The resulting scheme for CO is shown in
Fig. 2.4. The valence electron configuration of CO is
CO
1σ 2 2σ 2 1π 4 3σ 2 ,
(2.9)
its term symbol is 1 Σ+ . (There are two more σ orbitals corresponding to the
atomic O 1s and C 1s orbitals.) Note that the parity designation (g and u)
is no longer relevant, as the molecule lacks a centre of symmetry.
Exercise 2.2. Draw a schematic molecular orbital energy level diagram for the
NO molecule. The atomic orbital energies are: N 2p 14.5 eV, N 2s 37.3 eV, N 1s
409.9 eV, O 2p 13.6 eV, O 2s 41.6 eV, and O 1s 543.1 eV. What is the electron
configuration of NO in the ground state and what is the term symbol?
22
Figure 2.4: A schematic depiction of the molecular orbital energy levels diagram of the CO molecule.
2.4
The water molecule
The molecular orbitals of polyatomic species are linear combinations of atomic
orbitals:
X
ψ=
ci φi .
(2.10)
i
The main difference is now that the molecular orbital extends, in principle,
over all the atoms of the molecule. However, only atomic orbitals that have
the appropriate symmetry make a contribution, because only they have net
overlap with one another. Group theory can be particularly helpful in deciding which orbitals contribute to each molecular orbital, and in classifying
the resulting orbitals according to their symmetry species.
The concept behind the construction of a symmetry-adapted linear
combination (SALC) is to identify two or more equivalent atoms in a
molecule, such as the two H atoms in H2 O, and to form combinations of
the atomic orbitals they provide that belong to specific symmetry species.
Then molecular orbitals are constructed by forming linear combinations of
each SALC with an atomic orbital of the same symmetry species on the
23
central atom (O in H2 O).
Consider the water molecule, which belongs to the C2v point group. If we
take the basis (H1sA , H1sB , O2s, O2px , O2py , O2pz ) in order to construct
the MOs, we should expect a 6 × 6 determinant and a sixth order equation
to solve for energy. However, it should be clear from Fig. 2.5, that the two
linear combinations
φ(B2 ) = H1sA − H1sB
φ(A1 ) = H1sA + H1sB
(2.11)
can have net overlap with O2s and O2pz (for φ(A1 )) and with O2py (for
φ(B2 )). This suggests that MOs in H2 O will fall into following groups:
ψ(A1 ) = c1 O2s + c2 O2pz + c3 φ(A1 )
ψ(B1 ) =
O2px
ψ(B2 ) =
c4 O2py + c5 φ(B2 ).
(2.12)
When the secular determinant is constructed it will consist of three blocks,
one being three-dimensional (solution of a cubic equation for E), one being
one-dimensional (involving a trivial statement of the energy) and one being
two-dimensional (solution of a quadratic equation for E). In each case we
have identified the symmetry species of the SALC by reference to the character table and have combined it with atomic orbitals of the same symmetry
species to form a molecular orbital of this symmetry species. The molecular
orbitals (not the SALCs) are labelled by lower case letters corresponding to
the symmetry species, so in H2 O we can expect the orbitals a1 , b1 and b2 .
Each orbital of a particular symmetry is then numbered sequentially in order
of increasing energy.
The energies of the orbitals and the values of the coefficients are found by
solving the secular equation in the normal way. However, there is the added
complication that both the bond lengths and the bond angle are variable.
These parameters are varied systematically, until the total energy of the
molecule is a minimum, and that lowest energy arrangement is accepted
as the normal state of the molecule. Alternatively, if the geometry of the
molecule is known, then a single calculation may be carried out for that
arrangement of nuclei. For H2 O, the bond angle is 104◦ . The molecular
orbital energy level diagram is as shown in Fig. 2.5. As there are eight
valence electrons to accommodate, the ground-state electron configuration
of H2 O is expected to be
H2 O
1a21 1b22 2a21 1b21
24
1
A1 .
(2.13)
Figure 2.5: (a) The symmetry classification of the oxygen atomic orbitals in
H2 O, and the two symmetry-adapted linear combinations of the H1s orbitals.
(b) The molecular orbitals of H2 O at its equilibrium bond angle of 104◦ .
25
(Again there is one more a1 orbital corresponding to the atomic O1s orbital
that has not been shown in Fig, 2.5 and is not given in the electron configuration.) The overall term symbol is calculated by multiplying together
the characters of the occupied orbitals, and then identifying the symmetry
species from the character table. As all the orbitals are doubly occupied and
their characters are ±1, the result is the set (1,1,1,1), which corresponds to
A1 . All electrons are paired, so S = 0, and the multiplicity is 1.
Exercise 2.3. The lowest excited state of the water molecule can be expected to
arise from the electron configuration where one of the electrons in the HOMO has
been promoted to the LUMO. Write this electron configuration and determine the
possible term symbols.
26
C - Potential energy curves
and
Electronic transition
(Diatomic molecules)
Chapter 2
Potential energy curves and
vibrations of diatomic
molecules
2.1
Harmonic oscillator
The model of two balls connected by a spring is sufficient to describe approximatively the vibration of a diatomic molecule. The stretching and contraction of the bond is represented by the change of the length of the spring.
Hooke’s law is valid for small deviations:
Restoring force = −
dV (x)
= −kx,
dx
(2.1)
where V is potential energy, k is force constant, whose magnitude describe
the strength of the bond, and x(= r−re ) is the deviation from the equilibrium
bond length. Integration of this equation gives
1
V (x) = kx2 .
2
(2.2)
Figure 4.1 shows V (r) as a function of r. The curve is a parabola.
The Hamiltonian operator of the one-dimensional quantum mechanical
harmonic oscillator is:
h̄2 d2
1
H=−
+ kx2 ,
(2.3)
2
2µ dx
2
17
Figure 2.1: The energy levels, wavefunctions and potential energy V (r) of
the harmonic oscillator.
where µ = m1 m2 /(m1 +m1 ) is the reduced mass of the atoms. The Schrödinger
equation for the system is
2µEv µkx2
d2 ψv
+
ψv = 0.
− 2
dx2
h̄2
h̄
(2.4)
Ev = hν(v + 1/2),
(2.5)
!
It can be shown that
where ν is the classical frequency of the oscillator, which can be obtained
from
!1/2
1 k
ν=
.
(2.6)
2π µ
As expected, the frequency increases when the bond becomes stronger (when
k increases) and decreases when µ becomes larger. The vibrational quantum
number v can have values 0, 1, 2, ... .
According to Eq. (2.5) the vibrational energy levels are spaced by a constant interval of hν and the lowest energy of the oscillator (when v = 0) is
not zero but 21 hν. This zero-point energy is the lowest energy that a molecule
18
v
0
1
2
Table 2.1:
Hv (y)
1
2y
4y 2 − 2
Hermite polynomials.
v Hv (y)
3 8y 3 − 12y
4 16y 4 − 48y 2 + 12
5 32y 5 − 160y 3 + 120y
can have even at absolute temperature of 0 K. It is a result of the uncertainty
principle.
The crossing points of an energy level with the potential energy curve
correspond to the classical turning points of vibration, where the velocities
of the nuclei are zero and all energy is in the form of potential energy. In the
middle point of each energy level all energy is conversely kinetic energy.
The solutions of Eq. (2.4) are wavefunctions
ψv =
1
2v v!π 1/2
1/2
Hv (y) exp(−y 2 /2),
(2.7)
where Hv (y) is a Hermite polynomials and
y=
4π 2 νµ
h
!1/2
(r − re ).
(2.8)
Some of the Hermite polynomials are given in Table 4.1. Examples of
vibrational wavefunctions are presented in Fig. 4.1. We note the following
important properties of the wavefunctions:
1. They extend to the region outside of the parabola, which is forbidden
in a classical system.
2. When v increases those two points where the probability density ψ 2
reaches its maximum value occur close to the classical turning points.
This is illustrated in Fig. 4.1 for the quantum number v = 28, with
A and B being the classical turning points. In contrast, for v = 0 the
highest probability density is in the middle of the region.
The force constant k can be regarded as a measure for the strength of the
bond. Table 4.2 gives some typical values in the units of aJ Å−2 (= 102 N/m).
The values describe how k increases with the bond order. Molecules HCl,
19
Table 2.2: The force constants of some diatomic molecules.
Molecule k [aJ Å−2 ] Molecule k [aJ Å−2 ] Molecule k [aJ Å−2 ]
HCl
5.16
F2
4.45
CO
18.55
HF
9.64
O2
11.41
N2
22.41
Cl2
3.20
NO
15.48
HF, Cl2 and F2 have single bonds and relatively low values of k even though
k of HF is exceptionally high. The bond orders of O2 , NO, CO and N2 are
2, 2 21 , 3 and 3, respectively, and are reflected in the values of their force
constants. The force constant is affected by the delicate balance between
the attraction and repulsion forces in the molecule. These forces remain the
same in the isotopic substitution.
For vibrational levels, one often uses term values instead of energies. The
term values G(v) have the unit of wavenumber (cm−1 )
G(v) =
1
Ev
= ω(v + ),
hc
2
(2.9)
where ω is the wavenumber of vibration (often called improperly as vibrational frequency).
Exercise 4.1. Calculate the reduced masses of (a) 1 H81 Br and (b) 1 H127 I. The
wavenumbers of the vibrations of these molecules are (a) 2648.98 cm−1 and (b)
2308.09 cm−1 . Calculate the force constants of the bonds. Predict the vibrational
wavenumbers of the deuterium halides. m(81 Br)=80.9163 u, m(127 I)=126.9045 u,
m(1 H)=1.0078 u, m(2 H)=2.0141 u.
2.2
Anharmonicity
Figure 4.1 shows the potential energy, vibrational wavefunctions and energy levels of the harmonic oscillator. In reality, the vibrations of diatomic
molecules follow Hooke’s law, Eq. (4.1), relatively well only when the internuclear distance does not deviate largely from the equilibrium distance re ,
i.e. when x is small. We know that the molecule dissociates at large values
of r: two neutral atoms are formed and they do not affect each other any
20
Figure 2.2: The potential energy curve and energy levels of a diatomic
molecule when it behaves as an anharmonic oscillator. Dashed curves give
the same properties for a harmonic oscillator.
longer. Then the force constant is zero and r can be increased to infinity
without influencing the potential energy V . This is illustrated in Fig. 4.2.
The potential energy curve levels at a value V = De , where De is the dissociation energy as measured from the potential energy at the equilibrium
distance. Thus for r > re , the potential energy becomes lower than in the
case of the harmonic oscillator. At small values of r, the positive charges
of the nuclei cause a repulsion that opposes bringing the nuclei closer each
other and the potential energy curve is steeper than that of the harmonic
oscillator.
Anharmonicity changes the wavefunctions and term values. The term
values of the harmonic oscillator in Eq. (4.9) become a power series in (v +
1/2)
1
1
1
G(v) = ωe (v + ) − ωe xe (v + )2 + ωe ye (v + )3 + . . .
2
2
2
(2.10)
where ωe is the vibrational wavenumber that a classical oscillator would
have infinitely close to the equilibrium position. ωe xe , ωe ye . . . are anharmonicity constants. The terms ω, ωe xe , ωe ye . . . in the series (2.10) become
21
fast smaller. For example for HCl ωe =2990.946 cm−1 , ωe xe =52.8186 cm−1 ,
ωe ye =0.2244 cm−1 and ωe ze =-0.0122 cm−1 . The value of ωe xe is always positive, which makes the energy levels to approach each other when v increases.
These energy levels are compared with those of the harmonic oscillator in
Fig. 4.2. The levels of the anharmonic oscillator converge to the dissociation
limit De , above which they have a continuous distribution (continuum).
ωe can no longer be measured directly. The wavenumber differences
∆Gv+1/2 for vibrational transitions (v +1)−v are obtained from the equation
∆Gv+1/2 = G(v + 1) − G(v)
= ωe − ωe xe (2v + 2) + ωe ye (3v 2 + 6v +
13
)
4
+ ...
(2.11)
The wavenumbers of at least two transitions (e.g. G(1) − G(0) = ω0 and
G(2) − G(1) = ω1 ) are required to determine ωe and ωe xe .
For the dissociation energy De
De '
ωe2
,
4ωe xe
(2.12)
where the approximately sign results from the neglect of the anharmonicity
constants other than ωe xe .
Example 4.1 Calculate ωe , ωe xe and dissociation energy De for the electronic
ground state of the CO molecule from the following differences between the vibrational levels:
v 0 − v 00
1−0 2−1 3−2 4−3 5−4 6−5
G(v + 1) − G(v)[cm−1 ] 2143.1 2116.1 2088.9 2061.3 2033.5 2005.5
Solution. By neglecting ωe ye and higher terms in Eq. (2.11) we obtain
G(v + 1) − G(v) = ωe − 2ωe xe (v + 1).
We draw G(v + 1) − G(v) as a function of (v + 1), which produces a straight line
with a slope of −2ωe xe and a crossing point of ωe with the y-axis.
Fitting a straight line to the points with a computer gives
ωe = 2171.4 ± 0.4 cm−1
ωe xe = 13.8 ± 0.1 cm−1
The given uncertainties are standard deviations. The dissociation energy
De '
ωe2
' 85400 cm−1 ' 10.6 eV.
4ωe xe
22
Experimentally, the dissociation energy can only be measured with respect to the zero-point energy D0 . It is obvious from Fig. 4.2 that
D0 =
X
∆Gv+1/2 .
(2.13)
v
Experimental values for ∆Gv+1/2 with large quantum numbers of v cannot generally be determined with infrared and Raman spectroscopy, because
the intensities of the transitions with ∆v = ±2, ±3, . . . are weak and the
populations of highly excited vibrational states is low. Information about
higher vibrational levels can mostly be obtained from transitions between
electronic states.
The dissociation energy De is the same for the different isotopes of the
same molecule because the potential energy curve and, consequently, the
force constant do not depend on the neutron number. On the other hand,
the vibrational energy levels change, as ω depends on the mass as µ−1/2 (µ
is the reduced mass), resulting in the change of D0 in different isotopes.
Morse suggested in 1929 that
V (x) = De [1 − exp(−ax)]2
(2.14)
would be a useful potential energy function for an anharmonic oscillator. In
the Morse potential a and De are characteristic constants of the electronic
state. For this function, V (x) → De , when x → ∞, as it should. On the
other hand, when r → 0 (i.e. x → −re ), V (x) becomes large but not infinite.
This deficit in the Morse potential is not very serious, since the region where
r → 0 is not experimentally important. The vibrational term values obtained
using the Morse potential only include the terms (v + 1/2) and (v + 1/2)2 in
Eq. (4.10). Even though the quantitative use of the potential is limited, its
ease of use has made it popular compared to more accurate, but also more
complicated functions.
2.3
The potential energy curves of excited
states
Each excited electronic state has its own potential energy curve, which in
most cases looks similar to the potential energy curve of the ground state.
23
Figure 2.3 shows the potential energy curves for the ground state and excited electronic states of the short-lived molecule C2 . The ground electron
configuration of C2 is
(σg 1s)2 (σu∗ 1s)2 (σg 2s)2 (σu∗ 2s)2 (πu 2p)4 (σg 2p)0 ,
(2.15)
which gives the ground state X 1 Σ+
g . The lowest electronic states are formed
from the electron configurations when an electron from the πu 2p- or σu∗ 2sorbital has been promoted to the σg 2p-orbital. The information in Fig. 2.3
has been obtained by observing absorption and emission spectra using different techniques.
When C2 dissociates the two carbon atoms released can be either in the
ground state or in excited states. The ground electron configuration of the C
atom, 1s2 2s2 2p2 , gives three terms 3 P , 1 D and 1 S in the order of increasing
energy. Figure 2.3 shows that six of the states of C2 dissociate producing
both C atoms with term 3 P . Other states give dissociation products where
one or both of the carbon atoms have the term symbols 1 D or 1 S.
Like in the ground state, a molecule can vibrate and rotate in the electronically excited states. The total term value (or total energy)
S = T + G(v) + F (J),
(2.16)
is the sum of the electronic term value T , vibrational term value G(v) and
rotational term value F (J). The vibrational term value can be obtained
from Eq. (4.10), but the wavenumber ωe and the anharmonicity constants
ωe xe , ωe ye , . . . are different for different excited states. Figure 2.3 also shows
that the equilibrium distances re are different.
24
Figure 2.3: The potential energy curves of the C2 molecule for the ground
state and several excited states.
25
Chapter 3
Electronic transitions in
diatomic molecules
3.1
On the coupling of angular momenta
The orbital motion and spin of each electron induce magnetic momenta that
behave like small bar magnets. The way in which magnets interact with
each other corresponds to coupling of angular momenta. For all diatomic
molecules, the coupling mechanism that describes best the electronic states
is similar to the LS coupling in atoms. We have already already talked about
this in Chapter 2. Figure 5.1(a) shows how the orbital angular momenta of
each electrons are coupled together to form the resultant L whose component
along the internuclear axis is Λh̄. Similarly, the spins of individual electrons
couple to give S to give the component Σh̄ along the axis. The quantum
number Σ can have values
Σ = S, S − 1, . . . − S.
(3.1)
S remains a good quantum number.
We can couple Λh̄ and Σh̄ together to get the component of the total
angular momentum along the axis, Ωh̄. This way of coupling is known as
Hund’s case (a). The quantum number Ω can be obtained from the equation
Ω = Λ + Σ.
(3.2)
For the 2 Π molecule NO, for instance, for which Λ = ±1 and Σ = ± 12 , Ω can
take the values ± 12 , ± 32 . Term symbols are written in this case as 2 Π 1 and
2
2
Π3 .
2
26
Figure 3.1: (a) Hund’s case (a) and (b) Hund’s case (c) to couple the total
angular momentum and total spin of a diatomic molecule.
Hund’s case (a) is the most common, but it is still an approximation,
as all couplings of angular momenta. If a molecule has at least one heavy
nucleus, the spin-orbit interaction is so strong that the electron spin and
angular momenta couple to give the resultant J. This angular momentum has
a component Ωh̄ on the internuclear axis, so Ω is a good quantum number,
but Λ and Σ are not. This coupling approximation is known as Hund’s case
(c) and it is presented in Fig. 3.1(b).
3.2
Selection rules in general
The selection rules for the orbital parts of the wavefunctions of two electronic states depend totally on symmetry properties. Electronic transitions
are mainly caused by the interaction of the electronic component of electromagnetic radiation with a molecule. The selection rules are therefore for the
electric dipole transitions.
The intensity of an electronic transition is proportional to the square of
the transition dipole moment Re , where
Re =
Z
ψe0∗ µ̂ψe00 dτe .
(3.3)
For an allowed transition |Re | =
6 0. The symmetry requirement is
Γ(ψe0 ) × Γ(µ) × Γ(ψe00 ) = A
27
(3.4)
for a transition between non-degenerate states and
Γ(ψe0 ) × Γ(µ) × Γ(ψe00 ) ⊃ A
(3.5)
for a transition between states, from which at least one is degenerate. The
symbol ⊃ means ’is included’. A is the totally symmetric symmetry species
of the point group in question.
The components of the transition dipole moment Re along the Cartesian
axes are
R
Re,x = R ψe0∗ µx ψe00 dτe
Re,y = R ψe0∗ µy ψe00 dτe
(3.6)
0∗
00
Re,z =
ψe µx ψe dτe .
Since
|Re |2 = (Re,x )2 + (Re,y )2 + (Re,z )2 ,
(3.7)
an electronic transition is allowed, if any of the terms Re,x , Re,y or Re,z is
different from zero. Thus, we must have for a transition to be allowed
Γ(ψe0 ) × Γ(Tx ) × Γ(ψe00 ) = A
and/or Γ(ψe0 ) × Γ(Ty ) × Γ(ψe00 ) = A
and/or Γ(ψe0 ) × Γ(Tz ) × Γ(ψe00 ) = A
(3.8)
when a transition is between non-degenerate states. Tx , Ty , and Tz are the
translations along the respective axes. In case of a degenerate state, ’=’ is
replaced by ’⊃’ in the above equation.
If the product of two symmetry species is totally symmetric, the symmetry species must be the same. Thus Eq. (3.8) can be written
Γ(ψe0 ) × Γ(ψe00 ) = Γ(Tx ) and/or Γ(Ty ) and/or Γ(Tz ).
(3.9)
If a degenerate state is involved, ’=’ is replaced by ’⊃’ in the above equation. This is a general selection rule for an electronic transition between two
electronic states.
3.2.1
Selection rules for diatomic molecules
The dipole selection rules for diatomic molecules can be summarized (apart
from the spin selection rule, they can be obtained from the above treatment):
1. ∆Λ = 0, ±1
(5.10)
For example, Σ − Σ, Π − Σ and ∆ − Π transitions are allowed but ∆ − Σ
or Φ − Π transitions are not allowed.
28
2. ∆S = 0
(5.11)
This selection rule breaks down when the nuclear charge becomes large.
For example, triplet-singlet transitions are absolutely forbidden in H2 ,
but in CO the a3 Π − X 1 Σ+ transition is observed but weak.
3. ∆Σ = 0;
∆Ω = 0, ±1
between the components of the same multiplet.
(5.12)
4. + ←→ −;
+ ←→ +;
− ←→ −
(5.13)
This is relevant only for Σ−Σ transitions so that Σ+ −Σ+ and Σ− −Σ−
transitions are allowed.
5. g ←→ u;
g ←→ g;
u ←→ u
(5.14)
+
+
+
+
For example, Σg − Σg transitions are forbidden, but Σu − Σg and
Πu − Σ+
g are allowed.
In Hund’s case (c) (Fig. 3.1b) the selection rules are slightly different.
The rules (5.11) and (5.14) still valid, but since Λ and Σ are no longer good
quantum numbers, the rules (5.10) and (5.12) do not work. The applicability
of the rule (5.13) becomes more limited.
+
Exercise 5.1. Using Eq. (3.8) or Eq. (3.9) show that a Σ+
g → Σu is allowed in
a diatomic homonuclear molecule (like O2 ). The relevant character table is given
on page 25. Note that the translations are marked as x, y, and z in that table.
3.3
Vibronic transitions
Figure 3.2 displays the vibrational energy levels related to two electronic
states. We assume that the electronic transition between the states is allowed.
The vibrational levels of the upper (lower) states are denoted with quantum
numbers v 0 (v 00 ). In the electronic spectrum, there are no selection rules that
would limit the value of ∆v, but the Franck-Condon principle set the limits
for the intensities of the transitions.
Vibrational transitions that occur during electronic transitions are called
vibronic transitions. These vibronic transitions (with related rotational transitions) give rise to bands in the spectrum. A set of bands belonging to one
electronic transitions is called an electronic band system. Vibronic transitions
can be divided into progressions and sequences that have been illustrated in
29
Figure 3.2: Progressions and sequences in the electron spectrum of a diatomic
molecule.
Fig. 3.2. A progression includes a series of vibronic transitions that have a
common upper or lower vibrational level. A group of vibrations for which
∆v is constant forms a sequence.
A symbol to denote a vibronic transition is v 0 − v 00 where v 0 and v 00 are
the vibrational quantum numbers of the upper and lower states, respectively.
This follows the convention in spectroscopy. Thus a purely electronic transition is written 0 − 0.
3.4
The Franck-Condon principle
In 1925, before the presentation of the Schrödinger equation, Franck studied
different intensity distributions of vibronic transitions. His conclusions were
based on the fact that the electronic transition takes place much faster than
the vibration of the molecule. Therefore in a vibronic transition the nuclei
have very accurately the same locations and velocities before and after the
transition. The possible consequences are illustrated in Fig. 3.3 that shows
the potential energy curves of two electronic states. The curves are plotted
so that re0 > re00 .
30
Figure 3.3: The Franck principle when (a) re0 > re00 and (b) re0 ' re00 . The
vibronic transition B–A is the most probable in each case.
In an absorption process of Fig. 3.3(a) the transition goes from the point
A in the lower state to the point B in the upper state. (Zero-point energy
can be neglected when considering Franck’s semiclassical arguments.) The
requirement on the same location before and after the transition means that
the transition occurs between the points that are on the same vertical line.
Then r remains constant, and we speak of a vertical transition. The requirement on the same velocity means that the transition from point A, where
the nuclei do not move, must go to point B, which is a classical turning point
and where the nuclei also are motionless. The transition from A to C is very
improbable because the change in r is very large. The transition from A to
D is also improbable, even though r is the same the nuclei are moving in
point D.
In Fig. 3.3(b) re0 ' re00 . Now the most probable transition is from point A
to B without any vibrational energy in the upper state. A transition from A
to C keeps the same r, but the velocities of the nuclei have increased, because
they have kinetic energy corresponding to the distance BC.
Condon treated the intensities of vibronic transitions quantum mechan-
31
ically in 1928. The intensity is proportional to the square of the transition
dipole moment Rev (see Eq. (3.13))
Rev =
Z
0∗
00
ψev
µ̂ψev
dτev ,
(3.15)
0
00
where µ̂ is the electric dipole moment operator, and ψev
and ψev
are the vibronic wavefunctions of the upper and lower states, respectively. Integration
is over the electronic and vibrational coordinates. Assuming that the BornOppenheimer approximation is valid, ψev can be represented as a product
ψe ψv . Then it follows from Eq. (3.15) that
Rev =
Z Z
ψe0∗ ψv0 µ̂ψe00 ψv00 dτe dr,
(3.16)
where r is the internuclear distance. We integrate first over the electronic
coordinates τe
Z
Rev = ψv0 Re ψv00 dr,
(3.17)
where Re is the electric transition dipole moment:
Re =
Z
ψe0∗ µ̂ψe00 dτe .
(3.18)
The possibility to carry out the integration to give Eq. (3.17) results from the
Born-Oppenheimer approximation which assumes that nuclei can be treated
as stationary with respect to much faster electrons. This approximation also
allows us to take out Re from the integral (3.17) and treat it as a constant
that does not depend on r. We obtain then
Rev = Re
Z
ψv0 ψv00 dr.
(3.19)
The integral ψv0 ψv00 dr is a measure for the overlap of the two vibrational
wavefunctions. Its square is known as the Franck-Condon factor.
In quantum mechanics, the classical turning point of a vibration is replaced by the maximum or minimum of the wavefunction ψv close to this
turning point. Figure 3.4 presents a case where the the vibrational wavefunction of the upper state v 0 = 4 has a maximum close to the turning point
and is directly above the maximum of the wavefunction v 00 = 0. The largest
contribution to the overlap integral of the vibrational wavefunctions is indicated by a solid line, but considerable overlap occurs when r is between
R
32
Figure 3.4: The Franck-Condon principle applied to the case re0 > re00 when
the 4 − 0 transition is the most probable.
33
Figure 3.5: Typical intensity distributions for vibronic transitions.
the dashed lines. Clearly, the overlap is considerable also for wavefunctions
whose v 0 is close to four. We get an intensity distribution shown in Fig.
3.5(b).
If re0 re00 , a large fraction of the intensity may go the vibrational states in
the continuum above the the dissociation limit. A progression (from the lower
state v 00 = 0) shown in Fig. 3.5(c) then follows, with an intensity maximum
at high values of v 0 or in the continuum. Figure 3.5(a) shows the intensity
maximum to the vibrational state v 0 = 0, when re0 ' re00 . The intensity falls
usually down rapidly in such a case.
The case with re0 < re00 can happen if an electron makes a transition from
an antibonding or non-bonding orbital to a bonding orbital. It is most likely
between two excited electronic state. The situation is similar to the one in
Fig. 3.4, but the upper potential energy curve is shifted to a smaller value of r,
for example, in such a way that the right maximum of the wavefunction v 0 = 4
is above the maximum of v 00 = 0. A result is the intensity distribution in Fig.
3.5(b). Thus the observation of the intensity maximum at the vibrational
quantum number v 0 > 0 indicates a substantial change in the equilibrium
distance re between the upper and lower states, but it does not tell the sign
of the change. This is quantitatively quite not true because the progressions
are slightly different for the cases re0 > re00 and re0 < re00 . The analysis of the
intensities of the vibronic transitions yields a lot of information about the
shapes of the potential energy curves of the electronic states.
34
Figure 3.6: The repulsive ground state and the bound excited state of the
He2 molecule.
Repulsive states and continuous spectra
The ground electron configuration (1σg 1s)2 (1σu∗ 1s)2 of the He2 molecule is
expected to be unstable, because the bonding character of the σg 1s orbital
is cancelled by the antibonding character of the σu∗ 1s orbital. The potential
energy curve of the X 1 Σ+
g state has no minimum but it decreases gradually
as a function of r. This is shown in Fig. 3.6. Such a state is called repulsive,
because the atoms repel each other. The state has no discrete vibrational
energy levels but the levels form a continuum.
By promoting an electron from the σu∗ orbital to an binding orbital can
give bound states of the He2 molecule. Several of them have been observed in
emission spectroscopy. For example, the configuration (σg 1s)2 (σu∗ 1s)1 (σg 2s)1
3 +
leads to the bound states A1 Σ+
u and a Σu . Figure 3.6 shows the shape of the
potential energy curve of the A1 Σ+
u state. The transition A − X is allowed
and produces a strong continuous intensity in the wavelength region 60–100
nm. This can be used as a source of far ultraviolet radiation, like other
diatomic noble-gas molecules.
35