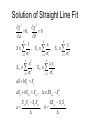Download week 11 - NUS Physics

Chapter 15
Modeling of Data
Statistics of Data
1 N
• Mean (or average): x   x j
N j 1
• Variance:   Var( x1 ,
2
2
1 N
, xN ) 
xj  x 


N  1 j 1
• Median: a value xj such that half of the
data are bigger than it, and half of data
smaller than it.
σ is called standard deviation.
Higher Moments
Skew( x1 ,
1
, xN ) 
N
 xj  x 



 
j 1 
Kurt( x1 ,
 1
, xN )  
 N
 xj  x 




j 1 

N
N
3
4

3

Gaussian Distribution

1
N ( x; a,  ) 
e
 2
x a
Var( x)   2
Skew( x)  0
Kurt( x)  0
( x  a )2
2 2
Least Squares
• Given N data points (xi,yi), i = 1, …, N, find
the fitting parameters aj, j = 1, 2, …, M of
the function
f(x) = y(x; a1,a2,…,aM)
such that
N
  y  y( x ; a ,
i 1
i
i
1
, aM ) 
2
is minimized over the parameters aj.
Why Least Squares
• Given the parameters, what is the
probability that the observed data
occurred?
• Assuming independent, Gaussian
distribution, that is:


 1  y  y ( x ) 2 
i
P   exp    i
  yi 
2
i

i 1 
 



N
Chi-Square Fitting
• Minimize the quantity:
 yi  y ( xi ; a1 ,
  
i
i 1 
N
2
, aM ) 


2
• If each term is an independent Gaussian, 2
follows so-called 2 distribution. Given the
value 2 above, we can compute Q =
Prob(random variable chi2 > 2)
• If Q < 0.001 or Q > .999, the model may be
rejected.
Meaning of Goodness-of-Fit Q
P(  )  
2
 2

exp   / 2
2
Observed
value of 2

If the statistic 2 indeed
follows this distribution,
the probability that chisquare value is the
currently computed value
2, or greater, equals the
hashed area Q.
It is quite unlikely if Q is
very small or very close to
1. If so, we reject the
model.
Area = Q
0
2
Number of degrees of
freedom  = N – M.
Fitting to Straight Line
(with known error bars)
y
Given (xi, yi±σi)
Find interception a and slope
b such that
 yi  a  bxi 
2
 ( a, b)   

i
i 1 

N
2
the chi-square merit function
is minimized.
Goodness-of-fit is
Q=gammq((N-2)/2, 2/2). If
Q > 0.1, the fitting is good, if
Q ≈ 0.001, may be OK, but if
Q < 0.001, fitting is
questionable.
fitting to y=a+bx
x
If Q > 0.999, fitting is too
good to be true.
Linear Regression Model
Error in y, but no
error in x.
y
ε
fitting to y=a+bx
x
Data do not
follow exactly
the straight line.
The basic
assumption in
linear
regression
(least squares
fit) is that the
deviations ε are
independent
gaussian
random noise.
Solution of Straight Line Fit
 2
 2
 0,
0
a
b
N
N
N
xi
yi
1
S   2 , Sx   2 , S y   2
i 1
i
N
S xx  
i 1
xi2
i 1 
2
i
i
N
, S xy  
i 1
i 1
xi yi
 i2
aS  bS x  S y
aS x  bS xx  S xy ,   SS xx  S x2
a
S xx S y  S x S xy

, b
SS xy  S x S y

i
Error Propagation
• Let z = f(y1,y2,…,yN) be a function of
independent random variables yi.
Assuming the variances are small, we
have N
f
zz 
( yi  yi )
i 1 yi y
i
• Variance of z is related to variances of yi
by 2 N 2  f 2
 f   i 
i 1

 yi 
Error Estimates on a and b
• Using error propagation formula, viewing a
as a function of yi, we have
a S xx  S x xi

2
yi
i 
• Thus
2
 S xx  S x xi 
S xx
   
 
2

i 1
 i  
N
2
a
• Similarly
2
i
S
 

2
b
What if error in yi is unknown?
• The goodness-of-fit Q can no longer be
computed
• Assuming all data have same σ:
N
    yi  y ( xi )  /( N  M )
2
i 1
2
M is number of basis functions,
M=2 for straight line fit.
• Error in a and b can still be estimated,
using σi=σ (but less reliably)
General Linear Least-Squares
• Fit to a linear combination of arbitrary
functions:
M
y ( x)   ak X k ( x)
k 1
• E.g., polynomial fit Xk(x)=xk-1, or harmonic
series Xk(x)=sin(kx), etc
• The basis functions Xk(x) can be nonlinear
Merit Function & Design Matrix
• Find ak that minimize
 yi   ak X k ( xi ) 
k 1

2  
i

i 1 

M
N
• Define
Aij 
X j ( xi )
i
, bi 
yi
i
2
 a1

Let a be a
a2

column vector: a 


 aM
• The problem can be stated as
Min || b  Aa ||2






Normal Equation & Covariance
• The solution to min ||b-Aa|| is ATAa=ATb
• Let C = (ATA)-1, then a = CATb
• We can view data yi as a random variable
due to random error, yi=y(x)+εi. <εi>=0,
<εiεj>=σi2 ij. Thus a is also a random
variable. Covariance of a is precisely C
• <aaT>-<a><aT> = C
• Estimate of the fitting coefficient is
a j  CAT b   C jj
j
Singular Value Decomposition
• We can factor arbitrary complex matrix as
A = UΣV†
 a11
a
 21


 aN 1
NM
a1M  U11
 U
   21
 
 
aNM  
NN
U1N   w1
 0



U NN   0
U and V are unitary, i.e., UU†=1, VV†=1
Σ is diagonal (but need not square), real and
positive, wj ≥ 0.
NM
0
0
0 
V11

0 
V12

wM 
 
0 
MM
VM 1 


VMM 
Solve Least-Squares by SVD
• From normal equation, we have
a  ( AT A) 1 AT b
( AB)T  BT AT
but A  U V
( AB)1  B 1 A1
T


 V  U U V  V  U
so a  (U V ) U V
T T
T
T
T
T
1
1
(U V T )T b
T
T

b  V  V
T
T

1
V TU T b
 V (T ) 1V TV TU T b  V (T ) 1 TU T b
Or
a


w j  , j 1,
 UT( j )  b 

 V( j )
wj 
,M 
Omitting terms with very
small w gives robust method.
Nonlinear Models y=y(x; a)
• 2 is a nonlinear function of a. Close to
minimum, we have (Taylor expansion)
 2 (a)   (a min )  (a  a min )T  D  (a  a min )  O  (a  a min )3 
1
2
1 T
T
   d a  a  Da
2
where
d +D  a = 2 (a),
 2  2 (a)
Dij 
ai a j
Solution Methods
• Know gradient only, Steepest descent:
a next  acur  constant  (acur )
2
• Know both gradient and Hessian matrix:
a min  acur  D1  2 (acur )
• Define
N
1
1  y( xi ; a) y( xi ; a) 
2
β    ,  kl   2 

2


a

a
i 1
i 
k
l

Levenberg-Marquardt Method
• Smoothly interpolate between the two
methods by a control parameter . =0,
use more precise Hessian;  very large,
use steepest descent.
• Define new matrix A’ with elements:
 ii (1   ), if i  j
ij  
if i  j
ij ,
Levenberg-Marquardt Algorithm
•
•
•
•
•
Start with an initial guess of a
Compute 2(a)
Pick a modest value for , say =0.001
(†) Solve A’a=β, evaluate 2(a+a)
If 2 increase, increase  by a factor of 10
and go back to (†)
• If 2 decrease, decrease  by a factor of
10, update a  a+ a, and go back to (†)
Problem Set 9
1. If we use the basis
{1, x, x + 2}
for a linear least-squares fit using normal
equation method, do we encounter
problem? Why? How about SVD?
2. What happen if we apply the LevenbergMarquardt method for a linear leastsquare problem?