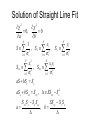* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download week 11 - NUS Physics
Survey
Document related concepts
Transcript
Chapter 15
Modeling of Data
Statistics of Data
1 N
• Mean (or average): x x j
N j 1
• Variance: Var( x1 ,
2
2
1 N
, xN )
xj x
N 1 j 1
• Median: a value xj such that half of the
data are bigger than it, and half of data
smaller than it.
σ is called standard deviation.
Higher Moments
Skew( x1 ,
1
, xN )
N
xj x
j 1
Kurt( x1 ,
1
, xN )
N
xj x
j 1
N
N
3
4
3
Gaussian Distribution
1
N ( x; a, )
e
2
x a
Var( x) 2
Skew( x) 0
Kurt( x) 0
( x a )2
2 2
Least Squares
• Given N data points (xi,yi), i = 1, …, N, find
the fitting parameters aj, j = 1, 2, …, M of
the function
f(x) = y(x; a1,a2,…,aM)
such that
N
y y( x ; a ,
i 1
i
i
1
, aM )
2
is minimized over the parameters aj.
Why Least Squares
• Given the parameters, what is the
probability that the observed data
occurred?
• Assuming independent, Gaussian
distribution, that is:
1 y y ( x ) 2
i
P exp i
yi
2
i
i 1
N
Chi-Square Fitting
• Minimize the quantity:
yi y ( xi ; a1 ,
i
i 1
N
2
, aM )
2
• If each term is an independent Gaussian, 2
follows so-called 2 distribution. Given the
value 2 above, we can compute Q =
Prob(random variable chi2 > 2)
• If Q < 0.001 or Q > .999, the model may be
rejected.
Meaning of Goodness-of-Fit Q
P( )
2
2
exp / 2
2
Observed
value of 2
If the statistic 2 indeed
follows this distribution,
the probability that chisquare value is the
currently computed value
2, or greater, equals the
hashed area Q.
It is quite unlikely if Q is
very small or very close to
1. If so, we reject the
model.
Area = Q
0
2
Number of degrees of
freedom = N – M.
Fitting to Straight Line
(with known error bars)
y
Given (xi, yi±σi)
Find interception a and slope
b such that
yi a bxi
2
( a, b)
i
i 1
N
2
the chi-square merit function
is minimized.
Goodness-of-fit is
Q=gammq((N-2)/2, 2/2). If
Q > 0.1, the fitting is good, if
Q ≈ 0.001, may be OK, but if
Q < 0.001, fitting is
questionable.
fitting to y=a+bx
x
If Q > 0.999, fitting is too
good to be true.
Linear Regression Model
Error in y, but no
error in x.
y
ε
fitting to y=a+bx
x
Data do not
follow exactly
the straight line.
The basic
assumption in
linear
regression
(least squares
fit) is that the
deviations ε are
independent
gaussian
random noise.
Solution of Straight Line Fit
2
2
0,
0
a
b
N
N
N
xi
yi
1
S 2 , Sx 2 , S y 2
i 1
i
N
S xx
i 1
xi2
i 1
2
i
i
N
, S xy
i 1
i 1
xi yi
i2
aS bS x S y
aS x bS xx S xy , SS xx S x2
a
S xx S y S x S xy
, b
SS xy S x S y
i
Error Propagation
• Let z = f(y1,y2,…,yN) be a function of
independent random variables yi.
Assuming the variances are small, we
have N
f
zz
( yi yi )
i 1 yi y
i
• Variance of z is related to variances of yi
by 2 N 2 f 2
f i
i 1
yi
Error Estimates on a and b
• Using error propagation formula, viewing a
as a function of yi, we have
a S xx S x xi
2
yi
i
• Thus
2
S xx S x xi
S xx
2
i 1
i
N
2
a
• Similarly
2
i
S
2
b
What if error in yi is unknown?
• The goodness-of-fit Q can no longer be
computed
• Assuming all data have same σ:
N
yi y ( xi ) /( N M )
2
i 1
2
M is number of basis functions,
M=2 for straight line fit.
• Error in a and b can still be estimated,
using σi=σ (but less reliably)
General Linear Least-Squares
• Fit to a linear combination of arbitrary
functions:
M
y ( x) ak X k ( x)
k 1
• E.g., polynomial fit Xk(x)=xk-1, or harmonic
series Xk(x)=sin(kx), etc
• The basis functions Xk(x) can be nonlinear
Merit Function & Design Matrix
• Find ak that minimize
yi ak X k ( xi )
k 1
2
i
i 1
M
N
• Define
Aij
X j ( xi )
i
, bi
yi
i
2
a1
Let a be a
a2
column vector: a
aM
• The problem can be stated as
Min || b Aa ||2
Normal Equation & Covariance
• The solution to min ||b-Aa|| is ATAa=ATb
• Let C = (ATA)-1, then a = CATb
• We can view data yi as a random variable
due to random error, yi=y(x)+εi. <εi>=0,
<εiεj>=σi2 ij. Thus a is also a random
variable. Covariance of a is precisely C
• <aaT>-<a><aT> = C
• Estimate of the fitting coefficient is
a j CAT b C jj
j
Singular Value Decomposition
• We can factor arbitrary complex matrix as
A = UΣV†
a11
a
21
aN 1
NM
a1M U11
U
21
aNM
NN
U1N w1
0
U NN 0
U and V are unitary, i.e., UU†=1, VV†=1
Σ is diagonal (but need not square), real and
positive, wj ≥ 0.
NM
0
0
0
V11
0
V12
wM
0
MM
VM 1
VMM
Solve Least-Squares by SVD
• From normal equation, we have
a ( AT A) 1 AT b
( AB)T BT AT
but A U V
( AB)1 B 1 A1
T
V U U V V U
so a (U V ) U V
T T
T
T
T
T
1
1
(U V T )T b
T
T
b V V
T
T
1
V TU T b
V (T ) 1V TV TU T b V (T ) 1 TU T b
Or
a
w j , j 1,
UT( j ) b
V( j )
wj
,M
Omitting terms with very
small w gives robust method.
Nonlinear Models y=y(x; a)
• 2 is a nonlinear function of a. Close to
minimum, we have (Taylor expansion)
2 (a) (a min ) (a a min )T D (a a min ) O (a a min )3
1
2
1 T
T
d a a Da
2
where
d +D a = 2 (a),
2 2 (a)
Dij
ai a j
Solution Methods
• Know gradient only, Steepest descent:
a next acur constant (acur )
2
• Know both gradient and Hessian matrix:
a min acur D1 2 (acur )
• Define
N
1
1 y( xi ; a) y( xi ; a)
2
β , kl 2
2
a
a
i 1
i
k
l
Levenberg-Marquardt Method
• Smoothly interpolate between the two
methods by a control parameter . =0,
use more precise Hessian; very large,
use steepest descent.
• Define new matrix A’ with elements:
ii (1 ), if i j
ij
if i j
ij ,
Levenberg-Marquardt Algorithm
•
•
•
•
•
Start with an initial guess of a
Compute 2(a)
Pick a modest value for , say =0.001
(†) Solve A’a=β, evaluate 2(a+a)
If 2 increase, increase by a factor of 10
and go back to (†)
• If 2 decrease, decrease by a factor of
10, update a a+ a, and go back to (†)
Problem Set 9
1. If we use the basis
{1, x, x + 2}
for a linear least-squares fit using normal
equation method, do we encounter
problem? Why? How about SVD?
2. What happen if we apply the LevenbergMarquardt method for a linear leastsquare problem?