* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Quantum non-‐equilbrium dynamics in closed systems. - Indico
Hydrogen atom wikipedia , lookup
Renormalization group wikipedia , lookup
Quantum key distribution wikipedia , lookup
Particle in a box wikipedia , lookup
Renormalization wikipedia , lookup
Dirac bracket wikipedia , lookup
Quantum state wikipedia , lookup
Ising model wikipedia , lookup
Density matrix wikipedia , lookup
Perturbation theory (quantum mechanics) wikipedia , lookup
Relativistic quantum mechanics wikipedia , lookup
Scalar field theory wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Symmetry in quantum mechanics wikipedia , lookup
Canonical quantization wikipedia , lookup
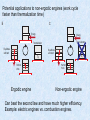
Quantum non-‐equilbrium dynamics in closed systems. Anatoli Polkovnikov, BU Par>al list of recent collaborators L. D’Alessio Y. Kafri A. Katz M. Kolodrubetz P. Mehta M. Rigol L. Santos BU, PennState Technion BU BU BU PennState Yeshiva Non-‐equilibrium phenomena in CM and ST, ICTP, Trieste, 07/03/2014 Brief Outline • ETH and thermodynamics • Relaxa>on in integrable and weakly non-‐integrable systems • Emergence of macroscopic Hamiltonian dynamics from non-‐adiaba>c response • Extension of Kibble-‐Zurek mechanism to dynamical fields. Dynamical localiza>on transi>on near quantum cri>cal points. • Floquet systems Non-‐equilibrium quantum systems J. Von Neumann: Non-‐equilibrium theory is a “theory of non-‐elephants”. • Chaos and thermaliza>on in classical and quantum isolated systems, mostly aQer sudden quenches • Relaxa>on in weakly interac>ng systems. Prethermaliza>on and the generalized Gibbs ensemble. • Steady states: phases and phase transi>ons in driven systems (isolated or dissipa>ve) • Many-‐body localiza>on: interplay of disorder and ergodicity • Universal non-‐equilibrium dynamics. • Dynamical phase transi>ons (in >me). • Many more: non-‐equilibrium Stat. Mech., biological systems, ac>ve maWer, … Classical chao>c systems 3 chaos implies strong usually exponential sensitivity of the trajectories to small perturbations. In Regular vs. chao>c mo>on: like beauty. When we see it we recognize it. 3 chaos implies strong usually exponential sensitivity of the trajectories to small perturbations. In No mathema>cally rigorous defini>on of chaos. Standard prac>cal defini>on: Divergent trajectories. FIG. 1 Examples of trajectories of a particle bouncing in a cavity (i) non-chaotic circular (top left image) The analysis of with φ = π is even simpler Kthe other attractor K2 ! λ1,2 = 1 + ± K+ . (I.15) 2 4 K K2 λ1,2 = 1 + ± K+ . 2 4 early for any positive K there are two real solutions with one larger than one. So this point is Clearly for any positive K there are two real solutions with one larger than one. So this p No chaos in one-‐dimension. ways unstable. This is not very surprising since this attractor corresponds to the situation, where always unstable. This is not very surprising since this to the situation, unique rela>on aattractor nd xfast . corresponds mass sits on top of the potential. It isEnsures interesting that if instead of bδetween kicks onepapplies periodic a mass sits on top of the potential. It is interesting that if instead of δ kicks one applies fast p otion of the pendulum: K = K0 + a sin(νt) then one can stabilize the top equilibrium φ = π. motion of the pendulum: K = K0 + a sin(νt) then one can stabilize the top equilibrium his is known as the Kapitza effect (or Kapitza pendulum) and there are many demonstrations This is known as the Kapitza effect (or Kapitza pendulum) and there are many demonst w it works. In Fig. 2 we show the phase space portrait of the kicked rotor at different values of how it works. In Fig. 2 we show the phase space portrait of the kicked rotor at different va . It is clear that as K increases the system becomes more and more chaotic. At K = Kc ≈ 1.2 K. It is clear that as K increases the system becomes more and more chaotic. At K = Kc ere is a delocalization transition, where the chaotic region becomes delocalized and the system there is a delocalization transition, where the chaotic region becomes delocalized and the creases its energy without bound. increases its energy without bound. Simplest chao>c system – kicked rotor (kicked Josephson junc>on). Break energy conserva>on by kicks. Equa>ons of mo>on: Chirikov standard map Transition from regular (localized) to chaotic Transition from regular (localized) to chaotic (delocalized) motion as K increases. Chirikov, (delocalized) motion as K increases. Chirikov, 1971 1971 K=0.5 K=0.5 K=K g=0.971635 K=Kg=0.971635 K=5 (images taken from scholarpedia.org) K=5 (images taken from scholarpedia.org) Quantum systems. Linear equa>ons of mo>on no chaos? Linear equa>ons of mo>on like harmonic chains are non-‐chao>c. Any solu>on is a superposi>on of normal modes (eigenstates). von Neumann (1929): chaos (and ergodicity) are encoded in observables. 13 Wigner (1955), thinking about spectrum of complex nuclei: Hamiltonians of the nuclei are essen>ally like random matrices. ese levels in thisis interval (e.g. over it. many nearby Any ini>al structure rapidly lost o nce we averaged start diagonalizing predic>on: level repulsion. Wigner-‐Dyson sta>s>cs (Wigner SIn urmize) ryFamous different from the Wigner - Dyson statistics. particular, miltonian is completely diagonal in the single-particle basis. interval δE = ω there are no levels is simply expressed by Non-‐chao>c “generic systems”. Expect Poisson sta>s>cs (Berry-‐Tabor conjecture, 1977) P0 (ω) = exp[−ω], (II.10) Surmize (II.7).some This statement in fact known in literature gure gives idea ofis how behave like a sequence of independent random variables (i.e. have Poisson statistics) hat the underlying classical dynamics is completely integrable. In Fig. 5 we show level Examples of level sta>s>cs 15 y = e−s FIG. 7 Sinai billiard, which is a classical chaotic systems, similar to the Bunimovich stadium considered arlier. Left panel illustrates the Billiard and the classical trajectory (image source Wikipedia). Right anel shows level spacing statistics for the same billiard together with the Poisson and the Wigner-Dyson istributions (image source O. Bohigas, M.J. Giannoni, C.7Schmit Phys. which Rev. Lett. 52, 1 chaotic (1984)).systems, similar to the Bunimovich stadium considered FIG. Sinai billiard, is a classical s=0 1 2 3 4 earlier. Left panel illustrates the Billiard and the classical trajectory (image source Wikipedia). Righ the Wigner-Dyson statistics. Incommensurate 2D box. Sinai Billiard. O. for Bohigas et. atogether l. 1984 statistics the same billiard with the Poisson and the Wigner-Dyson of eigenvalues π (m /a + n /b ) of a Notices the AMS 55, 32 (2008)). The levels are given by a simple formula: E (image = distributions sourcechaotic O. Bohigas, M.J. also Giannoni, C. Schmit Phys. Rev. Lett. 52, 1 (1984)). Z. R 2another 008 nhaos?, Fig. 8udnik, weof show example of the level statistics for a classical system analyzed rectangle with sufficiently incommensurable √ nergy levels in classical chaotic ratio systems are typically well described by Figure It is conjectured the distribution panel shows level el statistics in 3. a rectangular cavity with thethat of sides a/b = 4 5 (Z. Rudnick, What Is spacing 2 2 2 2 2 n,m n2 /b2 ). sides a, b is that of a Poisson process. The mean is 4π /ab by simple geometric reasoning, energy levels√in classical chaotic systems are typically well described by the Wigner-Dyson statistics or a in rectangular cavity with a and asymptotic b, which have the following ratio: a/b = 4 5. ties in the spectrum, P (s) collapses to a point conformity withsides Weyl’s formula. massfor at the origin. Deviations are also seen in the In Fig. 8 we show another example of the level statistics a classical chaotic system also analyzed Here are plotted the statistics ofYet the y agree perfectly well with the Poisson statistics. thegaps Berry-Tabor conjecture is not chaotic case in arithmetic examples. Nonetheless, (1, 1) empirical studies offer tantalizing evidence for λi+1 − λi found for rthe first 250,000 the “generic” truth of the conjectures, as Figures 0.4 3 and 4 show. eigenvalues of a rectangle with side/bottom ties √ GOE distribution Some progress on the Berry-Tabor conjecture in 4 ma ratio 5 and area 4π , binned into intervals of the case of the rectangle billiard has been achieved r cha 0.7 (1, 1) by Sarnak, by Eskin, Margulis, and Mozes, and by emp 0.1, compared to the expected probability Marklof. However, we are still far from the goal the 0.4r −s 3 an even there. For instance, an implication of the density e . GOE distribution Another chao>c billiard by Sinai. Z. Rudnik, 2008 Ω 0.7r otices of the AMS (0, 0) Ω 33 s=0 1 2 3 4 conjecture is that there should be arbitrarily large gaps in the spectrum. Can√you prove this for 4 rectangles with aspect ratio 5? The behavior of P (s) is governed by the statistics of the number N(λ, L) of levels in windows whose location λ is chosen at random, and whose length L is of the order of the mean spacing between levels. Statistics for larger windows also offer information about the classical dynamics and S the by Mar eve con gap rect T tics who Many-‐par>cle systems. Thermaliza>on through eigenstates. J. Von Neumann (1929), J. Deutch (1991), M. Srednicki (1994), M. Rigol et. al. (2008) Extension of Wigner ideas : Ergodic Hamiltonians within a Thouless energy shell looks like a random matrix. This shell contains Exponen>ally many levels. Hence recover Wigner-‐Dyson sta>s>cs, all eigenstates are sta>s>cally the same, so each one is a good microcanonical ensemble, … Eigen-‐func>ons are random vectors in a large-‐dimensional space. Observables (M. Srednicki 1996, M. Rigol et. al. 2008) Natural extension beyond the Thouless energy shell Figure 1 shows the level spacing distribution when the defect is placed on site 1 and on site ⌊L/2⌋. The first case corresponds to an integrable model and the distribution is a Poisson; the second case is a chaotic system, so the distribution is Wigner-Dyson. bases, the site- and mean-field basis. The site-basis is appropriate when analyzing the spatial delocalization of the system. To separate regular from chaotic behavior, a more appropriate basis consists of the eigenstates of the integrable limit of the model, which is known as the mean-field basis.27 In our case the integrable limit corresponds to Eqs. (1) with Jxy ̸= 0, ϵd ̸= 0, and Jz = 0. We start by writing the Hamiltonian in the site-basis. Interac>ng spin-‐chain with Let us denote these basis vectors by a |φ js⟩.ingle In theimpurity absence of the Ising interaction, the diagonalization of the Hamiltonian leadsand to Lthe mean-field (A. Gubin . Santos, 2012) basis vectors. They are 2 ! D given by |ξk ⟩ = j=1 bkj |φj ⟩. The diagonalization of the " L the # complete matrix, including Ising interaction, gives L ! ! ! zthe site-basis,z |ψi ⟩ = zD aij |φj ⟩. If theHeigenstates in ω S = ωS + ϵ (1b) = i i d Sdj=1 z i we use the relation between |φ ⟩ and |ξ ⟩, we may also j k i=1 i=1 write the L−1 eigenstates of the total Hamiltonian in Eqs. (1) ! $ basis % asx ' in the mean-field y y & z z HNN = Jxy⎛ Six Si+1 + ⎞Si Si+1 + Jz Si Si+1 . (1c) D D D " " i=1 " ∗ ⎠ ⎝ |ψi ⟩ = aij bkj |ξk ⟩ = cik |ξk ⟩. (8) Numerical checks atrices are pseudo-random vectors; that is, their ampli 20,21 des are random variables. All the eigenstates are FIG. 1: (Colorthey online) Levelthrough spacing distribution for the atistically similar, spread all basis vectors in and Eqs. are (1) with L = 15, 5 spins up, ω = 0, th noHamiltonian preferences therefore ergodic. ϵd = 0.5, Jxy = 1, and Jz = 0.5 (arbitrary units); bin size = Despite the success of random matrix theory in de0.1. (a) Defect on site d = 1;(b) defect on site d = 7. The ribingdashed spectral properties, lines statistical are the theoretical curves.it cannot capture e details of real quantum many-body systems. The fact j=1 to 1, L is the k=1 number of sites, We have set k=1 ! equal at random matrices are completely filled with statistix,y,z x,y,z Si Figures = σ2i shows /2 the are number the spin operatorscomponents at site i, and of principal llyOnset independent elements cimplies infinite-range interof B.quantum haos i s t he s ame a s o nset o f t hermaliza>on. x,y,z Number of principal components σfor the Pauli matrices. Hzingives i theare eigenstates in the site-basisThe [(a), term (b)] and the the tions and the simultaneous interaction of many partiZeeman splitting of each spin as determined by a static mean-field basis [(c), (d)] for thei, cases where the defect es. Real systems have few-body (most commonly only magnetic field the direction. sites[(b), are (d)]. assumed We now investigate how the transition(= from a Poissonmeasurement) is placed on sitein1 [(a), and Thermaliza>on: dephasing erange. nergy + Ez(c)] TH on siteAll⌊L/2⌋ o-body) interactions which are usually finite A to a Wigner-Dyson distribution affects the structure of to The levelthe of same delocalization increases significantly the site have energy splitting ω, except a insingle tter the picture of systems with finite-range interactions eigenstates. In particular, we study how delocalized d, chaotic to caused randomby matrices, whoseregime. energyHowever, splittingcontrary ω + ϵd is a magnetic provided by banded random matrices, which were also they are in both regimes. the largest values are restricted to the middle of the fieldini>al slightlyslarger than the field applied on specthe other Thermaliza>on: d ue t o E TH d elocaliza>on tates i n t he s pace o f 22 udied by off-diagonal ToWigner. determine Their the spreading of the elements eigenstatesare in aranpartrum, the states at the edges being more localized. This sites. This site is referred to as a defect. ticular basis, weindependent, look at theirbut components. Consider m eigenstates and statistically property israndom a consequence of the Gaussian of the (projec>on tare o enon-vanishing xponen>ally mAany vectors). (up)shape spin in the positive z direction is indicated % & |ψi ⟩ written thediagonal. basis vectors |ξkare ⟩ as density of states of systems with two-body interactions. by ly upantoeigenstate a fixed distance frominthe There 1 ! ↑⟩ or by theconcentration vector 0 ; aofspin the negative z direction |ψi ⟩ = ofDk=1random highest statesinappears in the middle cik |ξk ⟩. matrices It will be localized it has the par- |The %0& so ensembles that takeifinto account 2 (down) is represented ↓⟩ or mixing Anofup spincan on site of the spectrum, where by the |strong states ticipationtooffew few body basis vectors, that is, so if athat few |conly ik | make 12. 006), e restriction interactions, the (Basko, Parallels w ith m any-‐body l ocaliza>on A leiner, A ltshuler, D . leading +ω to widely distributed has energy a down eigenstates. spin has energy −ωi /2. significant contributions. will be delocalized if many ioccur i /2, and ements associated with thoseItinteractions are nonzero; 2 An interesting difference between the integrable and |cik | participate similar values. To quantify 23–25this criA spin up corresponds to an excitation. Huse et. 2with 008+ example is theal. two-body-random-ensemble (see chaotic regimes is the fluctuations of the number of prin- How robust are the eigenstates? Prepare the system in the energy eigenstate I A B Setup I: trace out few spins (do not touch them but no access to them) II A B Setup II: suddenly cutoff the link Same reduced density matrix at t=0 Define two relevant entropies (both are conserved in >me aQer quench): Entanglement (von Neumann’s entropy) Diagonal (measure of delocaliza>on), entropy of >me averaged density matrix aQer quench Both entropies are conserved in >me in both setups I A B II A B B>>A, trace out most of the system. Eigenstate is a typical state so expect that B<<A, trace out few spins, perhaps only one (say out of 1022). What happens? Remove one spin. Barely excite the system. Density matrix is almost diagonal (sta>onary)? Wrong (in nonintegrable case) Use ETH: Perform quench, deposit non extensive energy δE. Occupy all states in this energy shell. Cusng one spin is enough to recreate equilibrium (microcanonical) density matrix. (Numerical check L. Santos, M. Rigol, A.P. 2012 Sta>s>cal mechanics can be recovered from one postulate: All states within a narrow shell are equally occupied Thermodynamics (including this postulate) can be recovered from ETH plus dephasing (relaxa>on to the diagonal ensemble). Imagine the most integrable many-‐body system: collec>on of non-‐interac>ng Ising spins. The dynamics is very simple: each spin is conserved. A typical state with a fixed magne>za>on is thermal. Stat. Mech. works Quantum typicality: Typical many-‐body state of a big system (Universe) locally look like thermal (von Neumann 1929, Popescu et. al. 2006, Goldstein et. al. 2009) Flip 10 spins in the middle doing a Rabi pulse By performing a local quench we create a very atypical state, which is not thermal, whether the system is integrable or not. In an integrable system this state will never thermalize. Fundamental thermodynamic rela>on for open and closed systems Start from a sta>onary state. Consider some dynamical process Assume ini>al Gibbs Distribu>on Combine together Recover fundamental rela>on with the only assump>on of Gibbs distribu>on Imagine we are umping some energy into an isolated system. Does fundamental rela>on s>ll apply? Recover fundamental relation if the density matrix is not exponentially sparse. Density matrix is not sparse aQer any quench by local operators due to ETH. Example: hardcore bosons in 1D (with L. Santos and M. Rigol) ETH and delocaliza>on in the Hilbert space come together! Fluctua>on theorems (Bochkov, Kuzovlev, Jarzynski, Crooks) Ini>al sta>onary state + >me reversability: Eigenstate thermaliza>on hypothesis: microscopic probabili>es are smooth (independent on m,n) Bochkov, Kuzivlev, 1979, Crooks 1998 Integrate Crooks equality get Jarzynski equality, 1997 Jarzynski equality allows one to separate hea>ng from adiaba>c work for an arbitrary protocol. Hard to measure if work is large (e.g. extensive) Incremental hea>ng, do cumulant expansion Infinitesimal version of the second law + Einstein like rela>ons from ETH Open systems Two (or more conserved quan>>es): from ETH recover (non-‐ equilibrium) Onsager rela>ons Microcanonical ensemble + locality of interac>ons: recover sta>s>cal mechanics. ETH + dephasing: recover thermodynamics • Second law of thermodynamics (ETH is not needed) • Fundamental thermodynamic rela>on • Fluctua>on-‐dissipa>on rela>ons • Einstein rela>ons (and universal microwave hea>ng laws) • Fluctua>on theorems (Jarzynski, Crooks) • Onsager rela>ons • Detailed balance • Finite size correc>ons to temperature • Delocaliza>on in periodically driven (Floquet) systems. Divergence of the Magnus (Baker-‐Campbell-‐Hausdorff) expansion in the thermodynamic limit in ergodic systems (P. Ponte et. al. 2014) • Nontrivial long-‐range correla>ons in systems with flowing currents Integrable vs. Non-integrable systems Chaotic system: rapid (exponential) relaxation to microcanonical ensemble Integrable system: relax to constraint equilibrium: Quantum language: in both cases relax to the diagonal ensemble Integrable systems: generalized Gibbs ensemble (Jaynes 1957, Rigol 2007, J. Cardy, F. Essler, P. Calabrese, J.-S. Caux, E. Yuzbashyan …) . What if integrability is slightly broken? Relaxation to equilibrium in integrable, and nearly integrable systems. Prethermalization Fermi-Pasta-Ulam problem . . . . 1 2 3 n-2 n-1 n Slow variables Expectation: 1. Excite single normal mode 2. Follow dynamics of energies 3. Eventual energy equipartition Found: 1. 2. 3. 4. Quasiperiodic motion Energy localization in q-space Revivals of initial state No thermalization! Recent experiments on prethermaliza>on 1D condensates. Quantum Newton cradle. Kinoshita et. al. 2006 Prethermaliza>on of condensates on atom chips. Gring et. al. 2012 Transmission coefficient for pump-‐probe dynamics in VO2 oxide Image from J. Schmiedmayer page M. K. Liu, et al, Nature 487, 345 (2012) No equilibra>on between symmetric and an>-‐symmetric modes. Theory. • Original proposal by Berges et. al. (2004). Some of it is well known from long >me ( in semiconductor lasers) Pinned the term prethermaliza>on. PHYSICAL REVIEW LETTERS PRL 056403 (2009) to Kolmogorov • 103, Apparent connec>ons turbulence (V. Gurarie, 1994). 2 nkσ(t) [εk=0.5] nkσ(t) [εk=0.5] ∆n(t) d(t) d 0.25 0.2 a ponentially long time scales [18]. It U=0.5 b (“quench”). In this situation the time evolution for t ≥ • Possible understanding through r enormaliza>on g roup ( T. Gasenser, . Berges, L. RðtVÞ o (a) Falicov-Kimball model J(integrable) 0.08 (i) the envelope function U=8 0 is governed by a time-independent Hamiltonian Ĥ, but U=1 0.21 nonthermal Mathey, A.P., . Vosk, ofE. Ĥ. Altman, recent) the initial state at t A =. 0M is itra, not anReigenstate Rather …d med long-time limit decays to zero for t * 1=V, and ( the system is typicallyU=1.5 prepared in the ground0.1 state or a dth 0.06 value dstat differs from the therma thermal state of some other initial Hamiltonian Ĥ04. Re6 8 U • 0.17 Connec>on to qofuantum kine>c quantum equa>ons and G0.04 GE (S. Kehrein, M. Keigenbasis ollar, M. K jmi ¼ k j garding the behavior isolated interacting sys-U=6 U=2 ing an 0 m tems after a global quench, three main cases can be disP Eckstein,… r ecent). itVðk "k Þ m n hnjK jmi. I tinguished: (a) Integrable systems which relax to a non- U=5 þ m;n hjnihmji0 e U=2.5 28–44 0.13 0.02 thermal steady state, which often can be described U=4 oscillating dephase in th Quench to U=0.5 (fromeU=0, T=0.025) Fermi surface Gibbs discon>nuity for the the Gterms GE nsemble. by generalized ensembles (GGE) that take their U=3 U=3.3Explana>on through Long-time limit 1,2,34 large number of constants motion e into so that only energy-diagon M. Kollar 011 0 et al 2[13,15], interac>on quench. M. of Eckstein t al account; 2009 0 5 10 15 20 25 30 (b) 1nearly integrable systems that do not thermalize dithe sum. But from ½K ; D$ ¼ 0 it fo 0 rectly, but instead are trapped (b) Hubbard model (nearly integrable) U=0.5 in a prethermalized state d on intermediate timescales, which can be predicted from quantum number of jni so that hn 0.8 45–48 perturbation theory; U=1 and (c) nonintegrable systems relaxation towards prethermalization RðtVÞ vanishes in the time lim U=1.5 value 13,27,36,47,49 U=8 thermallong which thermalize directly. We review these plateau 0.6 cases in Sec. II. 0.01 accidental degeneracies between sec three U=6 Fig. 1 shows two U=2examples for the cases (a) and (b) for irrelevant). From Eq. (4) we theref U=5 simi0.4 the transient behavior is qualitatively rather which equals dstat for times 1=V ) t ) U lar. In particular, both the integrable and the nearly inU=4 U=2.5 2 2 0.2 tegrable system enter a long-lived nonthermal state. This of order OðV =U Þ. T=0) (ii) For the qu Quench to U=0.5 (from U=0, leads uscto the question whether and how the two cases 2 U=3.3 U=3 Long-time up to order U [Eq. (8)] obtain dlimit are0related and which properties they share. Our main 0 stat ¼ dð0Þ " "d, 0 2 4 6 8 claim0in this is 1 article 2 3 that4 (a) nonthermal 0 1steady states 2 3 t X Vij! in integrable systems and (b) prethermalized states in t t nearly integrable systems are in precise correspondence, "d ¼ " hcþ c ðn FIG. 1. Relaxation of the momentum occupation nkσ af-i! j! UL in the sense that both these nonthermal states are due ter an interaction quench from U = 0 to Uij! = 0.5 in (a) No general theore>cal framework yet, but a few ideas are very promising. so-called Zakharov-Kraichnan transformations. They More familiar examples of GGE: Kolmogorov turbulence factori integral. As a result one can (i) prove directly that Kolm reduce the collision integral to Images zero and (ii)W find that the Rayl from ikipedia Kolmogorov distributions are the only universal stationary p of kinetic equation. 3.1.1 Dimensional Estimations and Self-similarity An This section deals with universal flux distributions corresp stant fluxes of integrals of motion in the k-space. In this subs show that for scale-invariant media, these solutions may be A. N. Kolmogorov dimensional analysis (see also [3.1,2]). For complete self-similarity we shall first discuss the p universal flux distributions n(k) and the corresponding d−1 E(k) = (2k) ω(k)n(k). We shall recall how to find the for Pump energy at long wavelength. Dissipate at short wavelength. Non-‐equilibrium steady state trum E(k) for the turbulence of an incompressible fluid: in t Scaling solu>on of tonly he None avier Stokes equa>ons relevant parameter, the density ρ; and E(k) may b energy can the be tdimensions, hought of as the ρ, k and the energy flux P .This Comparing we o ∂v + (v∇)v = −∇p + ν △v ∇v = 0 E(k) ≃ P 2/3 k −5/3 ρ1/3 mode dependent temperature. A par>cular type of GGE. whichdis the famous Kolmogorov-Obukhov “5/3 law” [3.3,4] Zakharov, L’vov, Fal’kovich: erived this solu>on from the kine>c equa>ons Isotherm Potential applications to non-ergodic engines (work cycle 4 QL faster than thermalization time) B C Energy Energy Thermalization Thermalization Equilibrate with bath Equilibrate with bath Tq Tq Perform Work Perform Work FIG. 2: Comparison of Carnot engines and single-heat bath a hot reservoir that serves as a sourceengine of energy and a co Ergodic engine Non-ergodic regime, energy is injected into the engine. The gas within 0.8 mechanical work and then relaxes to back to its initial stat scales much slower than time scales on which work is perform 0.7 η Can much (ratiohave of injected energyhigher to initial efficiency. energy), ⇥ , for Carnot en c second law and 0.6 beat the e⇥ciency of a non-ergodic engine which acts as an effective o mt 0.5 Example: electric ηengines combustion engines. η3 vs. of three-dimensional ideal gas Lenoir engine, 5/3 . iency η D 0.4 η Reason for higher efficiency of non-‐ergodic engines. Need to release less entropy to the environment (P. Mehta and A.P., 2012). Ideal gas engine (Lenoir cycle) I) Deposit energy at constant volume II) Push piston until pressure drops to equilibrium III) Relax back to equilibrium at constant pressure If the energy is induced along the x-‐axis and the work cycle is shorter than the tehrmaliza>on >me get a higher efficiency. Closely related research: informa>on theory (Szilard engine), Informa>onal thermodynamics (realizing Maxwell’s daemons), informa>on and reversibility. Gauge transforma>ons in quantum systems Canonical transforma>ons = equa>ons of mo>on. Gauge poten>al = momentum operator Hamiltonian equa>ons of mo>on in a moving frame Special instantaneous frame, where U diagonalizes instantaneous Hamiltonian. This frame is convenient to study the non-‐adiaba>c response perturba>vely. General theory of non-‐adiaba>c response (with L. D’Alessio, 2013) Go to the interac>on (adiaba>c Heisenberg) picture with respect to . Use standard perturba>on theory Calculate expecta>on values of observables Expand the rate near t’=t. Simple expression which contains a lot Off-‐shell Berry curvature Mass tensor High-‐temperature (classical limit). Reduces to the equipar>>on theorem On-‐shell: F’ – asymmetric fric>on, Fric>on tensor Posi>ve temperature guarantees simultaneous posi>vity of η, κ (second law of thermodynamics) (Barankov, Levitov, Spivak; Yuzbashyan et. al.; Andreev, Gurarie, Radzihovsky; Chandran et. al., …) Need to solve coupled self-‐consistent equa>ons of mo>on. Adiaba>c limit: Born-‐Oppenheimer approxima>on. Berry (1989) – quantum correc>on to the Born-‐Oppenheimer force, given by the Fubini-‐Study metric. Our goal: go beyond adiaba>c approxima>on. The Hamiltonian H0 is just to build intui>on, e.g. Zero temperature + gap: recover macroscopic Hamiltonian (Newtonian) dynamics. Can always find a canonical momentum 1 1 ˙ equa>ons ˙ ⌫˙d(m ˙ µimplication. ~~)in tAt ~a)nd Hamiltonian These w=˙ithout issipa>on can b e )r˙ewriWen he L~agrangian L + ) + A ( V ( ) E ( (20) ~ ~ ⌫µ µ µ 0 tion (19) has another interesting zero temperature (m + ) + A ( ) V ( E ( ) (20) ⌫ ⌫µ µ2 µ µ 0 form 2 At zero temperature 0 ion. ipative tensors (⌘ and F ) vanish (unless the system is tuned to a ~ ) = h0 ~ )|0 i the system tuned to a low-dimensional reproduces Eq. (19) where Aµ (i~ and ) = h0 |A |0 ih0and E~0)|0 ([26]). |H( ~ ~ µexcitations oint or if itAis has gapless In this 19) where ( ) = h0 |A |0 E ( ) = |H( i µ µ 0 excitations [26]). In this are Berry the of the as Berry connection equations and Hamiltonian (5)) in the (19) can value beconnection viewed a Lagrangian fact, it inthe and Hamiltonian (see (5))ofinmotion. the(see in- If of motion. If fact, it ground state and we have used (see Eq. (16)): stantaneous (~Lagrangian: -dependent) otions see that the ependent) ground state and we have used (see Eq. (16)): ! ! @Aµ @A 1⌫ ˙ = i [@⌫ h0 |@µ 0˙ i @˙ µ h0 |@! ! 0 i] = ih0 | @ @ @ i = F⌫µ . ~⌫@) V@ (~@) |0E⌫i0 (= ~µ)F .µ @ ⌫ |0(20) L = (m + ) + A ( @⌫(h0 |@ 0 i @ h0 |@ 0 i] = ih0 | @ ⌫ ⌫µ µ µ µ ~ ~ @ ) ⌫ µE@02(µ ) µ ⌫ µ µ ⌫ ⌫µ ⌫(20) From the Lagrangian (20) we can define the canonical conjugate ~ )the ~ ) =momenta ~ )|0 es Eq. (19) where A ( = h0 |A |0 i and E ( h0 |H( i ~ ~ ngian (20) we can define canonical momenta conjugate µ µ 0 ndto Ethe ) = h0 |H( )|0 i -‐ responsible for the Casimir force 0 ( coordinates : ⌫ es alue⌫ :of(see the(5)) Berry connection and Hamiltonian (see (5)) in the inonian in the in@L ous used (~ -dependent) ground and we have (see ave (see Eq. (16)): ˙ µ used ~ ) Eq. (16)): (21) p⌫ ⌘ state = (m + ) + A ( @L ⌫µ ⌫µ ⌫ p⌫ ⌘ = (m⌫µ + ⌫µ )˙ ⌫˙ µ + A⌫ (~ ) (21) @ ˙ @! ! ! A⌫ ! ⌫ @ and @ µithe i = F . [@@⌫emergent h0 0 i @ h0 |@ 0 i] = ih0 | @ @ @ ⌫= µ @|@ ⌫ |0 ⌫µ ⌫ µ µ @ ⌫ |0 i = F⌫µ . µ µ ⌫ Hamiltonian: tµHamiltonian: 1 1 ˙ nical momenta conjugate H ⌘ p L = A⌫ )(mthe + )canonical Aµmomenta ) + V (~ ) +conjugate E0 (~ ). (22) e Lagrangian can 1 ⌫ ⌫ (20) we (p ⌫1 define ⌫µ~(pµ 2 ⌫µ (pµ Aµ ) + V ( ) + E0 (~ ). (22) L = (p⌫ A⌫ )(m + ) ordinates 2 ⌫: Clearly the Berry connection term plays the role of the vector potential. Thus yAconnection plays the role of of the vector potential. H amiltonian dynamics w ith mHamiltonian inimal c~oupling tThus o the gauge fields. @L (21) (~Emergent )see that term we the whole formalism the dynamics for arbitrary ⌫ ˙ p⌫ass ⌘rof =Hamiltonian (m⌫µ +term: ⌫µ )dynamics A⌫ (1989 ) arbitrary (21) µ. + whole formalism the for Without m enormaliza>on M B erry ˙ macroscopic degrees @ ⌫ of freedom is actually emergent. Without mass renorrees of freedom is actually emergent. Without mass renor- Example: par>cle in a box Massless membrane. What mass will we measure? Mass of two walls is not equal to the sum of masses of each wall measured separately!. Mass of photons coming. Mass renormaliza>on near a quantum cri>cal point Mass has a singularity near QCP. Scaling dimension of the mass density Mass diverges for Below cri>cal dimension it can be hard to pass through QCP From a snowball to infla>on in cosmology (hypothe>cal scenario) Scalar field rolls affec>ng the Higgs mass. Near QCP (zero Higgs mass) it gets very heavy and dynamically localizes. The Kibble-‐Zurek type scaling argument Scaling dimension of velocity Divergent KZ correla>on length Characteris>c gap Energy (heat) density Ini>al kine>c energy Can expect localiza>on if Localiza>on from the Kibble-‐Zurek Localiza>on is expected if we absorb more energy than it has The slower the system goes the more likely it is localized Same criterion for the localiza>on as from the mass divergence. Not really surprising from understanding the scaling theory. Check numerically. Transverse field Ising model First subtract the GS energy so that the field moves in a flat poten>al (later revise this assump>on). Trapping condi>on Expect trapping when Observe sharp transi>on to the trapping regime at 0.1 0.0 0.1 0.2 0.1 0.3 0.4 0.5 0 0.01 1 2 1 10 3 4 5 Finite slope Start from the rest at some and release the system. What will happen? Naïve answer: will roll down, perhaps stumble a bit near QCP and move on. Wrong! The system can be truly self-‐trapped due to hea>ng Expect two scenarios: Untrapped (adiaba>c) Trapped (enough hea>ng) Start far from QCP: not too fast Start near QCP : not too slow Expect trapping when Trapping is possible only if Numerical phase diagram Numerical constants are not very small, but this is quite typical. Interes>ng non-‐equilibrium dynamics if start near QCP. Bare mass is irrelevant and can be set to zero. 5 100 µ =1, 80 60 µ =10, =0.0001 =0.0001 µ =1, =0.0003 µ =1, =0.0010 µ =1, =0.0030 40 20 0 0.00 (c) 0.05 0.10 Sc a le d tim e 0.15 Except for transients and long >mes have a full scaling collapse 0.20 Outlook: dynamic trapping is consistent with thermodynamic trapping Consider a fixed energy state. Equilibrium: maximize entropy The entropy is maximized near QCP where excita>ons are cheapest. From scaling expect entropy maximum near QCP for finite range of slopes. Typical phase diagram of cuprates Image: D. M. Broun, Nature Phys. (2008) QCP is a natural place for localizing a macroscopic DOF like an order parameter. Similar to the order by disorder scenario. Summary • ETH -‐> thermodynamics • Relaxa>on in weakly nonintegrable systems through prethermaliza>on • Recover macroscopic Hamiltonian dynamics from >me scale separa>on • Divergence of mass near cri>cal points. Dynamical self-‐ trapping near quantum cri>cal points. F. Essler, talk at KITP, 2012 5. Generalized Gibbs Ensemble a par>cular (transverse field Ising) mof odel IProve local (in space) integrals motion [Im, In]=[I m befor Works both for equal and non-‐equal >me correla>on func>ons. Need only integrals of mo>on, which “fit” to the subsystem our case In = X j In (j, j + 1, . . . , j + n) If we can not measure In – have too many fisng parameters. What if integrability is slightly broken?