Download Quantum non-‐equilbrium dynamics in closed systems. - Indico

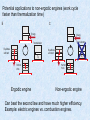
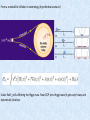
Quantum non-­‐equilbrium dynamics in closed systems. Anatoli Polkovnikov, BU Par>al list of recent collaborators L. D’Alessio Y. Kafri A. Katz M. Kolodrubetz
P. Mehta M. Rigol L. Santos BU, PennState Technion BU BU BU PennState Yeshiva Non-­‐equilibrium phenomena in CM and ST, ICTP, Trieste, 07/03/2014 Brief Outline •  ETH and thermodynamics •  Relaxa>on in integrable and weakly non-­‐integrable systems •  Emergence of macroscopic Hamiltonian dynamics from non-­‐adiaba>c response •  Extension of Kibble-­‐Zurek mechanism to dynamical fields. Dynamical localiza>on transi>on near quantum cri>cal points. •  Floquet systems Non-­‐equilibrium quantum systems J. Von Neumann: Non-­‐equilibrium theory is a “theory of non-­‐elephants”. •  Chaos and thermaliza>on in classical and quantum isolated systems, mostly aQer sudden quenches •  Relaxa>on in weakly interac>ng systems. Prethermaliza>on and the generalized Gibbs ensemble. •  Steady states: phases and phase transi>ons in driven systems (isolated or dissipa>ve) •  Many-­‐body localiza>on: interplay of disorder and ergodicity •  Universal non-­‐equilibrium dynamics. •  Dynamical phase transi>ons (in >me). •  Many more: non-­‐equilibrium Stat. Mech., biological systems, ac>ve maWer,
… Classical chao>c systems 3
chaos implies strong usually exponential sensitivity of the trajectories to small perturbations. In
Regular vs. chao>c mo>on: like beauty. When we see it we recognize it. 3
chaos implies strong usually exponential sensitivity of the trajectories to small perturbations. In
No mathema>cally rigorous defini>on of chaos. Standard prac>cal defini>on: Divergent trajectories. FIG. 1 Examples of trajectories of a particle bouncing in a cavity (i) non-chaotic circular (top left image)
The analysis of
with φ = π is even simpler
Kthe other attractor
K2
!
λ1,2 = 1 +
± K+
.
(I.15)
2
4
K
K2
λ1,2 = 1 +
± K+
.
2
4
early for any positive K there are two real solutions with one larger than one. So this point is
Clearly for any positive K there are two real solutions with one larger than one. So this p
No chaos in one-­‐dimension. ways unstable. This is not very surprising since this attractor corresponds to the situation, where
always unstable. This
is not very
surprising
since this
to the situation,
unique rela>on aattractor
nd xfast
. corresponds
mass sits on top of the potential. It isEnsures interesting
that if instead
of bδetween kicks onepapplies
periodic
a mass sits on top of the potential. It is interesting that if instead of δ kicks one applies fast p
otion of the pendulum: K = K0 + a sin(νt) then one can stabilize the top equilibrium φ = π.
motion of the pendulum: K = K0 + a sin(νt) then one can stabilize the top equilibrium
his is known as the Kapitza effect (or Kapitza pendulum) and there are many demonstrations
This is known as the Kapitza effect (or Kapitza pendulum) and there are many demonst
w it works. In Fig. 2 we show the phase space portrait of the kicked rotor at different values of
how it works. In Fig. 2 we show the phase space portrait of the kicked rotor at different va
. It is clear that as K increases the system becomes more and more chaotic. At K = Kc ≈ 1.2
K. It is clear that as K increases the system becomes more and more chaotic. At K = Kc
ere is a delocalization transition, where the chaotic region becomes delocalized and the system
there is a delocalization transition, where the chaotic region becomes delocalized and the
creases its energy without bound.
increases its energy without bound.
Simplest chao>c system – kicked rotor (kicked Josephson junc>on). Break energy conserva>on by kicks. Equa>ons of mo>on: Chirikov standard map Transition from regular (localized) to chaotic
Transition from regular (localized) to chaotic
(delocalized) motion as K increases. Chirikov,
(delocalized) motion as K increases. Chirikov,
1971
1971
K=0.5
K=0.5
K=K
g=0.971635
K=Kg=0.971635
K=5
(images taken
from
scholarpedia.org)
K=5
(images taken
from
scholarpedia.org)
Quantum systems. Linear equa>ons of mo>on no chaos? Linear equa>ons of mo>on like harmonic chains are non-­‐chao>c. Any solu>on is a superposi>on of normal modes (eigenstates). von Neumann (1929): chaos (and ergodicity) are encoded in observables. 13
Wigner (1955), thinking about spectrum of complex nuclei: Hamiltonians of the nuclei are essen>ally like random matrices. ese
levels
in thisis interval
(e.g.
over it. many nearby
Any ini>al structure rapidly lost o
nce we averaged
start diagonalizing predic>on: level repulsion. Wigner-­‐Dyson sta>s>cs (Wigner SIn
urmize) ryFamous different
from
the
Wigner
- Dyson
statistics.
particular,
miltonian is completely diagonal in the single-particle basis.
interval
δE = ω there are no levels is simply expressed by
Non-­‐chao>c “generic systems”. Expect Poisson sta>s>cs (Berry-­‐Tabor conjecture, 1977) P0 (ω) = exp[−ω],
(II.10)
Surmize
(II.7).some
This statement
in fact known in literature
gure
gives
idea ofis how
behave like a sequence of independent random variables (i.e. have Poisson statistics)
hat the underlying classical dynamics is completely integrable. In Fig. 5 we show level
Examples of level sta>s>cs 15
y = e−s
FIG. 7 Sinai billiard, which is a classical chaotic systems, similar to the Bunimovich stadium considered
arlier. Left panel illustrates the Billiard and the classical trajectory (image source Wikipedia). Right
anel shows level spacing statistics for the same billiard together with the Poisson and the Wigner-Dyson
istributions (image source O. Bohigas, M.J. Giannoni,
C.7Schmit
Phys. which
Rev. Lett.
52, 1 chaotic
(1984)).systems, similar to the Bunimovich stadium considered
FIG.
Sinai billiard,
is a classical
s=0
1
2
3
4
earlier. Left panel illustrates the Billiard and the classical trajectory (image source Wikipedia). Righ
the Wigner-Dyson
statistics.
Incommensurate 2D box. Sinai Billiard. O. for
Bohigas et. atogether
l. 1984 statistics
the same billiard
with the Poisson and the Wigner-Dyson
of eigenvalues π (m /a + n /b ) of a
Notices
the AMS
55, 32 (2008)). The levels are given by a simple
formula: E (image
=
distributions
sourcechaotic
O. Bohigas,
M.J. also
Giannoni,
C. Schmit Phys. Rev. Lett. 52, 1 (1984)).
Z. R
2another
008 nhaos?,
Fig.
8udnik, weof show
example
of the level statistics
for a classical
system
analyzed
rectangle
with
sufficiently
incommensurable
√
nergy
levels
in
classical
chaotic ratio
systems
are
typically
well
described
by
Figure
It is
conjectured
the
distribution
panel
shows
level
el statistics
in 3.
a rectangular
cavity with thethat
of sides
a/b = 4 5 (Z.
Rudnick,
What
Is spacing
2
2
2
2
2
n,m
n2 /b2 ).
sides a, b is that of a Poisson process. The
mean is 4π /ab by simple geometric reasoning,
energy levels√in classical chaotic systems are typically well described by the Wigner-Dyson statistics
or a in
rectangular
cavity with
a and asymptotic
b, which have the
following ratio: a/b = 4 5.
ties in the spectrum, P (s) collapses to a point
conformity
withsides
Weyl’s
formula.
massfor
at the
origin. Deviations
are also
seen in the
In
Fig.
8
we
show
another
example
of
the
level
statistics
a classical
chaotic
system
also analyzed
Here
are plotted
the
statistics
ofYet
the
y agree
perfectly
well with the
Poisson
statistics.
thegaps
Berry-Tabor conjecture is not
chaotic case in arithmetic examples. Nonetheless,
(1, 1)
empirical studies offer tantalizing evidence for
λi+1 − λi found for rthe first 250,000
the “generic” truth of the conjectures, as Figures
0.4
3 and 4 show.
eigenvalues
of a rectangle with side/bottom
ties
√
GOE
distribution
Some progress on the Berry-Tabor conjecture in
4
ma
ratio 5 and area 4π , binned
into
intervals
of
the case of the rectangle billiard has been achieved
r
cha
0.7
(1, 1)
by
Sarnak,
by
Eskin,
Margulis,
and
Mozes,
and
by
emp
0.1, compared to the expected probability
Marklof. However, we are still far from the goal
the
0.4r
−s
3 an
even there. For instance, an implication of the
density e .
GOE distribution
Another chao>c billiard by Sinai. Z. Rudnik, 2008 Ω
0.7r
otices of the AMS
(0, 0)
Ω
33
s=0
1
2
3
4
conjecture is that there should be arbitrarily large
gaps in the spectrum. Can√you prove this for
4
rectangles with aspect ratio 5?
The behavior of P (s) is governed by the statistics of the number N(λ, L) of levels in windows
whose location λ is chosen at random, and whose
length L is of the order of the mean spacing
between levels. Statistics for larger windows also
offer information about the classical dynamics and
S
the
by
Mar
eve
con
gap
rect
T
tics
who
Many-­‐par>cle systems. Thermaliza>on through eigenstates. J. Von Neumann (1929), J. Deutch (1991), M. Srednicki (1994), M. Rigol et. al. (2008) Extension of Wigner ideas : Ergodic Hamiltonians within a Thouless energy shell looks like a random matrix. This shell contains Exponen>ally many levels. Hence recover Wigner-­‐Dyson sta>s>cs, all eigenstates are sta>s>cally the same, so each one is a good microcanonical ensemble, … Eigen-­‐func>ons are random vectors in a large-­‐dimensional space. Observables (M. Srednicki 1996, M. Rigol et. al. 2008) Natural extension beyond the Thouless energy shell Figure 1 shows the level spacing distribution when the
defect is placed on site 1 and on site ⌊L/2⌋. The first case
corresponds to an integrable model and the distribution
is a Poisson; the second case is a chaotic system, so the
distribution is Wigner-Dyson.
bases, the site- and mean-field basis. The site-basis is
appropriate when analyzing the spatial delocalization of
the system. To separate regular from chaotic behavior,
a more appropriate basis consists of the eigenstates of
the integrable limit of the model, which is known as the
mean-field basis.27 In our case the integrable limit corresponds to Eqs. (1) with Jxy ̸= 0, ϵd ̸= 0, and Jz = 0.
We start by writing the Hamiltonian in the site-basis.
Interac>ng spin-­‐chain with Let
us denote these
basis vectors
by a
|φ js⟩.ingle In theimpurity absence
of the Ising interaction, the diagonalization of the Hamiltonian
leadsand to Lthe
mean-field
(A. Gubin . Santos, 2012) basis vectors. They are
2
!
D
given by |ξk ⟩ = j=1 bkj |φj ⟩. The diagonalization of the
" L the #
complete matrix,
including
Ising interaction, gives
L
!
!
!
zthe site-basis,z |ψi ⟩ = zD aij |φj ⟩. If
theHeigenstates
in
ω
S
=
ωS
+
ϵ
(1b)
=
i i
d Sdj=1
z
i
we use the
relation
between
|φ
⟩
and
|ξ
⟩,
we
may
also
j
k
i=1
i=1
write the L−1
eigenstates of the total Hamiltonian in Eqs. (1)
! $ basis
% asx
'
in the mean-field
y y &
z z
HNN =
Jxy⎛ Six Si+1
+
⎞Si Si+1 + Jz Si Si+1 . (1c)
D
D
D
"
"
i=1 "
∗ ⎠
⎝
|ψi ⟩ =
aij bkj |ξk ⟩ =
cik |ξk ⟩.
(8)
Numerical checks atrices are pseudo-random vectors; that is, their ampli
20,21
des are random variables.
All the eigenstates are
FIG. 1:
(Colorthey
online)
Levelthrough
spacing distribution
for the
atistically
similar,
spread
all basis vectors
in and
Eqs. are
(1) with
L = 15,
5 spins up, ω = 0,
th noHamiltonian
preferences
therefore
ergodic.
ϵd = 0.5, Jxy = 1, and Jz = 0.5 (arbitrary units); bin size =
Despite
the success of random matrix theory in de0.1. (a) Defect on site d = 1;(b) defect on site d = 7. The
ribingdashed
spectral
properties,
lines statistical
are the theoretical
curves.it cannot capture
e details of real quantum many-body systems. The fact
j=1 to 1, L is the
k=1 number of sites,
We have set k=1
! equal
at random matrices are completely filled with statistix,y,z
x,y,z
Si Figures
= σ2i shows
/2 the
are number
the spin
operatorscomponents
at site i, and
of principal
llyOnset independent
elements cimplies
infinite-range
interof B.quantum haos i
s t
he s
ame a
s o
nset o
f t
hermaliza>on. x,y,z
Number of principal components
σfor
the Pauli
matrices.
Hzingives
i theare
eigenstates
in the
site-basisThe
[(a), term
(b)] and
the the
tions and the simultaneous interaction of many partiZeeman
splitting
of each
spin
as determined
by a static
mean-field
basis [(c),
(d)] for
thei, cases
where the defect
es. Real systems have few-body (most commonly only
magnetic
field
the
direction.
sites[(b),
are (d)].
assumed
We now investigate how
the transition(= from
a Poissonmeasurement) is placed on
sitein1 [(a),
and
Thermaliza>on: dephasing erange.
nergy + Ez(c)]
TH on siteAll⌊L/2⌋
o-body)
interactions
which
are
usually
finite
A
to a Wigner-Dyson distribution affects the structure of to
The
levelthe
of same
delocalization
increases significantly
the site
have
energy splitting
ω, except a insingle
tter the
picture
of
systems
with
finite-range
interactions
eigenstates. In particular, we study how delocalized d,
chaotic
to caused
randomby
matrices,
whoseregime.
energyHowever,
splittingcontrary
ω + ϵd is
a magnetic
provided
by banded
random matrices, which were also
they
are
in
both
regimes.
the
largest
values
are
restricted
to
the
middle
of
the
fieldini>al slightlyslarger
than
the
field
applied
on specthe other
Thermaliza>on: d
ue t
o E
TH d
elocaliza>on tates i
n t
he s
pace o
f 22
udied by
off-diagonal
ToWigner.
determine Their
the spreading
of the elements
eigenstatesare
in aranpartrum,
the
states
at
the
edges
being
more
localized.
This
sites. This site is referred to as a defect.
ticular
basis, weindependent,
look at theirbut
components.
Consider
m eigenstates and
statistically
property
israndom a consequence
of the Gaussian
of the
(projec>on tare
o enon-vanishing
xponen>ally mAany vectors). (up)shape
spin
in
the
positive
z
direction
is
indicated
%
&
|ψi ⟩ written
thediagonal.
basis vectors
|ξkare
⟩ as
density of states of systems
with two-body interactions. by
ly upantoeigenstate
a fixed
distance
frominthe
There
1
!
↑⟩ or
by theconcentration
vector 0 ; aofspin
the negative
z direction
|ψi ⟩ = ofDk=1random
highest
statesinappears
in the middle
cik |ξk ⟩. matrices
It will be localized
it has
the par- |The
%0&
so ensembles
that takeifinto
account
2
(down)
is represented
↓⟩ or mixing
Anofup
spincan
on site
of the spectrum,
where by
the |strong
states
ticipationtooffew
few body
basis vectors,
that is, so
if athat
few |conly
ik | make
12. 006), e restriction
interactions,
the (Basko, Parallels w
ith m
any-­‐body l
ocaliza>on A
leiner, A
ltshuler, D
. leading +ω
to widely
distributed
has energy
a down eigenstates.
spin has energy −ωi /2.
significant
contributions.
will be delocalized
if many ioccur
i /2, and
ements
associated
with thoseItinteractions
are nonzero;
2
An interesting
difference
between
the integrable and
|cik | participate
similar values. To quantify
23–25this criA spin
up corresponds
to an
excitation.
Huse et. 2with
008+ example
is
theal. two-body-random-ensemble
(see
chaotic regimes is the fluctuations of the number of prin-
How robust are the eigenstates? Prepare the system in the energy eigenstate I A B Setup I: trace out few spins (do not touch them but no access to them) II A B Setup II: suddenly cutoff the link Same reduced density matrix at t=0 Define two relevant entropies (both are conserved in >me aQer quench): Entanglement (von Neumann’s entropy) Diagonal (measure of delocaliza>on), entropy of >me averaged density matrix aQer quench Both entropies are conserved in >me in both setups I A B II A B B>>A, trace out most of the system. Eigenstate is a typical state so expect that B<<A, trace out few spins, perhaps only one (say out of 1022). What happens? Remove one spin. Barely excite the system. Density matrix is almost diagonal (sta>onary)? Wrong (in nonintegrable case) Use ETH: Perform quench, deposit non extensive energy δE. Occupy all states in this energy shell. Cusng one spin is enough to recreate equilibrium (microcanonical) density matrix. (Numerical check L. Santos, M. Rigol, A.P. 2012 Sta>s>cal mechanics can be recovered from one postulate: All states within a narrow shell are equally occupied Thermodynamics (including this postulate) can be recovered from ETH plus dephasing (relaxa>on to the diagonal ensemble). Imagine the most integrable many-­‐body system: collec>on of non-­‐interac>ng Ising spins. The dynamics is very simple: each spin is conserved. A typical state with a fixed magne>za>on is thermal. Stat. Mech. works Quantum typicality: Typical many-­‐body state of a big system (Universe) locally look like thermal (von Neumann 1929, Popescu et. al. 2006, Goldstein et. al. 2009) Flip 10 spins in the middle doing a Rabi pulse By performing a local quench we create a very atypical state, which is not thermal, whether the system is integrable or not. In an integrable system this state will never thermalize. Fundamental thermodynamic rela>on for open and closed systems Start from a sta>onary state. Consider some dynamical process Assume ini>al Gibbs Distribu>on Combine together Recover fundamental rela>on with the only assump>on of Gibbs distribu>on Imagine we are umping some energy into an isolated system. Does fundamental rela>on s>ll apply? Recover fundamental relation if the density matrix is not exponentially
sparse.
Density matrix is not sparse aQer any quench by local operators due to ETH. Example: hardcore bosons in 1D (with L. Santos and M. Rigol)
ETH and delocaliza>on in the Hilbert space come together! Fluctua>on theorems (Bochkov, Kuzovlev, Jarzynski, Crooks) Ini>al sta>onary state + >me reversability: Eigenstate thermaliza>on hypothesis: microscopic probabili>es are smooth (independent on m,n) Bochkov, Kuzivlev, 1979, Crooks 1998 Integrate Crooks equality get Jarzynski equality, 1997 Jarzynski equality allows one to separate hea>ng from adiaba>c work for an arbitrary protocol. Hard to measure if work is large (e.g. extensive) Incremental hea>ng, do cumulant expansion Infinitesimal version of the second law + Einstein like rela>ons from ETH Open systems Two (or more conserved quan>>es): from ETH recover (non-­‐
equilibrium) Onsager rela>ons Microcanonical ensemble + locality of interac>ons: recover sta>s>cal mechanics. ETH + dephasing: recover thermodynamics •  Second law of thermodynamics (ETH is not needed) •  Fundamental thermodynamic rela>on •  Fluctua>on-­‐dissipa>on rela>ons •  Einstein rela>ons (and universal microwave hea>ng laws) •  Fluctua>on theorems (Jarzynski, Crooks) •  Onsager rela>ons •  Detailed balance •  Finite size correc>ons to temperature •  Delocaliza>on in periodically driven (Floquet) systems. Divergence of the Magnus (Baker-­‐Campbell-­‐Hausdorff) expansion in the thermodynamic limit in ergodic systems (P. Ponte et. al. 2014) •  Nontrivial long-­‐range correla>ons in systems with flowing currents Integrable vs. Non-integrable systems
Chaotic system: rapid
(exponential) relaxation to
microcanonical ensemble
Integrable system: relax to
constraint equilibrium:
Quantum language: in both cases relax to the diagonal ensemble
Integrable systems: generalized Gibbs ensemble (Jaynes 1957, Rigol 2007, J.
Cardy, F. Essler, P. Calabrese, J.-S. Caux, E. Yuzbashyan …) . What if integrability is
slightly broken?
Relaxation to equilibrium in integrable, and nearly integrable
systems. Prethermalization
Fermi-Pasta-Ulam problem
. . . .
1
2
3
n-2 n-1
n
Slow variables
Expectation:
1.  Excite single normal mode
2.  Follow dynamics of
energies
3.  Eventual energy
equipartition
Found:
1. 
2. 
3. 
4. 
Quasiperiodic motion
Energy localization in q-space
Revivals of initial state
No thermalization!
Recent experiments on prethermaliza>on 1D condensates. Quantum Newton cradle. Kinoshita et. al. 2006 Prethermaliza>on of condensates on atom chips. Gring et. al. 2012 Transmission coefficient for pump-­‐probe dynamics in VO2 oxide Image from J. Schmiedmayer page M. K. Liu, et al, Nature 487, 345 (2012)
No equilibra>on between symmetric and an>-­‐symmetric modes. Theory. •  Original proposal by Berges et. al. (2004). Some of it is well known from long >me ( in semiconductor lasers) Pinned the term prethermaliza>on. PHYSICAL REVIEW LETTERS
PRL
056403
(2009) to Kolmogorov •  103,
Apparent connec>ons turbulence (V. Gurarie, 1994). 2
nkσ(t) [εk=0.5]
nkσ(t) [εk=0.5]
∆n(t)
d(t)
d
0.25
0.2
a
ponentially long time scales [18]. It
U=0.5
b
(“quench”). In this situation the time evolution for t ≥
•  Possible understanding through r
enormaliza>on g
roup (
T. Gasenser, . Berges, L. RðtVÞ o
(a) Falicov-Kimball
model J(integrable)
0.08
(i)
the
envelope
function
U=8
0 is governed by a time-independent
Hamiltonian
Ĥ,
but
U=1
0.21
nonthermal
Mathey, A.P., . Vosk, ofE. Ĥ.
Altman, recent) the
initial state
at t A
=. 0M
is itra, not anReigenstate
Rather …d med
long-time
limit
decays
to
zero
for
t
* 1=V,
and (
the system is typicallyU=1.5
prepared in the ground0.1
state or a dth 0.06
value dstat differs from the therma
thermal state of some other initial Hamiltonian Ĥ04. Re6
8 U
•  0.17
Connec>on to qofuantum kine>c quantum
equa>ons and G0.04
GE (S. Kehrein, M. Keigenbasis
ollar, M. K jmi ¼ k j
garding
the behavior
isolated interacting
sys-U=6
U=2
ing
an
0
m
tems after a global quench, three main cases can be disP
Eckstein,… r
ecent). itVðk
"k
Þ
m
n hnjK jmi. I
tinguished: (a) Integrable
systems which relax to a non- U=5
þ
m;n hjnihmji0 e
U=2.5
28–44
0.13
0.02
thermal steady state,
which often can be described
U=4
oscillating
dephase
in th
Quench to
U=0.5
(fromeU=0,
T=0.025)
Fermi surface Gibbs
discon>nuity for the the Gterms
GE nsemble. by generalized
ensembles (GGE)
that take their
U=3
U=3.3Explana>on through Long-time limit
1,2,34
large number
of constants
motion e
into
so that only energy-diagon
M. Kollar 011 0 et al 2[13,15],
interac>on quench. M. of
Eckstein t al account;
2009 0
5
10
15
20
25
30
(b) 1nearly integrable systems that do not thermalize dithe
sum.
But
from
½K
;
D$
¼
0 it fo
0
rectly, but instead are trapped
(b) Hubbard model (nearly integrable)
U=0.5 in a prethermalized state
d
on intermediate timescales, which can be predicted from
quantum number of jni so that hn
0.8
45–48
perturbation theory; U=1
and (c) nonintegrable systems
relaxation towards
prethermalization
RðtVÞ
vanishes
in
the
time lim
U=1.5
value
13,27,36,47,49 U=8
thermallong
which thermalize directly.
We review these
plateau
0.6 cases in Sec. II.
0.01
accidental degeneracies between sec
three
U=6
Fig. 1 shows two
U=2examples for the cases (a) and (b) for
irrelevant). From Eq. (4) we theref
U=5 simi0.4 the transient behavior is qualitatively rather
which
equals dstat for times 1=V ) t ) U
lar. In particular, both the integrable and the nearly inU=4
U=2.5
2
2
0.2
tegrable
system enter a long-lived nonthermal state. This
of
order
OðV
=U
Þ. T=0)
(ii) For the qu
Quench
to
U=0.5
(from
U=0,
leads uscto the question
whether
and
how
the
two
cases
2
U=3.3
U=3
Long-time
up to order U [Eq. (8)]
obtain
dlimit
are0related and which properties they share. Our main
0
stat ¼ dð0Þ " "d,
0
2
4
6
8
claim0in this
is
1 article
2
3 that4 (a) nonthermal
0
1steady states
2
3
t
X Vij!
in integrable systems
and (b) prethermalized states
in
t
t
nearly integrable systems are in precise correspondence,
"d ¼ "
hcþ c ðn
FIG. 1. Relaxation of the momentum occupation nkσ af-i! j!
UL
in the sense that both these nonthermal states are due
ter an interaction quench from U = 0 to Uij!
= 0.5 in (a)
No general theore>cal framework yet, but a few ideas are very promising. so-called
Zakharov-Kraichnan
transformations.
They
More familiar examples of GGE: Kolmogorov turbulence factori
integral. As a result one can (i) prove directly that Kolm
reduce the collision integral to Images zero and
(ii)W
find
that the Rayl
from ikipedia Kolmogorov distributions are the only universal stationary p
of kinetic equation.
3.1.1 Dimensional Estimations and Self-similarity An
This section deals with universal flux distributions corresp
stant fluxes of integrals of motion in the k-space. In this subs
show that for scale-invariant media, these solutions may be
A. N. Kolmogorov dimensional analysis (see also [3.1,2]).
For complete self-similarity we shall first discuss the p
universal flux distributions n(k) and the corresponding
d−1
E(k)
=
(2k)
ω(k)n(k). We shall recall how to find the for
Pump energy at long wavelength. Dissipate at short wavelength. Non-­‐equilibrium steady state trum E(k) for the turbulence of an incompressible fluid: in t
Scaling solu>on of tonly
he None
avier Stokes equa>ons relevant
parameter,
the density ρ; and E(k) may b
energy can the
be tdimensions,
hought of as the ρ, k and the energy flux P .This Comparing
we o
∂v + (v∇)v = −∇p + ν △v ∇v = 0 E(k) ≃ P 2/3 k −5/3 ρ1/3
mode dependent temperature. A par>cular type of GGE. whichdis
the famous
Kolmogorov-Obukhov
“5/3 law” [3.3,4]
Zakharov, L’vov, Fal’kovich: erived this solu>on from the kine>c equa>ons Isotherm
Potential applications to non-ergodic engines (work cycle
4
QL
faster than thermalization time)
B
C
Energy
Energy
Thermalization
Thermalization
Equilibrate
with bath
Equilibrate
with bath
Tq
Tq
Perform
Work
Perform
Work
FIG. 2: Comparison of Carnot engines and single-heat bath
a hot reservoir that
serves as a sourceengine
of energy and a co
Ergodic engine
Non-ergodic
regime, energy is injected into the engine. The gas within
0.8
mechanical work and then relaxes to back to its initial stat
scales much slower than time scales on which work is perform
0.7
η
Can
much
(ratiohave
of injected
energyhigher
to initial efficiency.
energy), ⇥ , for Carnot en
c second law and
0.6 beat the
e⇥ciency of a non-ergodic engine which acts as an effective o
mt
0.5
Example:
electric ηengines
combustion engines.
η3 vs.
of three-dimensional ideal gas Lenoir engine, 5/3 .
iency η
D
0.4
η
Reason for higher efficiency of non-­‐ergodic engines. Need to release less entropy to the environment (P. Mehta and A.P., 2012). Ideal gas engine (Lenoir cycle)
I)  Deposit energy at constant volume
II)  Push piston until pressure drops to
equilibrium
III)  Relax back to equilibrium at
constant pressure
If the energy is induced along the x-­‐axis and the work cycle is shorter than the tehrmaliza>on >me get a higher efficiency. Closely related research: informa>on theory (Szilard engine), Informa>onal thermodynamics (realizing Maxwell’s daemons), informa>on and reversibility. Gauge transforma>ons in quantum systems Canonical transforma>ons = equa>ons of mo>on. Gauge poten>al = momentum operator Hamiltonian equa>ons of mo>on in a moving frame Special instantaneous frame, where U diagonalizes instantaneous Hamiltonian. This frame is convenient to study the non-­‐adiaba>c response perturba>vely. General theory of non-­‐adiaba>c response (with L. D’Alessio, 2013) Go to the interac>on (adiaba>c Heisenberg) picture with respect to . Use standard perturba>on theory Calculate expecta>on values of observables Expand the rate near t’=t. Simple expression which contains a lot Off-­‐shell Berry curvature Mass tensor High-­‐temperature (classical limit). Reduces to the equipar>>on theorem On-­‐shell: F’ – asymmetric fric>on, Fric>on tensor Posi>ve temperature guarantees simultaneous posi>vity of η, κ (second law of thermodynamics) (Barankov, Levitov, Spivak; Yuzbashyan et. al.; Andreev, Gurarie, Radzihovsky; Chandran et. al., …) Need to solve coupled self-­‐consistent equa>ons of mo>on. Adiaba>c limit: Born-­‐Oppenheimer approxima>on. Berry (1989) – quantum correc>on to the Born-­‐Oppenheimer force, given by the Fubini-­‐Study metric. Our goal: go beyond adiaba>c approxima>on. The Hamiltonian H0 is just to build intui>on, e.g. Zero temperature + gap: recover macroscopic Hamiltonian (Newtonian) dynamics. Can always find a canonical momentum 1
1 ˙ equa>ons ˙ ⌫˙d(m
˙ µimplication.
~~)in tAt
~a)nd Hamiltonian These w=˙ithout issipa>on can b
e )r˙ewriWen he L~agrangian L
+
)
+
A
(
V
(
)
E
(
(20)
~
~
⌫µ
µ
µ
0
tion
(19)
has
another
interesting
zero
temperature
(m
+
)
+
A
(
)
V
(
E
(
)
(20)
⌫
⌫µ µ2
µ µ
0
form 2 At zero temperature 0
ion.
ipative tensors (⌘ and F ) vanish (unless the system is tuned to a
~ ) = h0
~ )|0 i
the
system
tuned
to
a low-dimensional
reproduces
Eq.
(19)
where
Aµ (i~ and
) = h0
|A
|0
ih0and
E~0)|0
([26]).
|H(
~
~
µexcitations
oint
or if itAis
has
gapless
In
this
19)
where
(
)
=
h0
|A
|0
E
(
)
=
|H(
i
µ
µ
0
excitations
[26]).
In
this
are Berry
the
of the as
Berry
connection equations
and
Hamiltonian
(5))
in the
(19)
can value
beconnection
viewed
a Lagrangian
fact,
it inthe
and
Hamiltonian
(see
(5))ofinmotion.
the(see
in- If
of motion.
If fact, it ground state and we have used (see Eq. (16)):
stantaneous
(~Lagrangian:
-dependent)
otions
see that
the
ependent)
ground
state and we have used (see Eq. (16)):
!
!
@Aµ @A
1⌫ ˙ = i [@⌫ h0 |@µ 0˙ i @˙ µ h0 |@!
!
0
i]
=
ih0
|
@
@
@
i = F⌫µ .
~⌫@) V@ (~@) |0E⌫i0 (=
~µ)F .µ @ ⌫ |0(20)
L
=
(m
+
)
+
A
(
@⌫(h0
|@
0
i
@
h0
|@
0
i]
=
ih0
|
@
⌫
⌫µ
µ
µ
µ
~
~
@ ) ⌫ µE@02(µ ) µ
⌫
µ
µ
⌫
⌫µ
⌫(20)
From the Lagrangian (20)
we can define the canonical
conjugate
~ )the
~ ) =momenta
~ )|0
es
Eq.
(19)
where
A
(
=
h0
|A
|0
i
and
E
(
h0
|H(
i
~
~
ngian
(20)
we
can
define
canonical
momenta
conjugate
µ
µ
0
ndto Ethe
) = h0 |H( )|0
i -­‐ responsible for the Casimir force 0 ( coordinates
:
⌫
es
alue⌫ :of(see
the(5))
Berry
connection
and Hamiltonian (see (5)) in the inonian
in the
in@L
ous used
(~ -dependent)
ground
and we
have
(see
ave
(see
Eq.
(16)):
˙ µ used
~ ) Eq. (16)): (21)
p⌫ ⌘ state
=
(m
+

)
+
A
(
@L
⌫µ
⌫µ
⌫
p⌫ ⌘
= (m⌫µ + ⌫µ
)˙ ⌫˙ µ + A⌫ (~ )
(21)
@
˙
@!
!
!
A⌫ !
⌫
@ and
@ µithe
i
=
F
.
[@@⌫emergent
h0
0
i
@
h0
|@
0
i]
=
ih0
|
@
@
@
⌫=
µ @|@
⌫ |0
⌫µ
⌫
µ
µ @ ⌫ |0 i = F⌫µ .
µ
µ
⌫
Hamiltonian:
tµHamiltonian:
1
1
˙
nical
momenta
conjugate
H
⌘
p
L
=
A⌫ )(mthe
+ )canonical
Aµmomenta
) + V (~ ) +conjugate
E0 (~ ). (22)
e Lagrangian
can
1
⌫ ⌫ (20) we (p
⌫1 define
⌫µ~(pµ
2 ⌫µ (pµ Aµ ) + V ( ) + E0 (~ ). (22)
L = (p⌫ A⌫ )(m + )
ordinates
2
⌫:
Clearly the Berry connection term plays the role of the vector potential. Thus
yAconnection
plays
the
role of of
the
vector
potential.
H
amiltonian dynamics w
ith mHamiltonian
inimal c~oupling tThus
o the gauge fields. @L (21)
(~Emergent )see that term
we
the
whole
formalism
the
dynamics
for arbitrary
⌫
˙
p⌫ass ⌘rof
=Hamiltonian
(m⌫µ +term: ⌫µ )dynamics
A⌫ (1989 ) arbitrary
(21)
µ. +
whole
formalism
the
for
Without m
enormaliza>on M
B
erry ˙
macroscopic degrees
@ ⌫ of freedom is actually emergent. Without mass renorrees of freedom is actually emergent. Without mass renor-
Example: par>cle in a box Massless membrane. What mass will we measure? Mass of two walls is not equal to the sum of masses of each wall measured separately!. Mass of photons coming. Mass renormaliza>on near a quantum cri>cal point Mass has a singularity near QCP. Scaling dimension of the mass density Mass diverges for Below cri>cal dimension it can be hard to pass through QCP From a snowball to infla>on in cosmology (hypothe>cal scenario) Scalar field rolls affec>ng the Higgs mass. Near QCP (zero Higgs mass) it gets very heavy and dynamically localizes. The Kibble-­‐Zurek type scaling argument Scaling dimension of velocity Divergent KZ correla>on length Characteris>c gap Energy (heat) density Ini>al kine>c energy Can expect localiza>on if Localiza>on from the Kibble-­‐Zurek Localiza>on is expected if we absorb more energy than it has The slower the system goes the more likely it is localized Same criterion for the localiza>on as from the mass divergence. Not really surprising from understanding the scaling theory. Check numerically. Transverse field Ising model First subtract the GS energy so that the field moves in a flat poten>al (later revise this assump>on). Trapping condi>on Expect trapping when Observe sharp transi>on to the trapping regime at 0.1
0.0
0.1
0.2
0.1
0.3
0.4
0.5
0
0.01
1
2
1
10
3
4
5
Finite slope Start from the rest at some and release the system. What will happen? Naïve answer: will roll down, perhaps stumble a bit near QCP and move on. Wrong! The system can be truly self-­‐trapped due to hea>ng Expect two scenarios: Untrapped (adiaba>c) Trapped (enough hea>ng) Start far from QCP: not too fast Start near QCP : not too slow Expect trapping when Trapping is possible only if Numerical phase diagram Numerical constants are not very small, but this is quite typical. Interes>ng non-­‐equilibrium dynamics if start near QCP. Bare mass is irrelevant and can be set to zero. 5
100
µ =1,
80
60
µ =10,
=0.0001
=0.0001
µ =1,
=0.0003
µ =1,
=0.0010
µ =1,
=0.0030
40
20
0
0.00
(c)
0.05
0.10
Sc a le d tim e
0.15
Except for transients and long >mes have a full scaling collapse 0.20
Outlook: dynamic trapping is consistent with thermodynamic trapping Consider a fixed energy state. Equilibrium: maximize entropy The entropy is maximized near QCP where excita>ons are cheapest. From scaling expect entropy maximum near QCP for finite range of slopes. Typical phase diagram of cuprates Image: D. M. Broun, Nature Phys. (2008) QCP is a natural place for localizing a macroscopic DOF like an order parameter. Similar to the order by disorder scenario. Summary •  ETH -­‐> thermodynamics •  Relaxa>on in weakly nonintegrable systems through prethermaliza>on •  Recover macroscopic Hamiltonian dynamics from >me scale separa>on •  Divergence of mass near cri>cal points. Dynamical self-­‐
trapping near quantum cri>cal points. F. Essler, talk at KITP, 2012 5. Generalized Gibbs Ensemble
a par>cular (transverse field Ising) mof
odel IProve local
(in space)
integrals
motion [Im, In]=[I
m befor Works both for equal and non-­‐equal >me correla>on func>ons. Need only integrals of mo>on, which “fit” to the subsystem our
case
In =
X
j
In (j, j + 1, . . . , j +
n)
If we can not measure In – have too many fisng parameters. What if integrability is slightly broken?