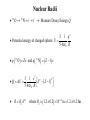Download Nuclear Structure, Nuclear Force

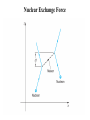
Nuclear Structure, Nuclear Force
Gocha Khelashvili, Ph.D.
Nuclear Structure
•
•
•
•
•
•
•
•
•
Composition of the Nucleus
Atomic Constituents
Nuclear Shape
Nuclear Stability
The Nuclear Force
Liquid – Drop Model
SEMF
Binding Energy
Nuclear Force Revisited
Nuclear Constituents
• Z - number of protons (charge of the nucleus).
• The nucleus has a mass ≈ A ⋅ m p - led to believe that nucleus
has A protons
1
• The nucleus has a chagre Z ≈ A
2
Is there Electron inside of Nucleus?
• Before discovery of neutron it was believed that there are A − Z
electrons inside of nucleus.
• The existance of electron inside of nucleus was supported by the
observation of β − radioactive decay, in which electrons are ejected
by certain radiocative nuclei.
• There were significant problems with this model.
Is there Electron inside of Nucleus?
• Uncertainity Principle → in order for electron to be confined in the
region of r < 10−14 m, electron should have Emin ≈ 100 MeV energy.
• Hovewer, energies of electrons in β decay are 1-2 MeV.
• There is no evidence of force  50-100 MeV between electron and
nuclei.
Is there Electron inside of Nucleus?
• If Ee < 0 - electron would never escape
• If Ee > 0 - There is no barrier to overcome;
All naturally occuring β emitters should
have dissapeared from the Earth long time
ago.
Is there Electron inside of Nucleus?
e
• µ N = - measured magnetic moment of nuclei (order or nuclear magneton).
2m p
e
• µB =
2me
- should be of order or Bohr magneton if electron is inside
of nuclei.
•
µN
1
- measurement shows 2000 times smaller magnetic momentum
≈
µ B 2000
compared to Bohr magneton.
Is there Electron inside of Nucleus?
•
14
N - nitrogen nucleus - angular mometum has quantum number 1 (observed in
hyperfine structure).
• If 14 N containes 14 protons and 7 electrons, the resulting angular momentum
would have quantum numbers 1/2, 3/2, 5/2 etc. It would be Fermion and it
would obey Fermi-Dirac statistics.
• But it obeys Bose-Einstein statistics.
• Rutherford suggested existance of neutral particle, possibly a bound state
of proton and electron and called it neutron
Discovery of Neutron
•
1930 W. Bothe and H. Becker - Alpha particles incident
on a beryllium foil cause the emission of uncharged
radiation capable of penetrating lead.
•
1932 Irene Joliot-Curie and Frederic Joliot - Protons of up
to 5.7 MeV are ejected when the radiation strikes a
paraffin slab. They assumed that radiation consisted of
gamma ray photons and the protons are knocked out of
the hydrogen-rich paraffin in Compton collisions.
•
Using Compton’s theory they estimated energy of
incident gamma rays and found that energies must be at
least 55 MeV.
•
1932 James Chadwick - Radiation consists of neutral
particles of approximately proton mass. In this case their
energies need not exceed 5.7 MeV since in head on
collision between particles of the same mass all energy is
transferred to target particles – protons.
Composition of the Nucleus
• After Chadwick's discovery of neutron
the idea of neutron being a tightly bound
state of proton and electron was abandoned
Composition of the Nucleus
• Z - number of protons (charge of the nucleus).
• N - number of neutrons.
• A = Z + N - Mass number of nucleus.
• A particular nuclear species is called a nuclide.
• Nuclides are denoted by the chemical symbol of element with presuperscript
giving value of A -
16
O,
15
O,....
• Sometimes Z is given as presubscript - 158 O (not necessary - chemical symbol  Z )
• Sometimes N is given as subscript - 158 O7 (not necessary - N= A − Z )
• Isotopes - same Z (protons) and different N (neutrons) -
O and
15
O
• Isotones - same N (neutrons) and different Z (protons) - 13 C and
14
N
• Isobars - same A (neutrons + protons) -
14
C and
14
N
16
Composition of the Nucleus
Composition of the Nucleus
mass unit → =
u 1.66054 ×10−27 kg → mass of 126C is exactly 12u
Energy equivalent of mass unit → 931.49 MeV
Nuclear Radii
Nuclear Radii
Nuclear Radii
•
15
O → 15 N + e − +ν → Measure Decay Energy Q
3 1 q2
• Potential energy of charged sphere: U =
5 4πε 0 R
• q ( 15 O ) =
Ze and q ( 15 N ) =
( Z − 1) e
3 1 e2  2
2
•Q=
∆U =
Z − ( Z − 1) 

5 4πε 0 R 
•
R =R0 A1/3
where R0 ≈ (1.2 ± 0.2 ) ×10−15 m =1.2 ± 0.2 fm
Ground-State Properties of Nuclei
• After 27 MeV energy of alpha particle
experimental curve deviates from Rutherford
formula.
• Energetic alpha particle penetrates nucleus
deep enough to interact directly with protons
and neutrons with attractive nuclear force.
• Thus scattering intensity falls.
Nuclear Radii
• SLAC experiment (1953) - nuclei bombarded
with electrons having 200-500 MeV energies.
• λ ( 500 MeV electron )  2.5 fm (de Broglie
formula)
• 2.5 fm < radius of heavy nuclei
• Study a structure of heavy nuclei
by analyzing electron diffraction
patteren.
0.61λ
• First minimum - sinθ =
R
Nuclear Radii
Example: Using the data for 420 MeV electron scattered from
of
16
16
O, estimate the radius
O nucleus.
0.61λ
, where θ 440
=
sin θ
R
de Broglie wavelenght of 420 MeV electron - λ =
p c = E − ( mc
2 2
2
h
p
) = ( 420 ) − ( 0.511) ≈ ( 420 MeV )
2 2
2
2
2
or
p = 420 MeV/c → λ =
R
0.61 ⋅ 2.95
=
2.59 fm
0
sin 44
1239.8 ( eV ⋅ nm )
hc
−6
=
=
2.95
×
10
( nm ) = 2.95 fm
6
420 MeV
420 ×10 ( eV )
Nuclear Size and Shape
R = R0 A1/3
where R0 ≈ (1.2 ± 0.2 ) ×10−15 m =1.2 ± 0.2 fm
Example: find the density of the 126C nucleus
R ≈ 1.2 × (12 ) fm =
2.7 fm
1/3
m
ρ =
=
4
π R3
3
(12u ) (1.66 ×10−27 kg / u )
3
4 
−15
m
π
2.7
10
×


3 
2.4 ×1017 kg/m3 → 4 billion tons per cubic inch!
ρ=
(
)
The Nuclear Force – Range Behavior
• Strongly attractive component which acts only over short range
• At very short distances (<0.5 fm) repulsive component
• Equilibrium - leads to the saturation of nuclear force.
• Evidence - approximately constant density of nuclear matter.
The Nuclear Force – Charge Dependence
• Nuclear force is charge symmetric: n-n and p-p forces are the same in a given
state
• Evidence: Stability of nucleus N ≈ Z (A ≤ 40). This would not be a case if n-n
p-p forces are different.
• Why do we see different potentials on the picture above?
Stability Curve
• For A ≤ 40 → N ≈ Z for stable nuclei
• For A > 40 → N > Z for stable nuclei
Nuclear Stability
• Ignore electrostatic repulsion between protons for light nuclei (A ≤ 40)
• Energy is smallest if A/2 are neutrons and A/2 are protons
• Energy is greatest if there only one type of particle (exclusion principle)
The Nuclear Force – Charge Dependence
• For heavy nuclei (A > 40), electrostatic repulsion between protons becomes important.
• Potential energy becomes Z 2 dependent.
• The energy inceased less by adding two neutrons than by adding one neutron and one
proton.
• N − Z increases for stable nuclei with inceasing Z .
Stable Isotopes (N vs. Z)
• There are about 270 stable nuclides and about 100 different elements.
• 2.7 stable isotopes per element
• There are larger than average number of stable isotopes with nuclei
with Z equal 2, 8, 20, 28, 50, 82 and 126 (last is theoretical for now)
• "Magic Numbers" - closed shell structure, very much as "magic atomic
numbers" - 2, 10, 18 and 36 corresponds to closed-electron shell
structure.
The Nuclear Force – Charge and Spin
Dependence
• Nuclear force is almost charge idependent ≈ same for n-p, n-n and p-p

0
→S =
↑ 1/ 2 ↓ 1/2 
p-p

0
→S =
↑ 1/ 2 ↓ 1/2 
p-n


Force is stronger for S 1 state.
=
↑ 1/ 2 ↓ 1/2  → S 0,1 =
↑ 1/ 2 ↑ 1/2 
n-n
Binding Energy
Mass of 11 H atom
1.007825u
+ Mass of neutron
+1.008665u
Expected mass of 21 H atom
Measured mass of the
2
1
2.016490u
H atom is only 2.014102u (less than expected value)
=
∆m 2.016490u − 2.014102u
= 0.002388u
The energy equivalent of missing mass is:
∆E
=
( 0.002388u
)( 931.49 MeV/u )
2.224 MeV
Missing mass (energy) corresponds to energy given off when 21 H nucleus is formed
or it is energy required to break apart a deuterium nucleus into separate neutron and
proton
Binding Energy
Binding Energy per Nucleon
Nuclear binding energies are strikingly high. The range for stable nuclei is from
2.2 MeV for 21 H (deuterium) to 1640 MeV for
209
83
Bi (an isotope of the metal bismuth).
Typical binging energy is - 8 ×1011 kJ/kg − 800 billion kJ/kg
Boiling Water - 2260 kJ/kg (heat of vaporization)
Burning gasoline - 4.7 ×104 kJ/kg (17 million times smaller)
Binding Energy per nucleon =
( )
=
B 21 H
Total Binding Energy
A
(
)
1640 MeV
2.2 MeV
B 209
Bi
= 7.8 MeV
= 1.1 MeV and for=
83
209
2
Binding Energy Curve
Binding Energy Calculations
Example:
(a) Find the energy needed to remove a neutron from the nucleus of the calcium isotope
42
20
Ca.
(b) Find the energy needed to remove a proton from this nucleus
(c) Why are these energies different?
M
(
41
20
Ca
)
(
)
40.962278
41.958622
u , M 42
u M ( n ) 1.008665
u , M ( p ) 1.007276u
=
=
=
20 Ca
(a) 40.962278u + 1.008665
u 41.970943u =
u 0.012321u
=
→ ∆M 41.970943u − 41.958622
=
11.48 MeV
B = ( 0.012321 u ) × 931.49 MeV/u =
(b) Removing a proton from
42
20
Ca leavs the potassium isotope
41
19
K (40.961827 u). A similar
calculation give binding energy of 10.27 MeV for the missing proton
(c) Difference is due electrostatic repulsion between protons
Binding Energy Calculations
M N - mass of the nucleus, M A - mass of the atom,
me - mass of the electron, m p - mass of the proton, mn - mass of the neutron,
Batom =
M N c 2 + Zme c 2 − M Ac 2 =
∆mc 2 ≈ 0 (compared to Bnuclear )
B=
Zm p c 2 + Nmn c 2 − M N c 2 = Zm p c 2 + Zme c 2 + Nmn c 2 − ( M N c 2 + Zme c 2 )
nuclear



ZM H c 2
Bnuclear = ZM H c 2 + Nmn c 2 − M Ac 2
M Ac2
Liquid – Drop Model
Semiempirical Mass Formula
B =a1 A − a2 A2/3 − a3 Z ( Z − 1) A−1/3 − a4 ( A − 2 Z ) A−1 ± a5 A−1/2
2
23.7
Liquid – Drop Model
4

Evolume  V = π R 3 
a1 A
→ Evolume =
3

1/3

R = R0 A

Reason why the binding energy per nucleon is approximately constant
Liquid – Drop Model
• Correction to first term


− a2 A2/3
Esurface  S = 4π R 2  → Esurface =

R = R0 A1/3

• Implies fewer interactions for surface nucleus and thus smaller binding energy
• Explains sharp decline in the binding energy per nucleon at low A values.
Liquid – Drop Model
• Correction to first term


2
3 ( Ze )

− a3 Z 2 A−1/3
 Z 2 A−1/3  → Ecoulomb =
Ecoulomb =
5 4πε 0 R

1/3

R = R0 A

• Energy of repulsion decreases the binding energy (thus < 0)
• Explains slow decline in the binding energy per nucleon at large A values.
Semiempirical Mass Formula
SEMF – Asymmetry Energy
N − Z = A − Z − Z = A − 2Z
ε
energy incease   1
 1
=
−
−
N
Z
N
Z
(
)
(
)
 
  2
new
neutron
2 

 2
ε
ε
2
2
∆E
=
−
=
−
2
N
Z
A
Z
(
)
(
) →E
2
=
∆
=
−
−
2
E
a
A
Z
A−1
(
)
8
8
assymetry
4

−1
εA

∆
=
E
( number of new neutrons ) 
SEMF – Pairing Energy
E pairing = ± a5 A−1/2
• The last term arises from the tendency of proton pairs and neutron pairs to occur.
• Even-even nuclei are most stable and have higher binding energies than would
otherwise expected
• Such nuclei as 42 He,
12
6
C and
16
8
O appear as peaks on the empirical curve
• Odd-Odd nuclei have both unpaired protons and neutrons and have relatively low B.E.
Weizsäcker’s SEMF
23.7
23.7
More Binding Energy Calculations
Example:
The atomic mass of the zinc isotope
64
30
Zn is 63.929 u. Compare its binding energy with the
prediction of SEMF
Solution:
The binding energy of
64
30
Zn is:
Eb = ( 30 )(1.007825 u ) + ( 34 )(1.008665 u ) − 63.929 u  × ( 931.49 MeV/u ) =
559.1 MeV
Using SEMF:
( 0.75 MeV )( 30 )
Eb = (15.67 MeV )( 64 ) − (17.23 MeV )( 64 ) −
1/3
( 64 )
2/3
+
12 MeV
( 64 )
1/2
554.1 MeV
=
Eb 559.1
Eb 554.1
=
= 8.73 MeV or=
= 8.66 MeV
A
64
A
64
less than 0.1% difference
2
−
( 23.7 MeV )(16 )
64
More Binding Energy Calculations
Nuclear Exchange Force
Nuclear Exchange Force
Electrostatic Interaction (Classical Picture)

Distribution of charge produces an electric field E , and the force felt by another charge q


located in the field is the product qE. Any change in the charge distribution changes E ,
however, the information that change has occured does not appear instantaneously throughout
the field, but it is propageted outward at the speed of light
Electrostatic Interaction (Quantum Mechanical Picture)
Every charge is continually emitting and absorbing photons, even when it is not moving. These
photons are called virtual photons, meaning they are not directly observable. A charge can emmit
a virtual photon of energy hf without changing its energy or recoiling. Energy and momentum
conservation laws are not violated provided that photon exists for no longer than ∆t=  / ∆E ,
hf , as required by uncertainty principle.
where ∆E =
R = c∆t =
λ
c c
c
=
=
=
∆E hf 2π f 2π
Nuclear Exchange Force
1935 Hideki Yukawa
Nuclear interaction is carried out by
virtual particles - mesons
Short Range - meson has a mass
∆E ≥ mc 2

c
 1 fm
=
∆E mc
m ≈ 3.5 ×10−28 kg ≈ 380me ≈ 200 MeV/c 2
R = c∆t =
Charge Independence - mesons carry + e, 0, - e charge
Experimentaly π ± , π 0 are found in 1947
mπ ≈ 140 MeV/c 2
Nuclear Exchange Force
Probability Density of the Exchange Mesons
Virtual Meson Exists :
(
)
1.055 ×10−34 J×s

−24
s
∆t =
=
=
5
×
10
2
2
2
−13
mc
140 MeV/c c 1.6 ×10 J/MeV
(
)( )(
)
Thus, a 10−20 second time-exposure "snapshot" of a nucleon would show a cloud
consisting more than 10,000 mesons surrounding the nucleon!
(
)


2
2
∂
Φ
r
,
t
(
)

1
mc




2
⇒
∇
Φ
r
,
t
−
=
Φ
r
,t)
(
)
(



2
2
∂
c
∂t
  
E → i , p 2 → −  2∇ 2 
∂t

mc 2 = E 2 − ( pc )
2
2
Probability Density of the Exchange Mesons

2
2
∂
Φ
r
,
t
(
)
1
mc




∇ 2Φ ( r , t ) − 2
=
Φ
r

 ( , t ) → For stationary solution →
2
c
∂t
  
Ae − r / R
  mc 


2
∇ Φ ( r=
)   Φ ( r ) → Φ ( r=)
r
  
2
−2 r / R
 2 A e
Probability Density → Φ ( r ) = 2
r
2
→
Probability Density of the Exchange Mesons
• For r > 0.5 R curve agrees with experimental
results.
• Breaks down for r < 0.5 R
• Measured meson density is much lower than
figure would suggest
• Reason - at r < 0.5 R quark composition
of nuclei and mesons becomes important
• Decrease in meson density is due to saturation of strong force - called assymtotic
freedom of quarks.
QCD – Asymptotic Freedom
• For low r , strong force is
diluted by gluon selfinteractions.
• α S → 0 faster than
1
r
• For r < 10−18 m, quarks move
as almost free particles.
• Asymtotic Freedom confirmed by electron
deep scattering experimensts.
QCD – Asymptotic Freedom
Quark Confinement
VQCD ( r ) = −
4α S
4α S
+ kr , FQCD ( r ) = −∇VQCD ( r ) =
−k
2
3r
3r
lim VQCD ( r ) → ∞,
r →∞
lim FQCD ( r ) → const
r →∞