Download r - TTU Physics

Central Field Orbits Section 8.5
• We had, (for a GENERAL central potential!):
Radial velocity r vs. relative coordinate r
r(r) = (2μ)-1([E - U(r)] - [2(2μr2)])½
Time vs. r
t(r) =  (2μ-1)∫dr([E - U(r)] - [2(2μr2)])-½
Derivative of θ with respect to r
(dθ/dr) =  (r-2)(2μ)-½[E - U(r) -{2(2μr2)}]-½
The Orbit θ(r)
θ(r) = ∫(/r2)(2μ)-½[E - U(r) - {2(2μr2)}]-½dr
• All of these quantities have the common factor:
([E - U(r)] - [2(2μr2)])½
(1)
• (1) should remind you of 1d where we analyzed the particle
motion for various E using an analogous expression & found
turning points, oscillations, phase diagrams, etc.
– It is similar to conservation of energy in 1d, which gives:
(dx/dt) = x(x) =  [(2m-1)(E - U(x))]½
• We now qualitatively analyze the RADIAL motion for a
“particle” of mass μ in the presence of a central potential U(r)
by methods similar to those used in Sect. 2.6 for 1d motion.
• Remember: The ACTUAL motion is 2 d!  We need to
superimpose angular the motion (θ) on the results for the
radial motion, to get the ORBIT θ(r) or r(θ).
• Look at the radial velocity vs. r:
r(r) = (2μ)-1([E - U(r)] - [2(2μr2)])½ (a)
We could use this to construct the r vs. r phase diagram! See
Goldstein’s graduate mechanics text.
• Or, conservation of energy:
E = (½)μr2 + [2(2μr2)] + U(r) = const (b)
• Define: Radial turning points  Points where r = 0
(the particle stops moving in the r direction!)
– Look at either (a) or (b) & find, at the radial turning points:
[E - U(r)] - [2(2μr2)] = 0
(1)
Turning Points
[E - U(r)] - [2(2μr2)] = 0 (1)
r(r) = (2μ)-1([E - U(r)] - [2(2μr2)])½ (2)
• The solutions r to (1) are those r where (2) = 0
Radial Turning Points are called Apsidal Distances
• Generally, (1) has 2 roots (the max & min r of the orbit)
 rmax & rmin  We know that rmax ≥ r ≥ rmin
The radial motion will be oscillatory between rmax & rmin.
• For some combinations of E, U(r), , (1) has only one root:



In this case, from (2) r = 0, for all t
r = constant
The orbit r(θ) will be CIRCULAR.
Closed & Open Orbits
[E - U(r)] - [2(2μr2)] = 0 (1)
r(r) = (2μ)-1([E - U(r)] - [2(2μr2)])½ (2)
• If the motion for a given U(r) is periodic in r, then
 The orbit r(θ) will be closed.  That is, after a
finite number of oscillations of r between rmax & rmin,
the motion will repeat itself exactly!
If the orbit does not exactly close
on itself after a finite number of
radial oscillations between
rmax & rmin, the orbit r(θ) will
be open. See figure 
• Use the orbit eqtn θ(r) to find the change in θ due to one
complete oscillation of r from rmin to rmax & back to rmin:
– Angular change = 2  the change in going once rmin to rmax:
 Δθ  2∫(/r2)(2μ)-½[E - U(r) - {2(2μr2)}]-½dr
(limits rmin  r  rmax)
Δθ |
|
Δθ = 2∫(/r2)(2μ)-½[E - U(r) - {2(2μr2)}]-½dr (rmin  r  rmax)
• Periodic motion & a closed orbit results if & only if the
angular change is a rational fraction of 2π. That is:
Δθ  2π(a/b) (a, b integers)  periodic, closed orbit.
• If the orbit is closed, after b periods, the radius vector the of
particle will have made a complete revolutions & the particle
will be at its original position.
• It can be shown (Prob. 8.35) that if the potential is a power
law in r: U(r) = k rn+1 a closed NON-CIRCULAR path can
occur ONLY for n = -2 (the inverse square law force: gravity,
electrostatics; discussed in detail next!) & n = +1 (the 3d
isotropic, simple harmonic oscillator of Ch. 3).
– Footnote: Some fractional values of n also lead to closed
orbits. These aren’t interesting from the PHYSICS viewpoint.
Centrifugal Energy & Effective Potential
Section 8.6
• Consider again the common factor in r, Δθ, θ(r), t(r), etc.:
([E - U(r)] - [2(2μr2)])½
• Qualitatively analyze the RADIAL motion for a
“particle” of mass μ in a central potential U(r) by
methods similar to those used in Sect. 2.6 for 1d
motion.
– Remember that the ACTUAL motion is in 2d!
 Must superimpose the angular motion (θ) on the
radial motion results, to get the ORBIT θ(r) or r(θ).
• Consider: ([E - U(r)] - [2(2μr2)])½
• Recall the physics of the term [2(2μr2)]! From previous
discussion (conservation of angular momentum;  = μr2θ):

[2(2μr2)]  (½)μr2θ2
 The angular part of the kinetic energy of mass μ.
• When it is written in the form [2(2μr2)], this
contribution to the energy depends only on r.
Because of this, when analyzing the r part of the
motion, we can treat this as an additional term in
the potential energy.  It is often convenient to call
it another potential energy term
 THE “CENTRIFUGAL” POTENTIAL ENERGY
Centrifugal Potential
[2(2μr2)] “Centrifugal” Potential Energy  Uc(r)
– As just discussed, this is really the angular
part of the Kinetic Energy!
 Consider the “Force” associated with Uc(r):
Fc(r)  - (∂Uc/∂r) = [2(μr3)]
Or, using  = μr2θ :
Fc(r) = [2(μr3)] = μrθ2  “Centrifugal Force”
Centrifugal Force
Fc(r) = [2(μr3)]  “Centrifugal Force”
• Fc(r) = A fictitious “force” arising due to fact that the
reference frame of the relative coordinate r (of the “particle”
of “mass” μ) is not an inertial frame!
– Its not a force in the Newtonian sense! (It doesn’t come from any
interaction of the “mass” μ with its environment!) It’s a part of the “μa”
(right!) of Newton’s 2nd Law, rewritten to appear on the “F” (left) side.
For more discussion, see Ch. 10.
• “Centrifugal Force” is an unfortunate terminology! Its
confusing to elementary (& also sometimes to advanced!) physics
students. Direction of Fc: Outward from the force center!
– I always tell students that there is no such thing as centrifugal force!
• For a particle moving in a circular arc, the actual, physical force in an
Inertial Frame is directed INWARD TOWARDS THE FORCE
CENTER  Centripetal Force [F = μrθ2 = μrω2 = μ(v2/r)]
Effective Potential
• Consider again: [E - U(r) - {2(2μr2)}]½
• For both qualitative & quantitative analysis of the
RADIAL motion for the “particle” of mass μ in the
central potential U(r), Uc(r) = [2(2μr2)] acts as an
additional potential & we can treat it as such!
– Recall that physically, it comes from the Kinetic Energy of
the particle!
 Its convenient to lump U(r) & Uc(r) together into
an Effective Potential  V(r)  U(r) + Uc(r)
V(r)  U(r) + [2(2μr2)]
• Effective Potential  V(r)  U(r) + [2(2μr2)]
• Consider now: r  [E - V(r)]½
(1)
• Given U(r), we can use (1) to qualitatively (&
quantitatively) analyze the RADIAL motion
for the “particle”. Get (radial) turning points,
(radial) oscillations, etc.
– Very similar to 1d where we analyzed
particle motion for various E using an
analogous expression.
• Consider now, an important special case (in the
mathematical sense) which is the MOST important
case in the physics sense!
• Consider the Inverse Square Law central force:
F(r) = - kr-2
 U(r) = - kr-1 = - (k/r)
– For convenience, take U(r)  0
Gravitational Force: k = GmM
Coulomb Force: (SI Units): k = (q1q2)/(4
• The Effective Potential for this case is:
V(r)  -(k/r) + [2(2μr2)]
0)
• Effective Potential, Inverse Square Law
force. (see figure): V(r) = -(k/r) + [2(2μr2)]
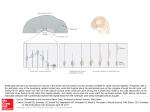
• Lets now qualitatively analyze the radial motion using V(r) for
the Inverse Square Law force (figure).
E = (½)μr2 + V(r)  E - V(r) = (½)μr2
 r = 0 at turning points (where E = V(r))
• Consider E ≥ 0
(E1 in figure): This
case corresponds to
E = E1
unbounded radial


motion. μ moves in
 r = r1
(½)μr2
from r =  towards

the force center (at

r = 0), “hits” the
barrier at (turning
point) r1 ( r = 0), and is “reflected” back to r = .
• Qualitative analysis of the radial motion using V(r) for the
Inverse Square Law force (figure).
E = (½)μr2 + V(r)  E - V(r) = (½)μr2
 r = 0 at turning points (where E = V(r))
• Consider
Vmin < E < 0 (E2 in
figure): This case
corresponds to
oscillatory radial
r = r2 E = E2 r = r4
motion. μ moves



back & forth between

 (½)μr2
(turning points) r2 &
Vmin
r4 ( r = 0). These turning points are the Apsidal Distances of
the orbit (the rmax & rmin from before).
• Qualitative analysis of the radial motion using V(r) for the
Inverse Square Law force (figure).
E = (½)μr2 + V(r)  E - V(r) = (½)μr2
 r = 0 at turning points (where E = V(r))
• Consider E = Vmin
= -(μk2)/(22) (E3 in
the figure): This case
corresponds to no
radial motion at all
r = r3
because r = 0 for all
E = E3


time. That is, the orbit

radius is constant
Vmin 
(r = r3 in the figure). That is, μ moves in a Circular Orbit!
• Note: E < Vmin is Not Allowed! (r would be imaginary!)