* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Chapter 22: Gauss`s Law
Magnetic monopole wikipedia , lookup
Geomorphology wikipedia , lookup
Weightlessness wikipedia , lookup
Aristotelian physics wikipedia , lookup
Aharonov–Bohm effect wikipedia , lookup
Field (physics) wikipedia , lookup
Lorentz force wikipedia , lookup
Maxwell's equations wikipedia , lookup
Nanofluidic circuitry wikipedia , lookup
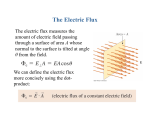
Chapter 22 1 Flux Number of objects passing through a surface 2 Electric Flux, F is proportional to the number of electric field lines passing through a surface Assumes that the surface is perpendicular to the lines If not, then we use a cosine of the angle between them to get the components that are parallel Mathematically: F E A cos E A 3 Simple Cases A A A F=EA F=0 E E F=EAcos E cos E 4 From S to A S represents a sum over a large a collection of objects Integration is also a sum over a collection of infinitesimally small objects, in our case, small areas, dA So F E dA Since dA represents dxdy then, technically, F E dA 5 Gauss’s Law The field lines emitted by a charge are proportional to the size of the charge. Therefore, the electric field must be proportional to the size of the charge In order to count the field lines, we must enclose the charges in some geometrical surface (one that we choose) 6 Mathematically Fq F Charge enclosed within bounding limits of this closed surface integral q 0 qenclosed E d A 0 7 Fluxes, Fluxes, Fluxes 8 3 Shapes Sphere Cylinder Pillbox 9 Sphere When to use: around spherical objects (duh!) and point charges Hey! What if an object is not one of these objects? Closed surface integral yields: 2 E d A E ( 4 r ) r is the radius of the geometrical object that you are creating 10 Sphere Example What if you had a sphere of radius, b, which contained a material whose charge density depend on the radius, for example, =Ar2 where A is a constant with appropriate units? Inside the sphere : qenclosed V 4 3 4 ( Ar )( r ) Ar 5 3 3 2 qenclosed 2 E d A E ( 4 r ) 4 E (4r ) Ar 5 3 0 Outside the sphere : qtotal V 4 3 4 ( Ab )( b ) Ab 5 3 3 2 qenclosed 2 E dA E (4r ) E (4r 2 ) 2 E A 3 r 3 0 4 Ab 5 3 0 A 5 b 3 0 E r2 At r=b, both of these expressions should be equal 11 Cylinder When to use: around cylindrical objects and line charges Closed surface integral yields: E dA E (2rL) L r is the radius of the geometrical object that you are creating and L is the length of the cylinder 12 Cylinder Example E dA E (2rL) What if you had an infinitely long line of q enclosed lL charge with a linear lL charge density, l? E (2rL ) 0 l l E or E rˆ 2r 0 2r 0 13 Pillbox When to use: around flat surfaces and sheets of charge Closed surface integral yields: E dA EA A is the area of the pillbox 14 Charge Isolated Conductor in Electrostatic Equilibrium If excess charge is placed on an isolated conductor, the charge resides on the surface. Why? If there is an E-field inside the conductor then it would exert forces on the free electrons which would then be in motion. This is NOT electrostatic. Therefore, if there is no E-field inside, then, by Gauss’s Law, the charge enclosed inside must be zero If the charges are not on the outside, you are only left with the surface A caveat to this is that E-field lines must be perpendicular to the surface else free charges would move. 15 Electric field on an infinitely large sheet of charge Let q A A E +++++++++++++++++++++++++++++++++++++++++++++ E E dA EA ( E )( A) 2 EA qenclosed A So 2 EA A 0 E 2 0 or E nˆ 2 0 16 Electric field on a conducting sheet Let q A A E +++++++++++++++++++++++++++++++++++++++++++++ E dA EA 0 EA qenclosed A So So a conductor has 2x the electric field strength as the infinite sheet of charge A 0 E or E nˆ 0 0 EA 17 A differential view of Gauss’s Law Recall the Divergence of a field of vectors Div (v ) v How much the vector diverges around a given point Div=+large Div=0 18 Divergence Theorem (aka Gauss’s Thm or Green’s Thm) v d v d A Suspiciously like LHS of Gauss’s Law A place of high divergence is like a faucet Bounded surface of some region Sum of the faucets in a volume = Sum of the water going thru the surface 19 Div(E) qenclosed E dA 0 qenclosed E d 0 and qenclosed d so E 0 So how the E-field spreads out from a point depends on the amount of charge density at that point 20