* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Chapter 1 Chemical Foundations
Big O notation wikipedia , lookup
Mathematics of radio engineering wikipedia , lookup
History of mathematical notation wikipedia , lookup
History of logarithms wikipedia , lookup
Large numbers wikipedia , lookup
Location arithmetic wikipedia , lookup
Elementary arithmetic wikipedia , lookup
Approximations of π wikipedia , lookup
Elementary mathematics wikipedia , lookup
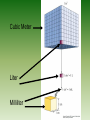
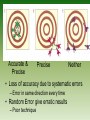
Chapter 1 Chemical Foundations AP Chemistry Objectives • • • • Recall units of measure Describe uncertainty in measurement Use scientific notation for numbers Apply significant figure rules Units of Measure • SI Base Units – Mass • Kilogram – kg • 1 kilogram is about 2.20 pounds – Length • Meter – m • 1 meter is about 3 feet Units of Measure • Time – Second – s – The time needed for a cesium-133 atom to perform 9,192,631,770 complete oscillations. • Temperature – Kelvin – K – 273 K = 0 degrees C • Amount – Mole – mol – 1 mol = 6.022x1023 particles Units of Measure • Current – Ampre – A • Luminous Capacity – Candela – cd • First five are the most commonly used in chemistry Volume • Volume is not an SI Base Unit – Metric system – Powers of 10 • 1 Liter is 1/1000 of a cubic meter • 1 Liter (L) = 1000 cm3 = 1000 mL Cubic Meter Liter Milliliter Volume? • Uncertainty is in the last digit. Accuracy and Precision • Accuracy – The nearness of a measurement to its accepted value • Precision – The agreement between numerical values – You can be precise without being accurate Accurate & Precise Precise Neither • Loss of accuracy due to systematic errors – Error in same direction every time • Random Error give erratic results – Poor technique Significant Figures • All known digits plus one estimated digit in a measurement What is the length? • 2 Sig. Fig • 1 Known Digit • 1 Estimated Digit Significant Figures • Rule #1 – All Nonzero digits are significant – Ex. 76.44 mL – Ex. 285.85 s Significant Figures • Rule #2 • “Captive Zeros” • Zeros appearing between nonzero digits are significant • Ex. 308.2001 g = Significant Figures • Rule #3 • “Leading Zeros” • Zeros appearing in front of nonzero digits are not significant • Ex. 0.007036 g • Takes care of unit changes Significant Figures • Rule #4 • “Ending Zeros” • Ending zeros are significant if there is a decimal place • Ex. 53.00 m • Ex. 40000. m • Ex. 40000 m • 40000. is much more precise than 40000 What is the length? Significant Figures • Rule #5 • “Exact Numbers” • Exact number have an unlimited number of significant figures • Exact numbers are counting numbers or definitions • 2 cars or 1000g/1kg Significant Figures • Rule #6 • “Scientific Notation” • All numbers that come before the x10n are significant – Must be in proper form • Ex. 3.33x105 • Ex. 2.04x10-4 Rounding • • • • • • • 5 and larger round up 4 and smaller round down Round the following 34.567 to 2 SF = 756.44 to 4 SF = 0.004325 to 3 SF = 3436543 to 2 SF = Addition and Subtraction w/ SF • Addition and Subtraction – The answer must have the same number of digits to the right of the decimal as there are in the measurement having the fewest digits to the right of the decimal point – Ex. 12.11 m + 15 m = – Number of SF’s does not matter! Multiplication and Division w/ SF • Multiplication and Division – The answer can have no more SF’s than are in the measurement with the fewest total SF’s – Ex. 55 m / 11.34 s = Scientific Notation • A method of representing very large or very small numbers • M x 10n – M is a number 1 or larger and less than 10 – n is an integer (positive or negative) – All digits in M are significant (If in proper form) Converting to Sci. Notation • Move decimal so that M is between 1 and 10 • Determine n by counting the number of places the decimal point was moved – Moved to the left, n is positive – Moved to the right, n is negative Examples • 340,000,000 = • 5.04x105 = • 0.00000300 = • 2.212x10-4 = Sci. Notation on Calculators • Enter digits in you calculator using the EE key. • For TI 83’s it is the 2nd of the comma • For TI 30’s it is a key • Saves key strokes • Fewer OOR mistakes • 3.4x106 = 3.4E6 • 7.4x10-5 = 7.4E-5 Sci. Notatation Math Operations • Multiply and Divide – Multiply or divide first number – Add exponents (Multiply) – Subtract exponents (Divide) • Addition and Subtraction – Exponents must be the same – Then add or subtract first number – Exponents stay the same Calculations • • • • 3.0x105 + 4.0x105 = 4.0x103 – 2.0x102 = 7.0x105 * 2.0x104 = 8.0x106 / 4.0x10-3 = • _____4.5x104____ = 6.2x106 * 3.1x10-8 Objectives • • • • • Recall metric prefixes Convert numbers from one unit to another Describe different temperature scales Explain density and perform calculations Classify matter into groups The Metric System • A system based on powers of ten • Uses SI Units • Allows easy work with both large and small numbers • Prefixes tell us which power of 10 we are using SI Prefixes (10x larger) Page 9 in your book • • • • • • • Tera Giga Mega Kilo Hecto Deca Base T G M k h da 1012 109 106 103 102 101 100 1000000000000 1000000000 1000000 1000 100 10 1 SI Prefixes (10x smaller) • • • • • • • • Base Deci Centi Milli Micro Nano Pico d c m μ n p 100 10-1 10-2 10-3 10-6 10-9 10-12 1 .1 .01 .001 .000001 .000000001 .000000000001 Conversions • To convert between units set up conversion factors – Ratios of equality 3 1000mm 1x10 m 1m 1km Convert 67 kg to g Convert 450 cL to dL Convert 8 3.4x10 ng to kg Converting From Metric To English • Find ratios that are true – Page 18 has some equivalents 39.4in 2.54cm 1in 1m Convert 763 cm to yd Convert 1.2 mi/hr to ft/s Convert 2 2 3.8 m /hr to cm /s Temperature • • • • • Many different temp. scales All 0 marks based on different ideas 0 ºF Coldest saltwater stays a liquid 0 ºC Normal Freezing Point of water 0 K Molecular motion stops 1 K = 1 ºC = 1.8 ºF Temperature Conversion • Temp K = 273 + Temp C • Temp C = Temp K – 273 • 0 ºC = 273 K • If you need any others look up the equ. • TC= (TF – 32)(5/9) • TF = TC(9/5) + 32 Density • Ratio of mass to volume • Density = __Mass__ Volume • Periodic Trend • Units – Solids – g/cm3 – Liquids – g/mL – Gases – g/L Density Determination • Mass is determined on a balance • Volume is measured in two ways – Regular objects can be measured – All objects can use water displacement Density • Physical Property – Can be used to identify a substance Lead 11.35 Iron 7.87 Magnesium 1.74 Zinc 7.13 Copper 8.96 Example: A metal cube has sides measuring 3.00 cm. It has a mass of 242.13g. What is the density? What is the metal? Density • Physical Property – Can be used to identify a substance Lead 11.35 Iron 7.87 Magnesium 1.74 Zinc 7.13 Copper 8.96 Homework • p.33 #'s 33a-f,36a-d,42 47,57,68