Download Quantum Dimer Models on the Square Lattice

Quantum Dimer Models on the Square Lattice
In collaboration with D. Banerjee, M. Bogli, C. Hofmann, P. Wilder, and U.-J. Wiese (PRB 90,
245143 (2014) and arXiv:1511.00881). Some of the figures and content are from Debasish,
Philippe, Pascal, and online sources, in particular the preprint arXiv:0809.3051.
F.-J. Jiang
Physics Department, Nataional Taiwan Normal University, Taipei, Taiwan
Nov. 2015
Outlines
◮
Introduction: why quantum dimer models.
◮
The established (conjecture) ground state phase diagrams of
QDM.
◮
Connecting QDM on the square lattice with U(1) Quantum link
model (QLM).
◮
Results : the phase diagram of QDM on the square lattice.
◮
Conclusions.
Introduction
◮
In 1986, high temperature (Tc ) superconductivity was discovered
in doped cuprate materials.
◮
Since then a lot of efforts have been devoted to understanding
the mechanism behind high Tc superconductivity.
It is believed that high temperature cuprate superconductors are
obtained by doping antiferromagnets with holes or electrons.
◮
◮
Notice although it is established experimentally that
antiferromagnets have massless excitations, no long-range order
is found in high temperature cuprate superconductors.
◮
This experimental observation plays the crucial role in
constructing the Quantum dimer models (on the square lattice).
Heisenberg and Hubbard models
◮
The relevant model for an antiferromagnet (on the square lattice)
is the spin-1/2 Heisenberg model:
X
H=J
S~x · S~y .
hxyi
◮
The relevant model for cuprate high temperature superconductor
(or doped antiferromagnets) is the Hubbard model:
X +
ci,σ
cj,σ + H.c.
H = −t
hi,ji,σ
+U
X
i
ni↑ ni↓ − µ
X
i
(ni↑ + ni↓ )
Heisenberg and Hubbard Models
◮
◮
At half filling (µ = U/2) and U → ∞, the Heisenberg model is
recovered from Hubbard model (identifying 4t 2 /U with J and
~ = c † ~σ c).
S
2
Quantum Dimer Models (QDMs)
◮
◮
Cuprate turns into a high temperature superconductor when
doping density x exceeds a critical value (x ≤ 0.2) → most of
lattice sites are still occupied by a SU(2) spin.
Since no long-range order is observed in high temperature
cuprate superconductors, one natural candidate degree of
freedom for these high Tc materials is the SU(2)-singlet.
◮
Resonating valence bond theory: first introduced by
P. W. Anderson in 1987 in order to understand high temperature
(cuprate) superconductor.
◮
Electrons from neightboring copper atoms interact to form a
valence bond (singlet, RVB). In particular, the valence bond lucks
the electrons inside it.
◮
These electrons can act as mobile Cooper pairs and can
superconduct when the cuprate is doped.
Quantum Dimer Models (QDMs)
◮
Quantum dimer models (QDMs) were introduce by Rokhsar and
Kivelson to model the physics of RVB in lattice spin models.
◮
In addition to (might) be relevant to high temperature cuprate
superconductors, QDMs are interests from the point of view of
condensed matter physics as well.
◮
Quantum deconfined criticality.
◮
Spin liquid.
◮
Topological order.
◮
Fractionalized spinors.
◮
These are the reasons why QDMs are interesting and have
attracted a lot of investigation during the last two decades.
Quantum Dimer Models (QDMs)
◮
Degree of freedom: SU(2) singlet valence bonds (or dimers):
=
√1 [|
2
↑↓i − | ↓↑i]
=
◮
Hamiltonian:
X
H =
[−J (|k ih= | + | =ihk |) + λ (| =ih= | + |kihk|)]
=
◮
HJ + Hλ .
Constraint: Every site touches exactly one dimer, no long-range
dimers and no polymers.
Quantum Dimer Models (QDMs)
◮
One example of configuration in quantum dimer model on the
square lattice:
Quantum Dimer Models (QDMs)
H
=
X
=
HJ + Hλ .
[−J (|k ih= | + | =ihk |) + λ (| =ih= | + |kihk|)]
HJ
HJ
Hλ
◮
◮
Hλ
The kinetic term flips plaquettes (namely, turns a horizontal pair of
dimers into a vertical one and vice-versa) and the potential term counts
flippable plaquettes.
The phase diagrams of QDMs
◮
Intuitively, the system will try to maximize the number of flippable
plaquettes when λ/J → −∞.
◮
On the square lattice, such state can be obtained by arranging
the dimers in a columnar pattern (four-fold degenerate):
The phase diagrams of QDMs
◮
On the contrary, the system will try to minimize the number of
flippable plaquettes when λ/J → +∞.
◮
On the square lattice, such state can be obtained by arranging
the dimers in a staggered pattern (many such states:
superposition of close-pack arrangement of dimers):
The phase diagrams of QDMs
◮
Plaquette arrangement of dimers (in the mean field sense,
four-fold degenerate, only found on 2D bipartite lattices):
The phase diagrams of QDMs
◮
Mixed states:
|statesi = c1 |ki + c2 | =i.
The phase diagrams of QDMs
columnar
???
plaquette
staggered
λ
RK
◮
2d bipartite lattices. The ??? is a first order transition for
honeycomb lattice.
The phase diagrams of QDMs
columnar
???
Z2 RVB liquid
staggered
λ
RK
◮
2d (and higher d) non-bipartite
The ??? is a unknown
√
√ lattices.
phase (could be so-called 12 × 12 phase) for triangular
lattice.
◮
Z2 RVB phase: a phase with Z2 topological order, i.e. there are
four-fold degenerate gapped ground states for 2d lattice with
periodic boundary condition. In particular, it has nontrivial
excitations. It is a liquid phase because all dimer correlations
decay exponentially.
The phase diagrams of QDMs
columnar
???
U(1) RVB liquid
staggered
Coulomb
λ
RK
◮
higher d bipartite lattices. The ??? is unknown for cubic lattice.
◮
U(1) RVB phase: gapless with algebraic dimer correlations. It is
called Coulomb phase as well because it has a continuous
description that resembles the usual Maxwell action of the free
electromagnetic field.
U(1) QLM
◮
Motivated by the (lattice QCD) Wilson action (Brower,
Chandrasekharan and Wiese, 1997, 1999).
◮
The same symmetry properties.
◮
The same algerbra relations.
◮
Finite-dimensional Hilbert space.
U(1) QLM
◮
The Hamiltonian of U(1) QLM:
i
Xh
†
† 2
J(U + U
) − λ(U + U
) = H1 + H2 .
H=−
◮
◮
†
†
U = Uwx Ux,y Uzy
Uwz
is the typical plaquette operator formed by
+
+
quantum links Uxy = Sxy
, where Sxy
is a raising operator of
3
electric flux Exy = Sxy which is built from a quantum spin-1/2 of
the link xy.
Notice the charges Qx at each site x can be determined from it
neighboring electric flux by
Qx = Ex,x+1̂ + Ex,x+2̂ − Ex−1̂,x − Ex−2̂,x .
◮
For QLM, the Gauss law restrictsP
the system to gauge invariant
states → Gx |ψi = 0. Here Gx = i (Ex,x+î − Ex−î,x ) is the
infinitesimal U(1) gauge transformations and Gx commutes with
the Hamiltonian.
U(1) QLM
◮
Represent the two possible states of electric flux for a link by the
LHS figure. Then in the flux space, a typical configuration of U(1)
QLM is given by the RHS figure.
+ 21 flux
− 21 flux
Symmetries of U(1) QLM
◮
Symmetris of QLM:
◮
U(1) symmetry.
◮
CTi .
◮
90 degrees rotation.
◮
CO ′ .
◮
U(1)2 center symmetry.
Connecting QDM with U(1) QLM
◮
The Hamiltonian of U(1) QLM:
i
Xh
† 2
†
) = H1 + H2 .
) − λ(U + U
J(U + U
H=−
H1
=
H2
=
H1
=
H2
=
◮
◮
Notice the first term and second term in the U(1) QLM flips a plaquette
2
and counts the number of flippable plaquettes (notice U
= 0),
respectively.
◮
In other words, the QLM and QDM have the same Hamiltonians, but
realize the corresponding Gauss law differently.
Connecting QDM with U(1) QLM
◮
QDM on the square lattice is characterized by the variables
Dxy ∈ {0, 1} which indicates the presence or absence of a dimer
on the link connecting neighboring sites x and y.
◮
The electric flux variables Exy are related to the dimer variables
Dxy by Exy = (−1)x1 +x2 (Dxy − 12 ).
Connecting QDM with U(1) QLM
◮
◮
GLM: Gx |ψi = 0.
P
Let Gx = i (Ex,x+î − Ex−î,x ) be the infinitesimal U(1) gauge
transformations (Gx commutes with the Hamiltonian). Then for
dimer covering constraint, namely each site is touched exactly by
one dimer, one has
X
(Dx,x+î + Dx−î,x ) = (−1)x1 +x2 .
Gx = (−1)x1 +x2
i
◮
This implies the dimer covering constraint is equivalent to a
staggered background electric charge ±1.
◮
Hence the physical states |Φi in the QDM should satisfy
Gx |Φi = (−1)x1 +x2 (Gauss law for QDM).
Controversial results of quantum dimer model on the
square lattice
plaquette
columnar
2.
3.
staggered
columnar
1.
columnar
staggered
staggered
mixed
0.0
0.6
1.0
λ
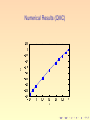
Numerical (Monte Carlo) Results
◮
We work with the height representation hX̃ of QDM living on the
(four) dual lattices x̃:
X̃ = (X1 +
◮
1
1
, X2 + ).
2
2
A
B
A
B
A
B
C
D
C
D
C
D
A
B
A
B
A
B
C
D
C
D
C
D
A
B
A
B
A
B
C
D
C
D
C
D
Numerical Monte Carlo Results
◮
The quantities hA,B,C,D , residing at the sites of a dual sublattice,
are related to the electric flux variables on the links by
◮
Ex,x+1̂
=
Ex,x+2̂
=
′
1
[hexX − hexX−2̂ ] mod2 = ± ,
2
′
1
(−1)x1 +x2 [hexX − hexX−1̂ ] mod2 = ± ,
2
X , X ′ ∈ {A, B, C, D}.
A
B
A
B
0
− 12
1
+ 21
C
D
C
D
+ 21
0
− 12
1
A
B
A
B
0
− 12
1
+ 21
C
D
C
D
+ 12
0
− 12
1
Numerical Monte Carlo Results
◮
◮
P
We introduce novel order parameters: MX = ex ∈X sexX hexX , with
1
1
sexA = sexC = (−1)(ex1 + 2 )/2 (xe1 + 21 even), sexB = sexD = (−1)(ex1 − 2 )/2
(xe1 + 12 odd)
With the order parameters
M11 = MA − MB − MC + MD = M1 cos ϕ1 ,
M22 = MA + MB − MC − MD = M1 sin ϕ1 ,
M12 = MA − MB − MC − MD = M2 cos ϕ2 ,
M21 = −MA + MB − MC − MD = M2 sin ϕ2 ,
◮
one defines ϕ = 12 (ϕ1 + ϕ2 + π4 ).
Columnar: ϕ = 0mod π4 ; plaquette: ϕ =
π
π
8 mod 4 .
Histograms of the Order parameters
❈ ✁✂✄☎❆✆
✓✕✕
✸
✹
✷ ✓✔✔
✶
✶
✷
✹
✸
✓✕✔
✷
✶
✸
✹
✹
✸ ✓✔✕
✷
✶
P✁❆✝✂✞✟✟✞
✓✕✕
❈ ❇
❆ ✓✔✔
❉
❆
❉
❇ ❈
✄▼✠✞❉
✓✕✕
✌✍ ✌☞ ☛☞ ☛✒
✎✍
✑✒ ✓✔✔
✑✏
✎✏
✑✏
✎✏
✎✍
✑✒
☛✒ ☛☞ ✌☞ ✌✍
✓✕✔
❉ ❈ ✓✔✕
❆
❇
❇
❆
❈ ❉
✓✕✔
✎✏ ✎✍ ✌✍ ✌☞ ✓
✑✏
☛☞ ✔✕
☛✒
✑✒
☛✒
✑✒
☛☞
✑✏
✌☞ ✌✍ ✎✍ ✎✏
❙✟❆✡✡✞✆✞❉
✓✕✕
❙
✓✔✔
✓✕✔
❙
✓✔✕
Histograms of the Order parameters
Figure : Left: λ = 0.8. Right: λ = 0.9.
Numerical Results (QMC)
✎
✮
❥
✍✌
☞☛
✡
❁
✂
✁✠
✁✟
✁✞
✁✝
✁✆
✁☎
✁✄
✁✥
✁✂
✲ ✁✂
▲✑✂✥✒❜❏ ✑ ☎
▲✑✥☎✒❜❏ ✑ ✟
▲✑✄✝✒❜❏ ✑ ✂✥
▲✑☎✟✒❜❏ ✑ ✟
▲✑✝ ✒❜❏ ✑ ✂✥
❞✏
✁✥
✁✄
✁☎
✁✆
✁✝
❧
✁✞
✁✟
✁✠
✂
Numerical Results (QMC)
✁ ☎
✲ ✁ ☎
✴✟❡
✲ ✁✝
✲ ✁✝☎
✲ ✁✆
✲ ✁✆☎
✲ ✁✄
✲ ✁✄☎
✲ ✁✂
✲ ✁✆
✁✆
✁✂
❧
✁✥
✁✞
✝
Numerical Results (Exact Diagonalization)
◮
Based on the angle ϕ as well as how it transforms under various
symmetries of the underlying model (QDM on the square lattice),
one can construct the corresponding low-energy effective theory.
◮
ρ 1
∂
ϕ∂
ϕ
+
∂
ϕ∂
ϕ
+ κ(∂i ∂i ϕ)2 + δ cos2 (4ϕ),
t
t
i
i
2 c2
which is identical with the effective Lagrangian of the
(2 + 1)-dimensional RP(1) model.
L=
◮
The rotor spectrum indicates that the columnar phase persists till
one reaches the RK point.
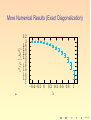
More Numerical Results (Exact Diagonalization)
c2 /ρ Ja2
3.2
3
2.8
2.6
2.4
2.2
2
1.8
1.6
1.4
1.2
1
−0.4−0.2 0
◮
0.2 0.4 0.6 0.8
λ
1
The phase diagram of QDM on the square lattice
◮
The columnar phase extends all the way to the RK point. No
mixed phase and plaquette phase are found.
More Numerical Results (QMC)
◮
Two external static charges ±2 relative to the staggered
background at two points separated by odd lattices spacings
− 21
1
+ 12
0
− 12
0
+ 21
0
− 21
0
+ 21
1
+ 12
0
+ 12
1
+ 12
0
− 21
1
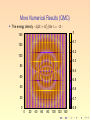
More Numerical Results (QMC)
◮
†
The energy density −J(U + U
) for λ = −2 :
140
0
-0.1
120
-0.2
100
-0.3
80
-0.4
60
-0.5
40
-0.6
20
-0.7
0
-0.8
0
20
40
60
80
100 120 140
More Numerical Results (QMC)
1
4
◮
The total flux 2 fractionalizes into 8 strands (each carries
◮
The interior of the strands displays plaquette order and represent
interfaces separating distinct columnar phases whose columns
are oriented in orthogonal directions.
0
140
-0.1
120
-0.2
100
-0.3
80
-0.4
60
-0.5
40
-0.6
20
-0.7
0
-0.8
0
20
40
60
80
100 120 140
flux).
More Numerical Results (QMC)
The energy of the string plays the role of a confining
charge-anti-charge potential V (r ) = σr
22
λ=-0.5
λ=0.5
λ=0.8
20
18
V(r)
◮
16
14
12
10
8
10
15
20
25
30
r
35
40
45
Conclusions
◮
The quantum dimer model(s) (QDMs) are introduced and the
possible candidate ground states for the model in the parameter
space λ/J are described.
◮
The U(1) quantum link model is introduced as well.
◮
Connection between QDM and U(1) QLM.
◮
We study the phase diagram of QDM on the square lattice by
simulating the U(1) QLM in the height variables space.
◮
No mixed and plaquette phases for λ ≤ 1.
◮
Fractionalized flux.