Download The Weak Interaction

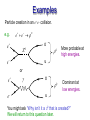
The Weak Interaction
The weak interaction can involve:
Baryons:
e.g. n  p  e   e
Mesons:
e.g. K    0  e   e
 0  
     
Leptons only:
e.g.    e   
e

Usually leptons are involved in the initial or final state – but not
always.
The Weak Interaction
The weak interaction is mediated by a gauge boson multiplet:
W, Z0, W+
Symbol in a
W j = 1 mass = 80.4 GeV/c2
Feynman
W+ j = 1 mass = 80.4 GeV/c2
diagram.
Z0
j = 1 mass = 91.2 GeV/c2
The large mass implies that the weak interaction has a very
short range.
It is therefore no wonder that it is “weak.”
Feynman Diagrams for Weak Interactions
e.g.  decay
p
e.g. + decay
n
p
n
W
e
e
W+
e+
e
Weak Interaction
Feynman Diagrams for Weak Interactions
e.g. EC
n
n
p
p
W+
e
W
or
e
e
e
Charge must be conserved at each vertex.
e.g. Muon decay
   e   e  


W+
e+
e
Weak Interaction
Feynman Diagrams for Weak Interactions
In terms of quarks:
(Quark flow diagram)
e.g.  decay
u
u
n
d
p
d
d
u


e
W
Q   13
e
Q   23
Therefore we see that a W or W+ must change the quark
flavor at the vertex in order to conserve charge.
Now we see why S  1 implies that the weak interaction is
involved, but S  0 does not imply that the weak interaction
is not involved.
Weak Interaction
Note that the quarks fall naturally into three generations:
First
Second
Third
Generation Generation Generation
Q   23
Q   13
u 
 
d 
c 
 
s 
t 
 
b 
Heavier
Heaviest
Light
This mirrors the three generations of Leptons.
Q0
Q  1
 e 
 
e 
  
 
 
  
 
 
A quark flavor change at a W boson vertex is most likely to
occur within a generation. (e.g. u  d, s  c, etc)
But cross generation changes are possible. (e.g. s  u)
Weak Interactions
Although a weak interaction vertex can link quarks of different
generations,
there are no weak interaction vertexes that cross lepton
generations.
i.e. there can be no vertexes like

e
e
W


Z0

Z0
e
This rule is equivalent to saying that all the lepton numbers,
Le, L and L must be conserved at each vertex.
Strong Interaction
The Strong interaction is mediated by a single gauge boson.
Gluon: g
Symbol in a
Mass = 0
Feynman
Charge = 0
diagram.
Spin = 1
The fact that the gluon has zero mass means that the strong
force has a long range.
But: Quark confinement means that the manifestation of the
force between hadrons is a short range force.
e.g. The N-N interaction is mediated by pions.
The theory of the strong interaction is Quantum
Chromodynamics (QCD).
Strong Interaction
Gluons act only on quarks (not leptons).
(Leptons cannot carry colour charge.)
Gluons cannot change the flavor of a quark.
A Feynman diagram can only contain two types of
quark-gluon vertexes.
q
q
q
or
g
q
g
Strong Interaction
e.g. The exchange of a virtual pion between two protons.
p
0
p
p
p
p
d
u
d
u
u
u
0 u
This is just one
example for this
pion exchange
interaction
u
u
p
u
u
d
u
d
Strong Interaction
In the Electromagnetic interaction
the photons couple to charges
and the photon carries no charge.
But in the Strong interaction
gluons couple to colour charges (RGB)
and the gluon carries colour information.
e.g.
R
B
q
q
In this case the gluon
carries colour
g
RB
information:
B
R q
q
In general, a gluon changes the colour of a quark at a vertex.
Strong Interaction
In principle, there are nine possible gluon species.
RR RB RG BR BB BG GR GB GG
However this does not describe our world.
QCD is based on a colour symmetry (SU(3) in group theory)
that results in
a colour octet:
( R B  BR )
5 
i
2
( RG  GR )
i
2
( R B  BR )
6 
1
2
( BG  GB )
3 
1
2
( RR  B B )
7 
i
2
( BG  G B )
4 
1
2
( RG  GR )
8 
1
6
( RR  B B  2 G G )
1 
1
2
2 
and a colour singlet:
9 
1
3
( RR  BB  GG )
Strong Interaction
Since the gluon is massless the range of the gluon is infinite.
But we have said that all real particles are colour singlets
(colour charge zero).
Therefore if a gluon is to be exchanged between two particles
(e.g. a neutron and a proton)
the gluon must be also be a colour singlet (i.e. does not
carry colour).
In that case it would have to be the colour singlet gluon.
9 
1
3
( RR  BB  GG )
But the evidence of our observation of the real world is that
gluons are not seen.
Therefore, our world includes only the other eight gluons.
These gluons cannot be seen as free particles since, if they
leave a particle, they would leave behind a particle that is
not colour neutral.
Strong Interaction
Looking again at a quark-gluon vertex, we can deduce the
colour charges carried by the gluon.
q
R
B
q
g
q B
R
In the top vertex:
q
R  Bg
I 3c : 12  0  I 3c (g)  I 3c (g)  12
Yc :
1
3
  23  Y c (g)  Y c (g)  1
i.e. the colour charges carried by the gluon are not zero.
Strong Interaction
The disturbing part of the gluons is that, because they carry
colour charge, they can interact with each other!
e.g. we can have vertexes like:
RB
RG
BG
This severely complicates calculations in QCD.
In Quantum Electrodynamics (QED) the photons do not
carry charge, so the photons do not interact with each
other.
Strong Interaction
In a proton, for example, there are gluon exchanges occurring
all the time.
G
R u
e.g.
u R
RG B
GR B
G
p
u
u
p
R BR
B
R
G d
d
When we draw quark-level Feynman diagrams, we
generally do not show the gluons since this would get too
tedious and messy.
Sometimes, such diagrams are referred to as Quark flow
diagrams.
Strong Interaction
p      0  
e.g.
p


u
u
d
u
u
u
 
d
u
u
u
0
Note: Although the quark flavors have changed, this
does not mean that the weak interaction needs to be
involved.
The total quark content in the initial and final state is the
same.
Initial: uud  du  uuu
Final: uuu  uu  uuu
Strong Interaction
p      0  
e.g.
Another possible mechanism for this reaction is:
p


u
u
d
u
u
u
 
d
d
u
d
0
Note that the 0 can be in the uu or dd state since
formally it is a superposition of both.
This would still be a strong interaction reaction since
gluons must be exchanged.
Examples
Some examples of reactions and decays in terms of quarks.
e.g. decay of
D0  K    
Quark content: cu
su u d
Quark flow diagram.
c
W+
D0
Flavors in the initial and final
state are different.
Therefore the weak
interaction must be involved.
s
u
u
u
d
K

Note: In this case flavor changes stay within a quark generation.
Note: The strong interaction can be involved as well to
create the quark-antiquark pair.
Examples
e.g. decay of
D 0  K   e   e
cu
su
u
u
c
s
D0
W+
K
e
e
Note: No strong interaction needs to be involved.
Note: This is just beta-decay with a charmed hadron.
Examples
The W boson can create quark-antiquark pairs of
different flavors.
e.g.
D  K 0   
cd
D

s d ud
d
d
c
s
W+
d
u
Q : 1   13  23
K0

Examples
An example of generation mixing.
K      
e.g.
su
s
K
W
u


or
W
e
e
etc.
Examples
Examples involving the electromagnetic interaction.
e.g.   p  
u
d
u


J 
u
d
u
3
2

J 
p
1
2
The photon flips the spin of one quark.
The photon carried away angular momentum with L  1, or 2
Parity change  = +1. Therefore photon was M1 or E2
Examples
e.g.  0    

u

0
u
u
u
Not

u
The two photons are necessary to conserve, energy,
momentum and angular momentum.
e.g. Angular momentum: Pion spin s = 0 (and L = 0)
Minimum photon L = 1
Therefore there must be at least 2 photons so that final
angular momentum can couple to zero.

Examples
Interactions involving the Z0 boson.
e.g.
e
e   e    e  e
Z
0
e
e
e
Weak interaction.
However, when there is an e+e


collision, the EM process e  e    
will be the dominant result.
Examples
Particle creation in an e+e collision.
e.g.
e  e   0
e
Z0
e
u

0
More probable at
high energies.
u
or
e
e

u
0
Dominant at
low energies.
u
You might ask “Why isn’t it a 0 that is created?”
We will return to this question later.
Electroweak Interaction
We will just mention here that the unification of the
EM and Weak interactions involves a unification of
the photon and the W and Z particles.
High Energies

Low Energies
4 massless gauge bosons
Singlet:
Triplet:
Q0

Q  e
W
Q0
Q  e

Z0
W
Remains massless
Acquire mass
Vertex Rules
A summary of the conservation laws at vertexes.
g
Lepton  neutrino Quark
change
flavor
change
No Interaction
No
Quark
colour
change
Yes
EM

No
No
No
Weak
W +
Z0
Yes
No
Yes
No
No
No
Interaction
Boson
Strong
e.g.

e
e


Z
0
e
e
W
e

e