Download Interactive Study Guide for Students: Trigonometric Functions

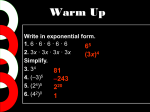
Chapter 4: Factors and Fractions
Section 1: Factors and Monomials
Find Factors
Examples
Two or more numbers that are multiplied to form a product are
called _________________.
1. Determine whether 138 is
divisible by 2, 3, 5, 6, or 10.
4  9 = 36
factors
product
So, 4 and 9 are factors of 36 because they each divide 36 with a
remainder of 0. We can say that 36 is ____________ by 4 and 9.
Divisibility Rules - A number is divisible by:

2 if the ones digit is divisible by 2 __________

3 if the sum of its digits is divisible by 3 _________

5 if the ones digit is 0 or 5 __________

6 if the number is divisible by 2 and 3 __________

10 if the ones digit is 0
2. There are 192 guests at a
party. Should you choose
tables that seat 5, 6, or 10 if
you want all the tables to be
full?
3. Use the table to list all of
the factors of 72.
#
divide
factors
1
72/1=72 1  72
___________
Monomials
A number such as 80 or an expression such as 8x is called a
____________________. They are numbers, variable, or a product
of numbers and/or variables.
Monomials
Not Monomials
4
A number
2+x
2 terms added
y
A variable
5c - 6
2 terms subtracted
-2rs
A product
3(a+b)
2 terms added
Interactive Study Guide for Students: Pre-Algebra
_ _ _ _ _ _ _ __ __ __ __ __ __
Determine whether each
expression is a monomial: 4.
2(x – 3)
5. -48xyz
Chapter 4: Factors and Fractions
Section 2: Powers and Exponents
Powers and Exponents
Examples
An expression like 2222 can be written as a __________. A power Write each expression using
has two parts, a _________ and an ______________. An exponent is a exponents.
shorter way of writing repeated multiplication. So 2222 can be
1. 3333333 = ____
written 24.
Powers
Words
Repeated Factors
21
2 to the first power
2
22
2 to the second power
22
23
2 to the third power
222
24
2 to the fourth power
2222
2n
2 to the nth power
222…2 n factors
2. ttttt = ____
3. (-9)(-9) = _____
4. (x+1)(x+1)(x+1) = _____
5. 7aaabb = _____
6. Express 13, 048 in
expanded form.
Any number, except zero, raised to the zero power is defined to be
________.10=___ 20=___ 30=___ x0=___, x≠0
A number is in _____________ form if it does not contain exponents.
You can use place value and exponents to express a number in
____________ form.
Standard form: 256 Expanded form:(2100) +(510) + (61)
=
= (2x102) + (5x101) + (6x100)
Evaluate Expressions
Remember ____________ comes after parenthesis in the
___________ or operations.
Simplify expressions inside
grouping symbols.
(3 + 4)2 + 5  2 = 72 + 5  2
Evaluate all powers
= 49 + 5  2
Mult. and Div. from left to right
= 49 + 10
Add and Subtract from left to
right
= 59
Interactive Study Guide for Students: Pre-Algebra
Evaluate each expression 7.
23 = ____
8. y2 + 5 if y=-3
9. 3(x + y)4 if x=-2 y=1
Chapter 4: Factors and Fractions
Section 3: Prime Factorization
Prime Numbers and Composite Numbers
Examples
A whole number that has exactly two factors, 1 and itself, is called a
_____________ number. A whole number that has more than two
factors is called ________________. Zero and one are neither prime
nor composite.
Whole numbers
Factors
Number of Factors
0
All numbers
Infinite
1
1
1
2
1, 2
2
3
1, 3
2
4
1, 2, 4
3
5
1, 5
2
1. Is 19 prime? Why?
2. Is 28 prime? Why?
When a composite number is expressed as the product of prime
factors, it is called the _____________ ______________. Two ways to
find the prime factorization of a number is to use a _______________
tree or the _________ method.
Factor tree
Cake method
Factor each monomial:
Factor Monomials
3. 8ab3
To _____________ a number means to write it as a _______________
of its factors. A monomial can also be factored as a product of prime
numbers and variables with no exponent greater than 1. Negative
coefficients can be factored using -1 as a factor.
Interactive Study Guide for Students: Pre-Algebra
Chapter 4: Factors and Fractions
4. -30x4y
Section 4: Greatest Common Factor (GCF)
Greatest Common Factor
Often, numbers have some of the same factors. The greatest number
that is a factor of two or more numbers is call the _______________
____________ ____________ (GCF). There are two ways to find
them:
Examples
Find the GCF of each set of
numbers.
1. 30, 24
_________ all factors, find the biggest one in common:
2. 54, 36, 45
12:
20:
Use ___________ factorization:
12:
20:
3. A track team has 208 boys
and 240 girls. What is the
greatest number of teams
that can be formed & have
same number of girls and
boys? How many of each will
be on the team?
Factor Algebraic Expressions
You can also find the GCF of two or more monomials by finding the
_________ of their common ________ __________.
Example:
4. Find the GCF of 16xy2 and
30xy.
30a3b2 :
24a2b:
5. Factor 2x + 6
When you find the GCF of the two monomials, then you can do the
______________ of the distribution property and factor out the GCF.
Example:
4x + 16 =
6. Factor 3y - 12
Interactive Study Guide for Students: Pre-Algebra
Chapter 4: Factors and Fractions
Section 5: Simplifying Algebraic Equations
Simplify Numerical Fractions
A fraction is in _______________ form when the GCF of the
numerator and the denominator is 1. One way to write a fraction is
simplest form is to write the prime factorization of the numerator and
the denominator, the divide the numerator and denominator by the
___ ___ ___.
Examples
Write each fraction in
simplest form.
1.
9
12
2.
15
60
3. Eighty Eight feet is what
part of a mile?
Simplify Algebraic Fractions
A fraction with variables in the numerator or the denominator is
called an _____________ ___________. They should also be written
in ________________ form.
Simplify:
21x 2 y
4.
35 xy
Example:
25 xy 2
=
75 x 2 y
5.
6r
15rs
6.
abc 3
a 2b
Interactive Study Guide for Students: Pre-Algebra
Chapter 4: Factors and Fractions
Section 6: Multiplying and Dividing Monomials
Multiplying Monomials
Examples
Remember that exponents are used to show repeated multiplication.
You can use that to understand how to ___________ numbers with
the same base.
Example: 2 2 = (223)(2222) = 2
3
4
1. 7  74 =
2. x5x2 =
7
You can multiply powers with the _______ ________ by
_____________ their exponents.
3. (-4n3)(2n6)
am  an = am+n
32  34 = 32+4 = 36
Divide Monomials
57
4. 4
5
You can also find out how to divide powers.
26
22
=
222222
= 24
22
You can divide powers with the same base by subtracting their
exponents.
am
an
26
22
=
=
a mn
2 62
where
5.
y5
y3
a0
= 24
Interactive Study Guide for Students: Pre-Algebra
Chapter 4: Factors and Fractions
6. The processing speed of
computers in 1993 was 108
instructions per second. In
1999, it was 109 inst/sec. How
much faster did they become?
Section 7: Negative Exponents
Negative Exponents
Examples
Write each expression using a
positive exponent 1. 6-2
Finish this table:
Power
Value
26
64
25
32
24
16
23
8
2. x-5
1
3. Write as an expression
9
using a negative
exponent.
22
4. A Hydrogen atom (H) is
only 0.00000001cm in
diameter. Write the decimal
as a fraction and as a power of
ten.
21
20
2-1
2-2
So 2-1 can be defined as
1
. You can apply the Quotient of Powers
2
rule and the definition of a power to
x3
and write a general rule
x5
about negative powers.
x3
= x3-5 = x-2
x5
x3
x5
=
xxx
1
= 2
xxxxx
x
So x-2 =
1
1
and a  n  n
2
x
a
5. Evaluate x-3 if x = 3
Evaluate Expressions
Algebraic expressions containing negative exponents can be written
using ____________ exponents and evaluated.
Example: Evaluate n-3 if n=2. 2-3 =
6. Evaluate 3-x if x = 2
1 1
=
23 8
Interactive Study Guide for Students: Pre-Algebra
Chapter 4: Factors and Fractions
Section 8: Scientific Notation
Scientific Notation
Examples
When you deal with very large numbers, such as the distance to the
moon, or very small numbers, such as the size of an atom, it is difficult
to keep track of the place value. Numbers like these can be written in
_______________ ________________.
Express each number in
standard form.
A number is in scientific notation when it is written as the
___________ of a ______and a _____ of __. The factor must be
greater that or equal to 1 and less than 10 (or in other words, only
____ digit in front of the decimal).
2. 5.1 x 10-5
Example: 5,200,000,000 = 5.2 x 109
0.000000034=3.4 x 10-8
1. 3.78 x 106
Express each number in
scientific notation.
3. 60,000,000
4. 32,800
Compare and Order Numbers
To compare and order numbers in scientific notation, first compare
the ___________. The number with the greater exponent is greater.
If the exponents are the same, compare the factors. The greater
factor is the greater number.
Planet
Distance from Sun
Mercury
5.80 x 107
Venus
1.03 x 108
Earth
1.55 x 108
Mars
2.28 x 108
Jupiter
7.78 x 108
Saturn
1.43 x 10
9
Uranus
2.87 x 109
Neptune
4.50 x 109
Pluto?
5.90 x 109
5. 0.0048
Use the table at the left to
answer the questions
6. Light travels at
300,000km/sec. Estimate
how long it takes light to
travel from the sun to the
Earth. (remember d = rt)
7. Order Mars, Jupiter,
Mercury and Saturn from
least to greatest distance
from the Sun.