Download The Two Characteristics of Superconductivity

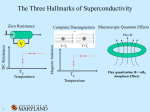
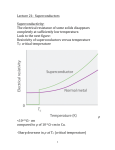
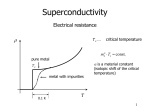
Lecture 21: Superconductors
Superconductivity:
The electrical resistance of some solids disappears
completely at sufficiently low temperature.
Look to the next figure:
Resistivity of superconductors versus temperature
TC: critical temperature
<10-23 Ω ∙ cm
compared to 𝜌 of 10-9 Ω ∙cm in Cu.
-Sharp decrease in 𝜌 at TC (critical temperature)
1
𝜌
-Metallic elements:
TC:
Hg 4.15K
W 0.01 K
Nb 9.3K
-Metal oxides (Ceramics):
High temperature semiconductors
YBaCuO7 HgCuo (contain CuO2 or NiO2).
-Cu, Ag, Au, … or Fe, Ni, Co are not superconductors
The Two Characteristics of Superconductivity:
 The absence of resistance to current flow
 Exclusion of magnetic flux (Meissner effect)
Meissner Effect
As a superconducting substance is cooled below its
critical temperature in the presence of applied magnetic
field, it expels all magnetic flux from its interior.
2
Ill explain in more detail
This leads to a very interesting phenomena (magnetic
levitation)
3
A permanent magnet floating over a superconducting
surface
-magnetic train
Let’s go back to the previous figure:
4
Now, if the external magnetic field increases beyond a
certain value (the critical field HC) the material ceases to
be superconductor and becomes normal.
-If the temperature increases beyond TC, the material
becomes normal.
Thus, there is a critical temperature, critical magnetic
field, and critical current.
5
-Critical temperature, critical magnetic field, critical
current
Let’s look again to (H-T) curve:
HC: critical magnetic field
Above HC, the superconductivity is destroyed
𝐻𝐶 = 𝐻0 (1 −
A: normal state
Magnetic field=zero
6
𝑇2
𝑇𝐶
2)
Path: ABCD
Cooling down:( A⟶B)
B: superconductor
H: still zero
C: Turn in magnetic field, changing flux creates electric
field that sets up a current that opposes magnetic field
(Lenz law).
Since there is no resistivity, eddy currents don’t decay
but create magnetic field that cancels the applied field.
Superconductors act as perfect diamagnet
We can summarize:
Now, let’s go through the path ADCB: i.e. apply a field to
a normal state, then cool down. What happened?
7
It expelled the magnetic field. We call the two cases
Meissner effect: generated field exactly cancels out the
applied field in superconductor
What is Behind Superconductivity
Before I give some explanation for the phenomena, let
me remind you what we have so far:
 Classical theory of metallic conduction treated
electrons as a gas of independent particles.
 Quantum Mechanics: treated electrons as
independent particles, and took into account the
wave nature of electrons and exclusion principle.
 Fermi distribution
 Quantization of energy level and band
theory of solids
Independent particles failed to explain
superconductivity. We need many-body effects
There was an obvious experimental evidence for the
need of many-body effects.
Experimental Evidence:
Isotope effect: The critical temperature of a
superconductor depends on the total mass of the
nucleus
1
𝑇𝐶 ∝
√𝑀
if we use the isotope, (this means we add more
neutrons) the critical temperature decreases. This
8
suggests that the lattice vibrations play a role in
superconductivity.
We must take into account:
 electron-phonon interaction
 electron-electron interaction
BCS Theory (Bardeen, Cooper, Schrieffer, 1957) takes
that into account.
Although thermal vibrations are behind the resistivity,
in some materials and below a certain temperature, the
lattice vibrations play a role as an intermediate between
two electrons. It results in an attractive force between
the two electrons.
9
The first electron deforms the lattice. The second
electron is attracted by the deformation (region of
increased positive charge density).
The first electron has emitted a phonon. A second
electron passing by the region will absorb the phonon.
The two electrons have exchanged momentum with
each other.
Attractive interaction exceeds repulsive interaction. The
two electrons are weakly bound and form Cooper pair.
Cooper pairs are responsible for superconductivity.
10
11
-What are the conditions for superconductivity?
1.
2.
3.
4.
12
 According to BCS theory, the binding energy of a
cooper pair at absolute zero is about 3kbTC , where
kb is Boltzmann constant, TC is critical temperature
 Cooper pairs do not obey Fermi-Dirac statistics.
They are bosons.
 BCS theory presently fails to explain
superconductivity of high temperature super
conductors
Summary of Superconductor Properties:
 They behave as (no DC resistors)
 They behave as a perfect dimagnet and experience
“Meissner” effect
 A band gap was implied by the very fact that the
resistance is precisely zero. If charge carriers can
move through a crystal lattice without interacting
at all, it must be because their energies are
quantized such that they do not have any available
energy levels within reach of the energies of
interaction with the lattice.
 Energy gap
13
The lower energy of superconductivity electrons
are separated from the normal state by energy gap
about EF
Classification of Superconductors:
Type I (soft)
Type II (hard)
-Type I superconductors:
most superconductive elements except Nb
14
Superconductivity is destroyed by applying a small
magnetic field HC
-Type II superconductors:
The elimination of superconductivity state is gradually
15
It has
mixed (vortex) state
Less than Hc 1→ superconductor
Above HC 2 → normal
There are intermediate fields, where material has both
normal and superconductor regions
16
Type II includes:
- Nb
- All alloys
Note: Type II have higher TC, higher HC and higher IC
17
𝑐
𝜙0 = ℎ 2𝑒 = 2.07 𝑥 10−7 𝑔𝑎𝑢𝑠𝑠 − 𝑐𝑚2 known as a
fluxoid or flux quantum.
18
19
20