Download Transverse Electromagnetic Waves in Free Space

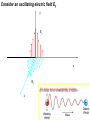
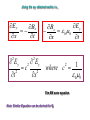
Transverse Electromagnetic
Waves in Free Space
“Let there be electricity and magnetism
and there is light”
J.C. Maxwell
What we know from previous classes?
1) Oscillating magnetic field generates electric
field (Faraday´s law) and vice-versa (modified
Ampere´s Law).
2) Reciprocal production of electric and magnetic
fields leads to the propogation of EM waves
with the speed of light.
Question: WAVES?????? How do we show
that a wave is obtained?
Aim of class today:
To derive the EM wave equation
Consider an oscillating electric field Ey
y
Ey
x
Bz
If a charge moves non-uniformly, it radiates
z
Y
This will generate a magnetic
field along the z-axis
Ey(x)
Ey(x+x)
C
Z
x
We know that Faraday´s law in the integral form in given as:

 E.dl    B.ds
t
C
s
where C is the rectangle in the XY plane of length l width x, and S is the open
surface spanning the contour C
Faraday´s law on the contour C


Bz
E y ( x  x)  E ( x) l  
l x
t
this implies...
E y
Bz

x
t
Keep this is mind...
Ampere´s law with displacement current term

 B.dl     E.ds
t
o
C
o
Y
x
Ey
By(x)
x
C/
z
s
By(x+x)
Ampere´s law, for the Contour C/
 Bz ( x  x)  Bz ( x)l   0 0
E y
t
this implies...
E y
Bz

  0 0
x
t
lx
Using the eq. obtained earlier i.e.,
E y
E y
Bz

  0 0
x
t
Bz

x
t
 Ey
2
t
2
 Ey
2
c
2
x
2
where
c 
2
The EM wave equation
Note: Similar Equation can be derived for Bz
1
 0 0
Electromagnetic waves
for E field
for B field
In general,
electromagnetic waves

1
  2 2
c t
Where  represents E or B
2
2
or their components
1. FEYNMAN LECTURES ON PHYSICS VOL I
Author : RICHARD P FEYNMAN,
IIT KGP Central Library
Class no. 530.4
2. OPTICS
Author: EUGENE HECHT
IIT KGP Central Library
Class no. 535/Hec/O