* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Fluid Dynamics
Lattice Boltzmann methods wikipedia , lookup
Ballistic coefficient wikipedia , lookup
Airy wave theory wikipedia , lookup
Accretion disk wikipedia , lookup
Compressible flow wikipedia , lookup
Boundary layer wikipedia , lookup
Sir George Stokes, 1st Baronet wikipedia , lookup
Magnetohydrodynamics wikipedia , lookup
Hemodynamics wikipedia , lookup
Flow measurement wikipedia , lookup
Flow conditioning wikipedia , lookup
Lift (force) wikipedia , lookup
Wind-turbine aerodynamics wikipedia , lookup
Hemorheology wikipedia , lookup
Computational fluid dynamics wikipedia , lookup
Hydraulic machinery wikipedia , lookup
Drag (physics) wikipedia , lookup
Navier–Stokes equations wikipedia , lookup
Coandă effect wikipedia , lookup
Bernoulli's principle wikipedia , lookup
Aerodynamics wikipedia , lookup
Derivation of the Navier–Stokes equations wikipedia , lookup
Fluid thread breakup wikipedia , lookup
Reynolds number wikipedia , lookup
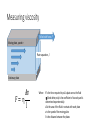
Fluid Dynamics Viscosity, Poiseuille’s Equation, Coanda Effect From ideal fluids to real fluids So far, we have considered ideal fluids: • They coast along with no difference in pressure • An ideal milk shake would be as easy to drink as a watery soda • The primary difference between ideal fluids and real fluids is their viscosity. Viscosity Honey and water have almost identical densities, but their flow properties are dramatically different. Viscosity: measure of a fluid’s resistance to flow blood flow flight curve ball Factors that affect flow of fluids • Pressure difference • How hard is fluid being pushed forward minus how hard fluid is being pushed back • Radius of tube • Harder to push fluids through narrower tubes • Length of tube • Longer tubes offers more resistance • Viscosity of fluid • Water flows more easily than molasses Measuring viscosity Pulled with force F Moving plate, speed v Plate separation, l Stationary plate 𝐴𝑣 𝐹= 𝑙 Where F is the force required to pull a plate across the fluid (Greek letter, eta) is the coefficient of viscosity and is determined experimentally. A is the area of the fluid in contact with each plate v is the speed of the moving plate l is the distance between the plates Coefficient of viscosity Fluid Coefficient of viscosity, , varies for different substances = 𝐹𝑙 𝑣𝐴 Units of 𝑁𝑚 𝑚 𝑠 𝑚2 = 𝑁 𝑚 2 𝑠 = 𝑃𝑎 ∙ 𝑠 (Ps) Air (20C) 1.8x10-5 Water (20C) 1.0x10-3 Water (40C) 0.7*10-3 Water (60C) 0.5*10-3 Blood (37C) 2.5*10-3 Motor oil (-30C) 3.0*105 Motor oil (40C) 0.07 Motor oil (100C) 0.01 Honey (15C) 600 Honey (40C) 20 For situations with laminar flow, Poiseuille’s equation 𝑉 𝜋𝑅4 𝑃1 − 𝑃2 = 𝑡 8𝑙 The flow rate is proportional to… • the radius of the tube (to the 4th power!) • pressure difference The flow rate is inversely proportional to… • the length of the tube • the coefficient of viscosity Turbulent flow The onset of turbulence occurs when the Reynolds number, Re >2000. Reynolds number is defined as 2𝑣𝑎𝑣𝑒𝑟𝜌 𝑅𝑒 = Where vave is the average speed of the fluid r is the radius of the tube through with the fluid is flowing is the density of the fluid is the coefficient of viscosity of the fluid Solids traveling through viscous fluids • Lift • Coandă Effect http://en.wikipedia.org/wiki/Coand%C4%83_effect • Demo: cylindrical object in stream of water • Coanda planes, proof of concept physics Lift • When air passes over a wing, viscosity of air creates “downwash” • Coandă effect creates a boundary layer next to surface of wing • A change in direction requires a force. • If the wing exerts a downward force on air, then air exerts an upward force on wing. Drag 1 𝐹𝑑𝑟𝑎𝑔 = 𝐶𝐷𝜌𝐴𝑣2 2 where CD is the dimensionless number related to shape is the density of the fluid A is the cross-sectional area exposed to fluid v is the speed of the solid through the fluid Example Estimate the drag on a car traveling at 27 m/s (60 mph). Assume the drag coefficient for a well-designed car is 0.5, air = 1.3 kg/m3, and the frontal area of the car is 3.0 m2. G v= 27 𝑚/𝑠 𝜌𝑎𝑖𝑟 = 1.3 𝑘𝑔/𝑚3 U E Fdrag=? CD=0.5 A = 3.0 m2 1 𝐹𝑑𝑟𝑎𝑔 = 𝐶𝐷𝜌𝐴𝑣2 2 S 1 𝐹𝑑𝑟𝑎𝑔 = 0.5 2 S 𝐹𝑑𝑟𝑎𝑔 = 180 𝑁 𝑘𝑔 1.3 3 𝑚 3.0 𝑚2 27 𝑚 𝑠 2 For more experimentally determined values of coefficient of drag, check Engineering Toolbox and Wikipedia (yea, science nerds!) Example Estimate the terminal velocity of a 60-kg skydiver who has a surface area of 1.5 m2 and an assumed CD of 0.6. G 𝑚 = 60 𝑘𝑔 𝜌𝑎𝑖𝑟 = 1.3 𝑘𝑔/𝑚3 U E 𝑣𝑡𝑒𝑟𝑚𝑖𝑛𝑎𝑙 =? CD=0.6 A = 1.5 m2 Terminal velocity = no acceleration, therefore Fweight = Fdrag, 1 Where 𝐹𝑑𝑟𝑎𝑔 = 2 𝐶𝐷𝜌𝐴𝑣2 and 𝐹𝑤𝑒𝑖𝑔ℎ𝑡 = 𝑚𝑔 1 So 2 𝐶𝐷𝜌𝐴𝑣2 = 𝑚𝑔 So 𝑣 = S S 2𝑚𝑔/(𝐶𝐷𝜌𝐴) 𝑣𝑡𝑒𝑟𝑚𝑖𝑛𝑎𝑙 = 2 60 𝑘𝑔 0.6 𝑣𝑡𝑒𝑟𝑚𝑖𝑛𝑎𝑙 = 55 𝑚/𝑠 𝑚 9.8 𝑠2 𝑘𝑔 1.3 𝑚3 (1.5𝑚2)