* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download The TESLA Accelerator and Linear Collider
Introduction to gauge theory wikipedia , lookup
Nordström's theory of gravitation wikipedia , lookup
Woodward effect wikipedia , lookup
Old quantum theory wikipedia , lookup
Casimir effect wikipedia , lookup
Path integral formulation wikipedia , lookup
Quantum vacuum thruster wikipedia , lookup
Renormalization wikipedia , lookup
Photon polarization wikipedia , lookup
Electromagnetism wikipedia , lookup
Quantum electrodynamics wikipedia , lookup
Mathematical formulation of the Standard Model wikipedia , lookup
Aharonov–Bohm effect wikipedia , lookup
Field (physics) wikipedia , lookup
History of quantum field theory wikipedia , lookup
Time in physics wikipedia , lookup
Relativistic quantum mechanics wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
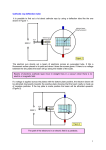
An Introduction to the Physics and Technology of e+e- Linear Colliders Lecture 7: Beam-Beam Effects Nick Walker (DESY) DESY Summer thStudent Lecture th USPAS, Santa Barbara, 16 -27 2003 31st June, July 2002 Introduction • Beam-beam interaction in a linear collider is basically the same Coulomb interaction as in a storage ring collider. But: – Interaction occurs only once for each bunch (single pass); hence very large bunch deformations permissible. – Extremely high charge densities at IP lead to very intense fields; hence quantum behaviour becomes important • Consequently, can divide LC beam-beam phenomena into two categories: – classical – quantum Introduction (continued) • Beam-Beam Effects – – – – – – Electric field from a “flat” charge bunch Equation of motion of an electron in flat bunch The Disruption Parameter (Dy) Crossing Angle and Kink Instability Beamstrahlung Pair production (background) Ebeam bx by sx sy sz Ne GeV mm mm nm nm mm 1010 NLC 250 8 0.1 245 2.7 110 0.75 TESLA 250 14 0.4 550 5 300 2.0 CLIC 1500 8 0.15 43 1 30 0.42 Storage Ring Collider Comparison Linear beam-beam tune shift x, y b x, y re Nb 2 s x , y (s x s y ) Putting in some typical numbers (see previous table) gives: x 0.54 y 1.44 Storage ring colliders try to keep x , y 0.05 Electric Field from a Relativistic Flat Beam • Highly relativistic beam E+vB 2E • Flat beam sx sy (cf Beamstrahlung) • Assume • infinitely wide beam with constant density per unit length in x ( r(x)) • Gaussian charge distribution in y: • for now, leave r(z) unspecified 2 1 1 y r ( y) exp 2 s y 2s y r ( x) 1 2s x Electric Field from a Relativistic Flat Beam Use Gauss’ theorem: q E ds s E y ( y, z )xz 0 qN r ( x) r ( z )xz 0 y r ( y ')dy ' y ' 0 y qN E y ( y, z ) Erf r ( z) 2 2 0s x 2 s y Assuming Gaussian distribution for z, the peak field is given by Eˆ y qN 4 0s xs z Electric Field from a Relativistic Flat Beam E y MV/cm s x 500 nm s y 5 nm 2000 s z 300 μm 1000 N 1010 10 5 5 1000 2000 Note: 2Ey plotted Assuming a Gaussian distribution for r(z) z 0 10 y /s y Electric Field from a Relativistic Flat Beam s x 500 nm s y 5 nm s z 300 μm N 1010 E y MV/cm 1500 1000 effect of x width 500 z 0 10 20 Assuming a Gaussian distribution for r(z) 30 40 50 y /s y Equation Of Motion F = ma: y (t ) 2qE y ( y, t ) m0 y(t ) c 2 y( z ) Changing variable to z: y( z ) 2qE y ( y, z ) m0c 2 y( z) q N Erf r (2 z ) 2s z y 2 0s x mo c 2 2 q2 re 4 0 m0c 2 y( z ) 2 2 Nre sx y( z) Erf r (2 z ) 2s z y why rz(2z)? Linear Approximation and the Disruption Parameter Taking only the linear part of the electric field: y( z ) 4 Nre r (2 z ) s xs y y( z) k2 (z) Take ‘weak’ approximation: y(z) does not change during interaction y(z) = y0 Thin-lens focal length: y 4 Nre s xs y y0 r z (2 z )dz 2 Nre 1 y0 y0 s xs y f 2 Nre 1 f s xs y Define Vertical Disruption Parameter 2 Nres z s Dy z f s xs y exact: Dy 2 Nres z s x s y s y Number of Oscillations Equation of motion re-visited: 2 Dy y( z ) r z (2 z ) y( z ) sz Approximate r(z) by rectangular distribution with same RMS as equivalent Gaussian distribution (sz) half-length! Dy y( z ) 0.4 1 2 3s z 0.3 k 2 0.2 0.1 3s Dy 3s z2 2 z y( z ); 3 z sy 2 3ks z 2 1 0 3 2 3s z 1 0 1 2 3s z 3 3 4 Dy 2 0.21 Dy Example of Numerical Solution N 2 10 s x 500 nm 10 s y 5 nm s z 300 μm E 250 GeV Dy 27.7 1.1 y / nm 40 green: rectangular approximation 20 0 20 black: gaussian 40 500 0 z ( ct )/ μm 500 1000 1500 Pinch Enhancement • Self-focusing (pinch) leads to higher luminosity for a head-on collision. H Dx , y 3 D x, y 1/ 4 1 Dx , y ln 1 D3 x, y Dx , y 0.8b x , y 1 2 ln sz ‘hour glass’ effect Empirical fit to beam-beam simulation results Only a function of disruption parameter Dx,y 3 3 2 2 1 1 Y Y The Luminosity Issue: Hour-Glass 0 0 1 1 2 2 3 3 2 1 0 Z 1 b = “depth of focus” reasonable lower limit for b is bunch length sz 2 2 1 0 Z 1 2 Luminosity as a function of by L (cm2s1) 34 5 10 BS s1 s z 100m m z 34 4 10 34 s z 300m m 2 1034 500m m 3 10 nb N 2 f L 4s xs y 700m m 900m m 1 1034 200 400 600 b y (m m) 800 1000 Beating the hour glass effect Travelling focus (Balakin) • Arrange for finite chromaticity at IP (how?) • Create z-correlated energy spread along the bunch (how?) s z b y* Beating the hour glass effect Travelling focus • Arrange for finite chromaticity at IP (how?) • Create z-correlated energy spread along the bunch (how?) s z b y* Beating the hour glass effect Travelling focus • Arrange for finite chromaticity at IP (how?) • Create z-correlated energy spread along the bunch (how?) ct Beating the hour glass effect foci ‘travel’ from z = 0 to z = 3s z chromaticity: 3s z 3s z f y y travelling focus: t=0 3s z 2ct NB: z correlated! RMS f = ct t>0 sz 2 y 2 z 2 y RMS s z2 2 y 1 2 3 6 4 5 The arrow shows position of focus for the read beam during travelling focus collision Kink Instability Simple model: ‘sheet’ beams with: r x, z 1 2 3s x , z Linear equation of motion becomes 2 Dy y( z ) y ( z ); 2 6 sz 3 z sz 2 Need to consider relative motion of both beams in t and z: 2 c y ( t , z ) 0 ( y1 y2 ) 1 z t 2 2 c y ( t , z ) 0 ( y1 y2 ) 2 z t 2 Classic coupled EoM. 2 2 Dy c 2 6 sz 2 0 Kink Instability Assuming solutions of the form y1(2) a1(2) exp i kz t and substituting into EoM leads to the dispersion relation: 2 c 2 k 2 02 4 02 c 2 k 2 04 Motion becomes unstable when 2 0, which occurs when k 2 0 c Kink Instability Exponential growth rate: 4 2 c 2 k 2 4 2 c 2 k 2 0 0 0 Maximum growth rate when Remember! 1 2 3 0 ; i 0 2 c 2 k 3 sz 3 sz t 2 c 2 c t 3s z / c Thus ‘amplification’ factor of an initial offset is: 1 0 t exp exp 2 2 2 1 4 0.6 Dy e For our previous example with Dy ~28, factor ~ 3 Dy Kink Instability y 0.1s y Dy 20 s z 300 μm Pinch Enhancement L Lgeom H H= enhancement factor results of simulations: 2y exp 2 4s y High Dy example: TESLA 500 Dy 24 Disruption Angle Dy Remembering definition of Dy sz f The angles after collision are characterised by 0 Dxs x sz Dys y sz 2 Nre 2 Nre (s x s y ) s x Numbers from our previous example give 0 467 μrad OK for horizontal plane where Dx<1 For vertical plane (strong focusing Dy > 1), particles oscillate: previous linear approximation: y( z ) Dy 3s 2 z y( z ); 3 z sy 2 Dy 3 sz 1 4 sy 0 1 1 3 Dy 4 67 μrad 2 Disruption Angle: simulation results 250 1000 200 800 150 600 100 400 50 200 0 0 - 400 - 200 0 200 400 horizontal angle (mrad) - 400 - 200 0 200 vertical angle (mrad) Important in designing IR (spent-beam extraction) 400 Beam-Beam Animation Wonderland Animations produced by A. Seryi using the GUINEAPIG beam-beam simulation code (written by D. Schulte, CERN). Examples of GUINEAPIG Simulations NLC parameters Dy~12 Nx2 Dy~24 Examples of GUINEAPIG Simulations NLC parameters Dy~12 Luminosity enhancement HD ~ 1.4 Not much of an instability Examples of GUINEAPIG Simulations Nx2 Dy~24 Beam-beam instability is clearly pronounced Luminosity enhancement is compromised by higher sensitivity to initial offsets Beam-beam deflection Sub nm offsets at IP cause large well detectable offsets (micron scale) of the beam a few meters downstream Beam-beam deflection allow to control collisions Examples of GUINEAPIG Simulations Examples of GUINEAPIG Simulations Beam-Beam Kick Beam-beam offset gives rise to an equal and opposite mean kick to the bunches – important signal for feedback! For small disruption ( D1) and offset (y/sy<<1) 1 y bb 0 2 sy For large disruption or offset, we introduce the form factor F: 1 bb 0 F y / s y 2 F () Long Range Kink Instability & Crossing Angle To avoid parasitic bunch interactions in the IR, a horizontal crossing angle is introduced: ctb c X 2 angle fc ctb l 2 parasitic beam-beam kick: r 2 Nre r r s x, y Long Range Kink Instability & Crossing Angle y IP ip e+ 1 0 F ( ) 2 small vertical offset e ( = y/s ) gives y rise to beam-beam kick y l l 2 Nre ip 2 X Nre 0 F ( ) lfc2 resulting vertical offset at parasitic crossing gives next incoming bunches additional vertical kick: IP offset increases instability Long Range Kink Instability & Crossing Angle offset at IP of k-th bunch: k k k (k l )tb c distance from IP to encounter with l-th bunch (l < k) llk 2 contribution from encounter with l-th bunch: k k ,0 llk,lk / s y k ,0 Nre 0 f sy 2 c F ( l ) k k k k ,0 fc2s y F ( l ) NB. independent of llk s x / s z k k ,0 C F ( i ); C 2 Dx Dy f s f i 1 c y c k 1 total offset: 2 Nre 0 2 Nre 0 2 Long Range Kink Instability & Crossing Angle Assuming all bunches have same initial offset: k ,0 0 For small disruption and small offsets, F (i ) i k (1 C )k 1 0 s x / s z since C Dx Dy f c thus (mb 1)C 1 example: Dx,y = 0.1, 10 sx = 220 nm sz = 100 mm fc = 20 mrad 2 1 k 1 (k 1)C 0 where mb = number of interacting bunches C = 0.012 mb < 80 for factor of 2 increase Crab Crossing x s x , projected s x2 fc2s z2 fcs z 20mr 100μm 2μm factor 10 reduction in L! use transverse (crab) RF cavity to ‘tilt’ the bunch at IP x RF kick ˆ z 2 V 2 z RF V ( z ) VˆRF sin VˆRF fc 4 b cav b ip sz RF Beamstrahlung Magnetic field of bunch B = E/c 2 Emax qN Bmax 1160Tesla Peak field: c 2 0 cs xs z From classical theory, power radiated is given by cC E 4 5 -3 P ; C 8.85 10 m ..GeV 2 r 2 For E = 250 GeV and sz = 300mm: 1 Erad P t P r sz c cB 1.4 m-1 E 32 GeV E/E ~ 12% note: s z / r 200μrad 1/ 2μrad Beamstrahlung Most important parameter is 2 c e 2 2B e 2 3 E r Bs m0 c e r critical photon frequency B Bs beam magnetic field Fm em field tensor p electron 4-momentum F m Compton wavelength local bending radius Schwinger’s critical field (= 4.4 GTesla) 2 p Beamstrahlung: photon spectrum NOT classical synchrotron radiation spectrum! Need to use Sokolov-Ternov formula: 10 FBS y2 K 5 3 ( )d K 2 3 ( ) 1 y 5 10 1 1 0.5 classical y quantum theoretical E 2 y 1 3 1 y c 1 y 1/ 3 0.1 0.05 0.01 0.001 0.1 0.005 0.01 0.05 0.1 y /E 0.5 1 Beamstrahlung Numbers average and maximum avr 5 Nre e 6 s z (s x s y ) max 2.4 avr photons per electron: average energy loss: BS s z avr n 2.54 2/3 1 e avr s z 2avr E 1.24 2/3 2 E e 1 (1.5 avr ) BS and n (and hence ) talk directly to luminosity spectrum and backgrounds Beamstrahlung energy loss In lecture 1, we used the following equation to derive our luminosity scaling law BS ere3 Ecm N2 0.86 2m0c2 s z (s x s y )2 Now we have this: BS with s z 2avr 1.24 2/3 2 e 1 (1.5 avr ) avr 5 Nre e 6 s z (s x s y ) under what regime is our original expression valid? Luminosity scaling revisited b y* s z BS y ,n low beamstrahlung regime 1: L Pbeam high beamstrahlung regime 1: BS L Pbeam s z y ,n 3 homework: derive high BS scaling law 2 Beamstrahlung Numbers: example E 500GeV s x 220 nm avr 0.28 s y 2 nm n 1.3 s x 110μm BS 7.5% max 0.66 N 0.75 1010 TESLA E ,c 210 GeV Why Beamstrahlung is bad • Large number of high-energy photons interact with electron (positron) beam and generate e+e pairs – Low energies (0.6), pairs made by incoherent process (photons interact directly with individual beam particles) – High energies (0.6100), coherent pairs are generated by interaction of photons with macroscopic field of bunch. – Very high energies (U100), coherent direct trident production e e e+ e TESLA NLC CLIC 0.5TeV ~ 0.06 1TeV ~ 0.28 3TeV ~ 9 • Beamstrahlung degrades Luminosity Spectrum Pair Production • Incoherent e+e pairs 0.6 – Breit-Wheeler: – Bethe-Heitler: – Landau-Lifshitz: e e e e e e e e e e e e • Coherent e+e pairs 0.6100 – threshold defined by 10 5 10 1 1 0.5 for >1 1/ 3 0.1 0.05 0.01 0.001 0.1 0.005 0.01 0.05 0.1 y /E 0.5 1 2B m0 c 2 Bs E 1 / E ~ O(1) 1 for intermediate colliders (Ecm<1TeV), incoherent pairs dominate Pair Production e+e pairs are a potential major source of background PT (GeV/c) Most important: angle with beam axis () and transverse momentum PT. 1 0.1 0.01 0.1 l d rd d vertex detector (rad) 1 pairs curl-up (spiral) in PT solenoid field of r rd cBz detector Summary • Single pass collider allows us to use very strong beam-beam to increase luminosity • beam-beam is characterised by following important parameters: – Dy = sz/f – – BS [=f(av)] defines pinch effect (HD), kink instability, dynamics QM effects, backgrounds, energy loss, lumi spectrum • strong-strong regime requires simulation (e.g. GUINEAPIG). Analytical treatments limited.