* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Modern Physics
Monte Carlo methods for electron transport wikipedia , lookup
ALICE experiment wikipedia , lookup
Dirac equation wikipedia , lookup
Identical particles wikipedia , lookup
Compact Muon Solenoid wikipedia , lookup
ATLAS experiment wikipedia , lookup
Grand Unified Theory wikipedia , lookup
Nuclear structure wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
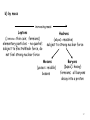
Standard Model wikipedia , lookup
Relativistic quantum mechanics wikipedia , lookup
Electron scattering wikipedia , lookup
Nuclear force wikipedia , lookup
Modern Physics Unit 14: Relativistic Kinematics Lecture 14.2: Advanced Topics Ron Reifenberger Professor of Physics Purdue University 1 What Next? – Topic I: Relativistic Schrodinger Equation In free-space: E=p2/2m → E ↔ i ∂ ∂t p ↔ −i ∇ ∂ 2 2 Schrodinger (1926 ) : i Ψ = − ∇ Ψ (non − relativistic) ∂t 2m In free space: E2=p2c2+m2c4 → E2-p2c2-m2c4=0 E −c 2 3 2 2 2 4 0 p − m c = ∑ i i =1 2 ∂ Klein − Gordon (1926 ) : − 2 2 Ψ + 2 c 2 ∇ 2 Ψ − m 2 c 4 Ψ =0 ∂t Klein-Gordon describes a free, relativistic spinless particle. It requires two initial conditions [Ψ(t=0) and ∂Ψ/∂t(t=0)] because of 2nd derivative wrt time. Therefore specifying a wavefunction Ψ at t=0 is insufficient to uniquely specify the system’s behavior. 2 Dirac’s Relativistic Wave Equation Dirac (1928) : E = ( mc ) 3 2 2 i o =i 1 =i 1 2 2 +c 3 2 ∑p α mc + c ∑ α i pi = ∂ imc 2 Ψ + cα ∇Ψ + α o Ψ =0 ∂t = α α1 x + α 2 y + α 3 z not true for numbers, OK for matrices ! four 1st order differential equations ψ 1 (r , t ) ψ (r, t ) Ψ = 2 Spinors ψ 3 (r , t ) ψ ( r 4 , t ) Predicts spin and anti-particles! 3 The non-relativistic limit for H atom Dirac’s Relativistic Wave Equation in the non-relativistic limit takes the form Relativistic correction to KE Spin-orbit coupling Energy correction if electron and proton are at same location 4 What Next? – Topic II: Forces in Nature Fundamental Forces • • Gravitational Electromagnetic ElectroWeak Strong (nuclear) E Traditional Field view: the field generated by object No. 1 acts on object No. 2 E= Q r 2 4πε o r F = q2 E 1 Q - q 2 5 Virtual particles Object No. 1 emits a virtual (short-lived) exchange particle which transfers momentum to object No. 2. (F=dp/dt) Image from http://hepwww.rl.ac.uk/public/bigbang/file5.html For every Force there is a Force carrier Gravitational – graviton? Electromagnetic – photon ElectroWeak Force Weak – charged and neutral vector bosons (spin=1); Particles that decay by the Weak Interaction have lifetimes from 10-12 s to 10-16 s. Strong (between nucleons, between quarks) – pion (meson), gluons Particles that decay by the Strong Interaction have lifetimes from 10-16 s to 10-23 s. Lifetime of elementary particle measures imbalance of forces But…….. we’re getting ahead of the historical story 6 We Already Know about the Electronic Structure of Atoms Periodic Table – Mendeleev 1869 Elements organized by atomic number: ℓ=0 atomic number = Z Organized by atomic number AND chemical activity: ℓ=1 ℓ=2 How do we learn about the internal (nuclear) structure of an atom? 7 Atomic Size Scattering Experiments: The Basic Idea What’s inside the box? B A Two Limiting Scenarios: • Result A: Box is filled with soft, fluffy material • Result B: Box is filled with hard, rigid material 8 Evidence for a Massive Nucleus: Rutherford’s Scattering Experiments (1911) KEY QUESTION: We know gold foil is made of gold atoms that are electrically neutral. But how are the + and charges distributed? (+) Number of Events A few of the particles are backscattered! Typical Rutherford Scattering (172,000 events) x10 4,000 3,000 2,000 1,000 0 0 45 90 135 180 Scattering angle Conservation of energy and momentum imply the presence of small “heavy objects”. Rutherford concludes that the “heavy objects” are roughly ~10,000 times smaller than an atom!! 9 What we knew circa 1935 composition and approximate dimensions Atom (diameter ≅ 0.2 nm) Nucleus (diameter≅3 fm) electrons neutron proton 1 fm = 1×10-15 m class name hadrons heavy composite particles symbol neutron (1931) n charge 0 (zero) mass spin 1.675 x 10-27 kg 1/2 proton (1919) leptons light elementary particle electron (1897) e- P +1.602 x 10-19 C -1.602 x 10-19 C 1.673 x 10-27 kg 1/2 9.109 x 10-31 kg 1/2 10 Classification of Sub-Atomic Particles a) Historical – time of discovery Positron, an anti-electron 11 b) by mass increasing mass Leptons (λϵπτον = thin coin; fermions) elementary particles - no quarks!; subject to ElectroWeak force, do not feel strong nuclear force Hadrons (αδροζ = massive) subject to strong nuclear force Mesons (μεσοσ = middle) bosons Baryons (βαρυζ= heavy) fermions; all baryons decay into a proton 12 Topics we will cover in the next few weeks How to describe nuclear matter: Mass Density, Charge Density How are nuclei held together: Isotopes, Binding Energy How stable are nuclei: Binding Energy vs. Size Nuclear Force and Nuclear Shell model How do unstable nuclei disintegrate: Radioactivity, half-life Can we predict how a nucleus will disintegrate : Q-factor Predict whether a certain nuclear reaction will occur: Q-factor Energetics of low energy nuclear reaction: Q-factor Nuclear Energy: Fission/Fusion reactions 13 Up Next - Nuclear Characteristics 14