Download Integral

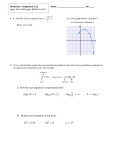
Integral
Integration is an important concept in mathematics, specifically in the field of calculus and,
more broadly, mathematical analysis. Given a function ƒ of a real variable x and an interval
[a, b] of the real line, the integral
is defined informally to be the net signed area of the region in the xy-plane bounded by the
graph of ƒ, the x-axis, and the vertical lines x = a and x = b.
The term "integral" may also refer to the notion of antiderivative, a function F whose
derivative is the given function ƒ. In this case it is called an indefinite integral, while the
integrals discussed in this article are termed definite integrals. Some authors maintain a
distinction between antiderivatives and indefinite integrals.
The principles of integration were formulated independently by Isaac Newton and Gottfried
Leibniz in the late seventeenth century. Through the fundamental theorem of calculus, which
they independently developed, integration is connected with differentiation: if ƒ is a
continuous real-valued function defined on a closed interval [a, b], then, once an
antiderivative F of ƒ is known, the definite integral of ƒ over that interval is given by
For example, consider the curve y = f(x) between x = 0 and x = 1, with f(x) = √x. We ask:
What is the area under the function f, in the interval from 0 to 1?
and call this (yet unknown) area the integral of f. The notation for this integral will be
As a first approximation, look at the unit square given by the
sides x = 0 to x = 1 and y = f(0) = 0 and y = f(1) = 1. Its
area is exactly 1. As it is, the true value of the integral must
be somewhat less. Decreasing the width of the approximation
rectangles shall give a better result; so cross the interval in
five steps, using the approximation points 0, 1⁄5, 2⁄5, and so
on to 1. Fit a box for each step using the right end height of
each curve piece, thus √1⁄5, √2⁄5, and so on to √1 = 1.
Summing the areas of these rectangles, we get a better
approximation for the sought integral, namely
Notice that we are taking a sum of finitely many function values of f, multiplied with the
differences of two subsequent approximation points. We can easily see that the
approximation is still too large. Using more steps produces a closer approximation, but will
never be exact: replacing the 5 subintervals by twelve as depicted, we will get an
approximate value for the area of 0.6203, which is too small. The key idea is the transition
from adding finitely many differences of approximation points multiplied by their respective
function values to using infinitely fine, or infinitesimal steps.
As for the actual calculation of integrals, the fundamental theorem of calculus, due to Newton
and Leibniz, is the fundamental link between the operations of differentiating and integrating.
Applied to the square root curve, f(x) = x1/2, it says to look at the antiderivative F(x) = 2⁄3x3/2,
and simply take F(1) − F(0), where 0 and 1 are the boundaries of the interval [0,1]. (This is
a case of a general rule, that for f(x) = xq, with q ≠ −1, the related function, the so-called
antiderivative is F(x) = (xq+1)/(q + 1).) So the exact value of the area under the curve is
computed formally as
There are many useful integral equations, belows are basic integral equation for ECON206
class.
1)
x dx
2)
kx dx
3) if b
x
k
b
x dx
a, c , then
k
f x dx
x
f x dx
a
k
b
a
f x dx
Exponential Function
The exponential function ex can be defined, in a variety of equivalent ways, as an infinite
series. In particular it may be defined by a power series:
.
It is also the following limit:
And e1 = e = 2.71828…
The basic property of exponential function is
And the most important property of exponential function is
This implies that
e dx
e
Logarithm
The logarithm of x to the base b is written logb(x) or, if the base is implicit, as log(x). So, for
a number x, a base b and an exponent y,
An important feature of logarithms is that they reduce multiplication to addition, by the
formula:
If b=e(exponential), let log a
ln a and we call it natural log.
Since exponential and logarithmic functions of the same base are inverses of one another, if
you compose the two functions together, they will cancel one another out.
Since you will see common and natural logs most often, here is that inverse relationship
expressed in terms of their respective bases:
Formally, ln(a) may be defined as the area under the graph of 1/x from 1 to a, that is as the
integral,
This defines a logarithm because it satisfies the
fundamental property of a logarithm:
This can be demonstrated by letting
as follows:
The number e can then be defined as the unique real number a such that ln(a) = 1.
Since logarithmic and exponential functions are one another's inverses, it is easy to construct
the graph of any logarithmic function y = log a x based on the corresponding graph of y = a x .
Graphs of inverse functions are reflections of one another across the line y = x, since each
graph contains the coordinates of the other graph, with each coordinate pair reversed. It is
no surprise, then, that because all exponential graphs of the form y = a x contain the point
(0,1), then all logarithmic graphs of the form y = log a x contain the point (1,0).
In Figure 1 , you can visually verify that the graphs of the natural logarithmic and natural
exponential functions are, indeed, reflections of one another about the line y = x.
Figure 1 The graphs of y = e x and y = in x are reflections of one another about the line y = x, as are all inverse
functions.
Note that the domain of ln x, like all logarithmic functions of form y = log a x, is (0,∞).
Although it might appear that the y values of the logarithmic graph “level out,” as if
approaching a horizontal asymptote, they do not. In fact, a logarithmic graph will grow
infinitely tall, albeit much, much slower than its sister the exponential function. A range of
(−∞,∞) for the logarithmic functions makes sense, since their inverses are exponential
functions and have domains of (−∞,∞).
As we can find that ln2<1 and ln4>1 by Figure 1
and recall that e1 =a Ù ln a=1
so, 2<e<4 (actually e=2.71828…)