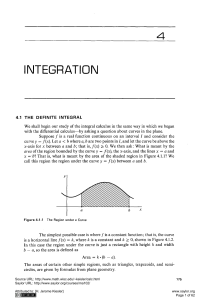
2 HYPERBOLIC FUNCTIONS
... By implication when using Osborn's rule, where the function tanh x occurs, it must be regarded as involving sinh x. Therefore, to convert the formula sec2 x = 1 + tan2 x ...
... By implication when using Osborn's rule, where the function tanh x occurs, it must be regarded as involving sinh x. Therefore, to convert the formula sec2 x = 1 + tan2 x ...
Week 7: Limits at Infinity. - MA161/MA1161: Semester
... and say that the limit of f(x) as x approaches +∞ (or −∞) is L, if we can make f(x) as close to L as we would like, by simply choosing x as a sufficiently large positive (or negative) number. This may also be written as f(x) → L as x → ∞ (or x → −∞). In either case, the line y = L is called a horizo ...
... and say that the limit of f(x) as x approaches +∞ (or −∞) is L, if we can make f(x) as close to L as we would like, by simply choosing x as a sufficiently large positive (or negative) number. This may also be written as f(x) → L as x → ∞ (or x → −∞). In either case, the line y = L is called a horizo ...
On the Classification of Topological Field Theories
... A 7→ tr(A). Consequently, Z(S ) is given by the trace of the identity map from V to itself: in other words, the dimension of V . Remark 1.1.10. Example 1.1.9 illustrates some central themes which will reappear (in a more sophisticated form) later in this paper. A priori, the specification of a topol ...
... A 7→ tr(A). Consequently, Z(S ) is given by the trace of the identity map from V to itself: in other words, the dimension of V . Remark 1.1.10. Example 1.1.9 illustrates some central themes which will reappear (in a more sophisticated form) later in this paper. A priori, the specification of a topol ...
On Undefined and Meaningless in Lambda Definability
... on one hand they led Church to his Church Thesis and on the other hand they demonstrate that lambda calculus is a paradigmatic programming language [3]. The first definition of lambda definability dealt with total functions, as partial recursive functions had not yet been defined. I Definition 1. A ...
... on one hand they led Church to his Church Thesis and on the other hand they demonstrate that lambda calculus is a paradigmatic programming language [3]. The first definition of lambda definability dealt with total functions, as partial recursive functions had not yet been defined. I Definition 1. A ...
Infinite Sequences
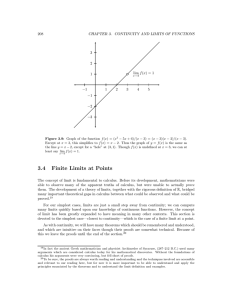
... when n ! 1. It should also be noted that if lim an = L, then lim an+1 = L. n!1 n!1 In fact, lim an+p = L for any positive integer p. Graphically, the meaning of lim an = L is as follows. Consider the sequence shown on …gure 5 whose plot is represented by the dots. The sequence appears to have 3 as i ...
... when n ! 1. It should also be noted that if lim an = L, then lim an+1 = L. n!1 n!1 In fact, lim an+p = L for any positive integer p. Graphically, the meaning of lim an = L is as follows. Consider the sequence shown on …gure 5 whose plot is represented by the dots. The sequence appears to have 3 as i ...
Conjugation spaces 1 Introduction
... countably many successive adjunction of collections of conjugation cells. A conjugation cell (of dimension 2k ) is a space with involution which is equivariantly homeomorphic to the closed disk of radius 1 in R2k , equipped with a linear involution with exactly k eigenvalues equal to −1. At each ste ...
... countably many successive adjunction of collections of conjugation cells. A conjugation cell (of dimension 2k ) is a space with involution which is equivariantly homeomorphic to the closed disk of radius 1 in R2k , equipped with a linear involution with exactly k eigenvalues equal to −1. At each ste ...
Mean Square Calculus for Random Processes
... (such as means and variances) are of interest, not individual sample functions. Many applications are served well by a calculus based on mean-square convergence concepts similar to those introduced in Chapter 11. Such a mean-square calculus discards the difficulties of having to deal with all sample ...
... (such as means and variances) are of interest, not individual sample functions. Many applications are served well by a calculus based on mean-square convergence concepts similar to those introduced in Chapter 11. Such a mean-square calculus discards the difficulties of having to deal with all sample ...
There are three most common inverse trigonometric functions
... The inverse cosine function is written as y = cos−1 (x) or y = arccos x. (Not to be confused with y = 1/ cos x.) The domain of arccos x is the interval [−1, 1] and its range is [0, π]. For any number x between −1 and 1, arccos x is the angle between 0 and π whose cosine is x. In other words, let −1 ...
... The inverse cosine function is written as y = cos−1 (x) or y = arccos x. (Not to be confused with y = 1/ cos x.) The domain of arccos x is the interval [−1, 1] and its range is [0, π]. For any number x between −1 and 1, arccos x is the angle between 0 and π whose cosine is x. In other words, let −1 ...
Course Title:
... foundation of mathematics is the idea of a function. Functions express the way one variable quantity is related to another quantity. Calculus was invented to deal with the rate at which a quantity varies, particularly if that rate does not stay constant. Clearly, this course needs to begin with a th ...
... foundation of mathematics is the idea of a function. Functions express the way one variable quantity is related to another quantity. Calculus was invented to deal with the rate at which a quantity varies, particularly if that rate does not stay constant. Clearly, this course needs to begin with a th ...
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces. They are sometimes called Lebesgue spaces, named after Henri Lebesgue (Dunford & Schwartz 1958, III.3), although according to the Bourbaki group (Bourbaki 1987) they were first introduced by Frigyes Riesz (Riesz 1910).Lp spaces form an important class of Banach spaces in functional analysis, and of topological vector spaces.Lebesgue spaces have applications in physics, statistics, finance, engineering, and other disciplines.