10.3
... graph of y = f (x) if f (x) or f (x) - as x a+ or x a–. That is, f (x) either increases or decreases without bound as x approaches a from the right or from the left. Note: If any one of the four possibilities is satisfied, this makes x = a a vertical asymptote. Most of the time, the limit ...
... graph of y = f (x) if f (x) or f (x) - as x a+ or x a–. That is, f (x) either increases or decreases without bound as x approaches a from the right or from the left. Note: If any one of the four possibilities is satisfied, this makes x = a a vertical asymptote. Most of the time, the limit ...
Transcript - MIT OpenCourseWare
... All right. That's part a. Let's go on to part b. So, you know, you've probably noticed that these questions are all fairly similar. The only real complication is that I've been increasing the number of variables. But of course, you know how to take a gradient for a function of three variables as wel ...
... All right. That's part a. Let's go on to part b. So, you know, you've probably noticed that these questions are all fairly similar. The only real complication is that I've been increasing the number of variables. But of course, you know how to take a gradient for a function of three variables as wel ...
Chapter 1 I. Fibre Bundles
... By condition (2), the fibre of a principal G-bundle is always G. However we generalize to bundles whose fibre is some other G-space as follows. Let G be a topological group. Let p : E → B be a principal G-bundle and let F be a G-space on which the action of G is effective. The fibre bundle with stru ...
... By condition (2), the fibre of a principal G-bundle is always G. However we generalize to bundles whose fibre is some other G-space as follows. Let G be a topological group. Let p : E → B be a principal G-bundle and let F be a G-space on which the action of G is effective. The fibre bundle with stru ...
real-analysis-richard-bass-3rd-edition
... are covered in Chapters 11–15. Many courses in real analysis stop at this point. Others also include some or all of the following topics: the Fourier transform, the Riesz representation theorem, Banach spaces, and Hilbert spaces. We present these in Chapters 16–19. Topology and probability are cours ...
... are covered in Chapters 11–15. Many courses in real analysis stop at this point. Others also include some or all of the following topics: the Fourier transform, the Riesz representation theorem, Banach spaces, and Hilbert spaces. We present these in Chapters 16–19. Topology and probability are cours ...
Differentiable manifolds
... In Geometry 1 we have dealt with parametrized curves and surfaces in R or R3 . The definitions we have seen for the two notions are analogous to each other, and we shall begin by generalizing them to arbitrary dimensions. As a result we obtain the notion of a parametrized m-dimensional manifold in R ...
... In Geometry 1 we have dealt with parametrized curves and surfaces in R or R3 . The definitions we have seen for the two notions are analogous to each other, and we shall begin by generalizing them to arbitrary dimensions. As a result we obtain the notion of a parametrized m-dimensional manifold in R ...
Real analysis for graduate students
... are covered in Chapters 11–15. Many courses in real analysis stop at this point. Others also include some or all of the following topics: the Fourier transform, the Riesz representation theorem, Banach spaces, and Hilbert spaces. We present these in Chapters 16–19. Topology and probability are cours ...
... are covered in Chapters 11–15. Many courses in real analysis stop at this point. Others also include some or all of the following topics: the Fourier transform, the Riesz representation theorem, Banach spaces, and Hilbert spaces. We present these in Chapters 16–19. Topology and probability are cours ...
Random Involutions and the Distinct Prime Divisor Function
... Given a natural number n and a pair (a, b) of non-negative integers such that 2a + b = n, the probability that an involution on Fn2 is isomorphic to the involution corresponding to F2 [Z/2]a x Fb2 is: 1/| Aut(a, b)| ...
... Given a natural number n and a pair (a, b) of non-negative integers such that 2a + b = n, the probability that an involution on Fn2 is isomorphic to the involution corresponding to F2 [Z/2]a x Fb2 is: 1/| Aut(a, b)| ...
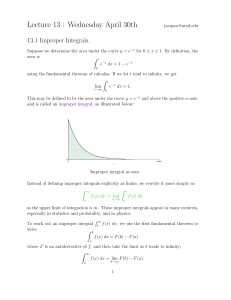
Lecture 13 : Wednesday April 30th
... 12.3 Other improper integrals In all the integrals so far, the functions we have dealt with are continuous on the range of integration. Another type of improper integral arises when the integrand is discontinuous over the range of integration, due to the presence of vertical asymptotes. For example, ...
... 12.3 Other improper integrals In all the integrals so far, the functions we have dealt with are continuous on the range of integration. Another type of improper integral arises when the integrand is discontinuous over the range of integration, due to the presence of vertical asymptotes. For example, ...
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces. They are sometimes called Lebesgue spaces, named after Henri Lebesgue (Dunford & Schwartz 1958, III.3), although according to the Bourbaki group (Bourbaki 1987) they were first introduced by Frigyes Riesz (Riesz 1910).Lp spaces form an important class of Banach spaces in functional analysis, and of topological vector spaces.Lebesgue spaces have applications in physics, statistics, finance, engineering, and other disciplines.