A Partial Characterization of Ehrenfeucht-Fra¨ıss´e Games on Fields and Vector Spaces
... spaces of the same dimension over the same field are isomorphic. We let I j be the set of all partial isomorphisms from a j-dimensional subspace of Fn to a j-dimensional subspace of Fm : I j = {f : Sn ⊆ Fn → Sm ⊆ Fm , dim(Sn /F) = dim(Sm /F) = j} Then we consider the partial isomorphisms generated as ...
... spaces of the same dimension over the same field are isomorphic. We let I j be the set of all partial isomorphisms from a j-dimensional subspace of Fn to a j-dimensional subspace of Fm : I j = {f : Sn ⊆ Fn → Sm ⊆ Fm , dim(Sn /F) = dim(Sm /F) = j} Then we consider the partial isomorphisms generated as ...
A Basis Theory Primer
... spaces. In Chapter 2, we define what it means for a series to converge, and study several more restrictive forms of convergence, including unconditional convergence in particular. Chapter 3 presents some additional results on unconditional convergence that apply to the specific case of Hilbert space ...
... spaces. In Chapter 2, we define what it means for a series to converge, and study several more restrictive forms of convergence, including unconditional convergence in particular. Chapter 3 presents some additional results on unconditional convergence that apply to the specific case of Hilbert space ...
The Magnitude of Metric Spaces
... Many mathematical objects carry a canonical notion of size. Sets have cardinality, vector spaces have dimension, topological spaces have Euler characteristic, and probability spaces have entropy. This work adds a new item to the list: metric spaces have magnitude. Already, several cardinality-like i ...
... Many mathematical objects carry a canonical notion of size. Sets have cardinality, vector spaces have dimension, topological spaces have Euler characteristic, and probability spaces have entropy. This work adds a new item to the list: metric spaces have magnitude. Already, several cardinality-like i ...
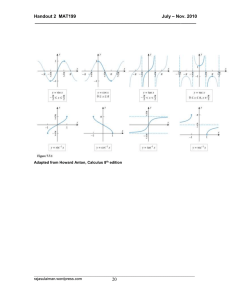
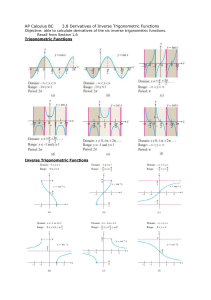
Trig Course Outline - Northwest Arkansas Community College
... Review of Exponential and Logarithmic Functions, Their Graphs, Their Properties, and Their Applications ...
... Review of Exponential and Logarithmic Functions, Their Graphs, Their Properties, and Their Applications ...
Week #2:
... Separation of process and measure Measure(2) equivalent to measure (1) if measure (2) associates positive probability to all events (1) that have positive probability under measure (1). Risk neutral probabilities equivalent martingale measure Under the risk neutral measure the expected return of a ...
... Separation of process and measure Measure(2) equivalent to measure (1) if measure (2) associates positive probability to all events (1) that have positive probability under measure (1). Risk neutral probabilities equivalent martingale measure Under the risk neutral measure the expected return of a ...
Unbounded absolute weak convergence in Banach lattices
... Remark 17. Note that when E is order continuous, by Theorem 13, uaw-convergence and un-convergence are the same. Thus, we can restate Proposition 15 and Proposition 16 in term of un-convergence, too. In this case, Proposition 16 can be obtained using Theorem 13 and [KMT, Corollary 4.6] with a differe ...
... Remark 17. Note that when E is order continuous, by Theorem 13, uaw-convergence and un-convergence are the same. Thus, we can restate Proposition 15 and Proposition 16 in term of un-convergence, too. In this case, Proposition 16 can be obtained using Theorem 13 and [KMT, Corollary 4.6] with a differe ...
Continuity of Local Time: An applied perspective
... This point could hardly have been more aptly made with regard to the perspective of the present paper. The focus of this paper is on identifying the way in which continuity/discontinuity properties of certain local times of a diffusive Markov process inform interfacial discontinuities in large scale ...
... This point could hardly have been more aptly made with regard to the perspective of the present paper. The focus of this paper is on identifying the way in which continuity/discontinuity properties of certain local times of a diffusive Markov process inform interfacial discontinuities in large scale ...
Example sheet 1
... Exercise 2.9 (Bayes’ urn). A random number Θ is chosen uniformly between 0 and 1, and a coin with probability Θ of heads is minted. The coin is tossed repeatedly. Let Bn be the number of heads in n tosses. Prove that (Bn ) has exactly the same probabilistic structure as the (Bn ) sequence in Exercis ...
... Exercise 2.9 (Bayes’ urn). A random number Θ is chosen uniformly between 0 and 1, and a coin with probability Θ of heads is minted. The coin is tossed repeatedly. Let Bn be the number of heads in n tosses. Prove that (Bn ) has exactly the same probabilistic structure as the (Bn ) sequence in Exercis ...
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces. They are sometimes called Lebesgue spaces, named after Henri Lebesgue (Dunford & Schwartz 1958, III.3), although according to the Bourbaki group (Bourbaki 1987) they were first introduced by Frigyes Riesz (Riesz 1910).Lp spaces form an important class of Banach spaces in functional analysis, and of topological vector spaces.Lebesgue spaces have applications in physics, statistics, finance, engineering, and other disciplines.