Factorization of Period integrals
... main result is that if this linear form is non-zero, then it can be written as a tensor product of local linear forms. This is a rather startling result, since there is no local property of uniqueness which guarantees in advance the existence of such a decomposition. In more detail, if 6 is distingu ...
... main result is that if this linear form is non-zero, then it can be written as a tensor product of local linear forms. This is a rather startling result, since there is no local property of uniqueness which guarantees in advance the existence of such a decomposition. In more detail, if 6 is distingu ...
Functional analysis - locally convex spaces
... d) S separates E i.e. if x is a non-zero element of E, then there is a p ∈ S with p(x) 6= 0. If S is a family of seminorms which satisfies only d), then there is a smallest irreducible family of seminorms which contains S. It is called the irreducible hull of S and denoted by S̃. (S̃ is the interse ...
... d) S separates E i.e. if x is a non-zero element of E, then there is a p ∈ S with p(x) 6= 0. If S is a family of seminorms which satisfies only d), then there is a smallest irreducible family of seminorms which contains S. It is called the irreducible hull of S and denoted by S̃. (S̃ is the interse ...
VECTOR SUPERIOR AND INFERIOR Y. Chiang In this paper, all
... The notion of topological pseudomonotonicity has been generalized in [3] to bifunctions f of K × K into an ordered topological vector space. In a very recent paper, Chadli, Schaible and Yao established an existence result for regularized equilibrium problems with the corresponding real functions top ...
... The notion of topological pseudomonotonicity has been generalized in [3] to bifunctions f of K × K into an ordered topological vector space. In a very recent paper, Chadli, Schaible and Yao established an existence result for regularized equilibrium problems with the corresponding real functions top ...
1 - OSU Department of Mathematics
... injective but not invertible; the range consists in the of functions vanishing at zero, right-differentiable at zero, a strict subspace of C[0, 1]. Another example is (a1 , a2 , ...) → (0, a1 , a2 , ...). 7. Operators which are not closed (closable more precisely) are ill-behaved in many ways. Note ...
... injective but not invertible; the range consists in the of functions vanishing at zero, right-differentiable at zero, a strict subspace of C[0, 1]. Another example is (a1 , a2 , ...) → (0, a1 , a2 , ...). 7. Operators which are not closed (closable more precisely) are ill-behaved in many ways. Note ...
Notes on Locally Convex Topological Vector Spaces
... space of germs of holomorphic functions at z0 . It is a Hausdorff l.c.s. because there are enough continuous linear functionals to separate points. In fact, for each non-negative integer n, the nth derivative map f → f (n) (z0 ) is a continuous linear functional on H(U ) for each U ∈ Uz0 which is co ...
... space of germs of holomorphic functions at z0 . It is a Hausdorff l.c.s. because there are enough continuous linear functionals to separate points. In fact, for each non-negative integer n, the nth derivative map f → f (n) (z0 ) is a continuous linear functional on H(U ) for each U ∈ Uz0 which is co ...
Lecture 1: Connections on principal fibre bundles
... preserved by the equivalence relation, which uses left multiplication by the transition functions. (Associativity of group multiplication guarantees that right and left multiplications commute.) Example 1.1 (Möbius band). The boundary of the Möbius band is an example of a nontrivial principal Z2 -bu ...
... preserved by the equivalence relation, which uses left multiplication by the transition functions. (Associativity of group multiplication guarantees that right and left multiplications commute.) Example 1.1 (Möbius band). The boundary of the Möbius band is an example of a nontrivial principal Z2 -bu ...
Bornological versus topological analysis in metrizable spaces
... homology. This derived functor agrees with the completion if and only if the space in question is subcomplete, that is, a subspace of a complete space. We obtain some sufficient conditions for subcompleteness. They imply that the spaces that we must complete to compute the local cyclic homology of a ...
... homology. This derived functor agrees with the completion if and only if the space in question is subcomplete, that is, a subspace of a complete space. We obtain some sufficient conditions for subcompleteness. They imply that the spaces that we must complete to compute the local cyclic homology of a ...
Abstract ordered compact convex sets and the algebras of the (sub
... Theorem 4]. His proof carries over to arbitrary closed binary relations: Lemma 2.2. Let X be a topological space with a binary relation the graph G of which is closed. (a) For any compact subset K, the lower set and the upper set ↓K =def {x ∈ X | (x, b) ∈ G for some b ∈ K} ↑K =def {x ∈ X | (b, x) ∈ ...
... Theorem 4]. His proof carries over to arbitrary closed binary relations: Lemma 2.2. Let X be a topological space with a binary relation the graph G of which is closed. (a) For any compact subset K, the lower set and the upper set ↓K =def {x ∈ X | (x, b) ∈ G for some b ∈ K} ↑K =def {x ∈ X | (b, x) ∈ ...
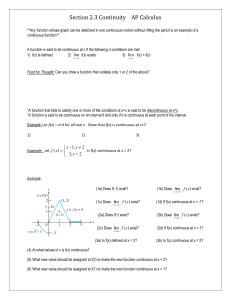
Section 2.3 Continuity AP Calculus - AP Calculus
... there exists at least one value c (a, b) such that f(c) = M. *Corollary: If f(x) is continuous on [a, b] and if f(a) and f(b) are nonzero and have opposite signs, then f(x) has a zero in (a, b). Food for Thought: Consider a plane that takes off and climbs from 0 to 20, 000 feet in twenty minutes. ...
... there exists at least one value c (a, b) such that f(c) = M. *Corollary: If f(x) is continuous on [a, b] and if f(a) and f(b) are nonzero and have opposite signs, then f(x) has a zero in (a, b). Food for Thought: Consider a plane that takes off and climbs from 0 to 20, 000 feet in twenty minutes. ...
convex functions on symmetric spaces, side lengths of polygons and
... system (than ours) consisting of all inequalities where the intersections of Schubert classes is a nonzero multiple of the point class. Thus, our Theorem 1.3 for the complex case is a refinement of their result. In the general real case the polyhedron P3 (p) was determined in [OSj]. However their in ...
... system (than ours) consisting of all inequalities where the intersections of Schubert classes is a nonzero multiple of the point class. Thus, our Theorem 1.3 for the complex case is a refinement of their result. In the general real case the polyhedron P3 (p) was determined in [OSj]. However their in ...
A short proof of the Bolzano-Weierstrass Theorem
... Theorem 1 (Bolzano-Weierstrass Theorem, Version 1). Every bounded sequence of real numbers has a convergent subsequence. To mention but two applications, the theorem can be used to show that if [a, b] is a closed, bounded interval and f : [a, b] → R is continous, then f is bounded. One may also invo ...
... Theorem 1 (Bolzano-Weierstrass Theorem, Version 1). Every bounded sequence of real numbers has a convergent subsequence. To mention but two applications, the theorem can be used to show that if [a, b] is a closed, bounded interval and f : [a, b] → R is continous, then f is bounded. One may also invo ...
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces. They are sometimes called Lebesgue spaces, named after Henri Lebesgue (Dunford & Schwartz 1958, III.3), although according to the Bourbaki group (Bourbaki 1987) they were first introduced by Frigyes Riesz (Riesz 1910).Lp spaces form an important class of Banach spaces in functional analysis, and of topological vector spaces.Lebesgue spaces have applications in physics, statistics, finance, engineering, and other disciplines.