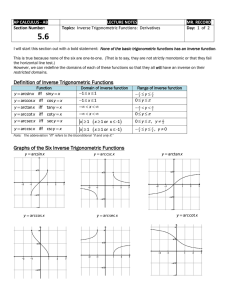
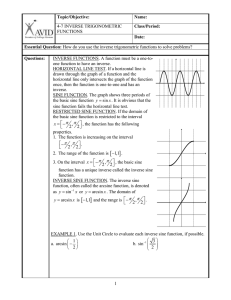
ANTIDERIVATIVES AND AREAS AND THINGS 1. Integration is
... Let’s use this to calculate some areas of familiar objects. The first one I will do and the second one you should try, but please ask if you need help. Example. Using The Area Theorem, calculate the area of a rectangle with base, b, and height h. To use The Area Theorem we need to express this recta ...
... Let’s use this to calculate some areas of familiar objects. The first one I will do and the second one you should try, but please ask if you need help. Example. Using The Area Theorem, calculate the area of a rectangle with base, b, and height h. To use The Area Theorem we need to express this recta ...
The Stong Isoperimetric Inequality of Bonnesen
... polygons that connect finely spaced points running along the curve have lengths that approximate the length L. By removing loops we arrange that the Pn are Jordan polygons that approximate γ in an appropriate manner (in Hausdorff distance). Second rectifiability ensures that γ itself has zero area, ...
... polygons that connect finely spaced points running along the curve have lengths that approximate the length L. By removing loops we arrange that the Pn are Jordan polygons that approximate γ in an appropriate manner (in Hausdorff distance). Second rectifiability ensures that γ itself has zero area, ...
Analytic Functions
... In this chapter, we shall generalize the ideas for polynomials and power series of a complex variable we developed in the previous chapter to general functions of a complex variable. Once we have proved results to determine whether or not a function is analytic, we shall then consider generalization ...
... In this chapter, we shall generalize the ideas for polynomials and power series of a complex variable we developed in the previous chapter to general functions of a complex variable. Once we have proved results to determine whether or not a function is analytic, we shall then consider generalization ...
Note on the convex hull of the Stiefel manifold - FSU Math
... Let p and n be positive integers with p ≤ n. The (compact) Stiefel manifold is the set St(p, n) = {X ∈ Rn×p : X T X = Ip }, where Ip denotes the identity matrix of size p. We view St(p, n) as a subset of Rn×p endowed with the Frobenius norm. The fact that St(p, n) has a natural manifold structure is ...
... Let p and n be positive integers with p ≤ n. The (compact) Stiefel manifold is the set St(p, n) = {X ∈ Rn×p : X T X = Ip }, where Ip denotes the identity matrix of size p. We view St(p, n) as a subset of Rn×p endowed with the Frobenius norm. The fact that St(p, n) has a natural manifold structure is ...
The Meaning of Integration
... in practice, it takes a few years of study to understand the concept of integration. In fact, one grasps the idea of integration only on studying the theory of Riemann3 integration (R-integration) which is the generalization of Cauchy integration to the class of functions which are not necessarily c ...
... in practice, it takes a few years of study to understand the concept of integration. In fact, one grasps the idea of integration only on studying the theory of Riemann3 integration (R-integration) which is the generalization of Cauchy integration to the class of functions which are not necessarily c ...
TRANSFORMS AND MOMENT GENERATING FUNCTIONS There
... and using this together with the power series for the indicator itself we can calculate the moment generating function for any unknown whose pdf is a straight line segment supported on [a, b]. We can also break up the transform process over disjoint intervals. Thus, if f and g are functions with dom ...
... and using this together with the power series for the indicator itself we can calculate the moment generating function for any unknown whose pdf is a straight line segment supported on [a, b]. We can also break up the transform process over disjoint intervals. Thus, if f and g are functions with dom ...
Locally convex topological vector spaces
... Corollary 4.1.10. Every neighborhood of the origin in a t.v.s. is contained in a neighborhood of the origin which is absolutely convex. Note that the converse of Proposition 4.1.9 does not hold in any t.v.s.. Indeed, not every neighborhood of the origin contains another one which is a barrel. This m ...
... Corollary 4.1.10. Every neighborhood of the origin in a t.v.s. is contained in a neighborhood of the origin which is absolutely convex. Note that the converse of Proposition 4.1.9 does not hold in any t.v.s.. Indeed, not every neighborhood of the origin contains another one which is a barrel. This m ...
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces. They are sometimes called Lebesgue spaces, named after Henri Lebesgue (Dunford & Schwartz 1958, III.3), although according to the Bourbaki group (Bourbaki 1987) they were first introduced by Frigyes Riesz (Riesz 1910).Lp spaces form an important class of Banach spaces in functional analysis, and of topological vector spaces.Lebesgue spaces have applications in physics, statistics, finance, engineering, and other disciplines.