2 HYPERBOLIC FUNCTIONS
... Prove the result by converting cosech y and coth y into exponential functions. ...
... Prove the result by converting cosech y and coth y into exponential functions. ...
Section 1.1 Calculus: Areas And Tangents
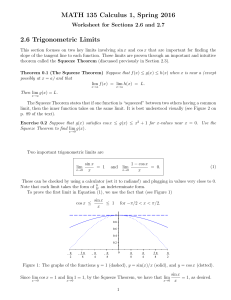
... Example Suppose we wish to find the area inside a circle of radius one centered at the origin. Of course, we have all learned that the answer is π. But why? Indeed, what does it mean to find the area of a disk? Area is best defined for polygons, regions in the plane with line segments for sides. One ...
... Example Suppose we wish to find the area inside a circle of radius one centered at the origin. Of course, we have all learned that the answer is π. But why? Indeed, what does it mean to find the area of a disk? Area is best defined for polygons, regions in the plane with line segments for sides. One ...
B.3 The Beta Function
... The formula of (B.15) is a very useful relation; it establishes the relationship between the Γ(n) function and the factorial n!. We must remember that, whereas the factorial n! is defined only for zero (recall that 0! = 1) and positive integer values, the gamma function exists (is continuous) everyw ...
... The formula of (B.15) is a very useful relation; it establishes the relationship between the Γ(n) function and the factorial n!. We must remember that, whereas the factorial n! is defined only for zero (recall that 0! = 1) and positive integer values, the gamma function exists (is continuous) everyw ...
fx( )= L lim fx( )+ gx( )
... f ( x ) has a limit as x approaches c iff it has left-hand and right-hand limits ...
... f ( x ) has a limit as x approaches c iff it has left-hand and right-hand limits ...
Review sheet Final Exam Math 140 Calculus I
... 4. Recall that the volume of a cylinder is computed as the product of the area of its base by its height. Recall also that the surface area of the wall of a cylinder is given by multiplying the perimeter of the base by the height of the cylinder. A cylindrical container with an open top is being bui ...
... 4. Recall that the volume of a cylinder is computed as the product of the area of its base by its height. Recall also that the surface area of the wall of a cylinder is given by multiplying the perimeter of the base by the height of the cylinder. A cylindrical container with an open top is being bui ...
Understanding Calculus II: Problems, Solutions, and Tips
... understanding of key concepts from physics, including particle motion, velocity, and acceleration. Calculus is often described as the mathematics of change. The concepts of calculus—including velocities, accelerations, tangent lines, slopes, areas, volumes, arc lengths, centroids, curvatures, and wo ...
... understanding of key concepts from physics, including particle motion, velocity, and acceleration. Calculus is often described as the mathematics of change. The concepts of calculus—including velocities, accelerations, tangent lines, slopes, areas, volumes, arc lengths, centroids, curvatures, and wo ...
MAT 123 Practice for Core Competency Exam B With Solutions
... MAT 123 Introduction to Calculus Core Competency Exam B In-lecture Wednesday / Thursday, Week of 3/23-3/27 ...
... MAT 123 Introduction to Calculus Core Competency Exam B In-lecture Wednesday / Thursday, Week of 3/23-3/27 ...
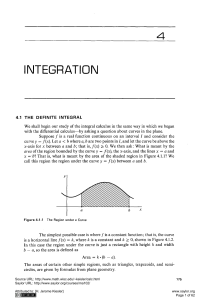
Section 4.1: The Definite Integral
... fj(x)dx. Before plunging into the detailed definition of the integral, we outline the main ideas. First, the region under the curve is divided into infinitely many vertical strips of infinitesimal width dx. Next, each vertical strip is replaced by a vertical rectangle of height f (x ), base dx, and ...
... fj(x)dx. Before plunging into the detailed definition of the integral, we outline the main ideas. First, the region under the curve is divided into infinitely many vertical strips of infinitesimal width dx. Next, each vertical strip is replaced by a vertical rectangle of height f (x ), base dx, and ...
From 135 to 152 Notes on the problem set : 1
... Part 3 The problems in part 3 use L’Hopital’s Rule and applications of eln .. . Since L’Hopital’s Rule requires excellent differentiation skills, make sure that you know how to differentiate very well. Then read up on the topic in Stewart’s book, and try these problems. Since in math 152 your instru ...
... Part 3 The problems in part 3 use L’Hopital’s Rule and applications of eln .. . Since L’Hopital’s Rule requires excellent differentiation skills, make sure that you know how to differentiate very well. Then read up on the topic in Stewart’s book, and try these problems. Since in math 152 your instru ...
Sequences, Series and Taylor Approximation
... The first 12 lectures (Chapters 1-3) contribute to the study blocks MA2730 (for M, FM, MSM and MCS) and MA2712b (for MMS and MCC). Those blocks feed into the assessment blocks MA2812 and MA2815 (for M, FM, MSM and MCS) or MA2810 (for MMS and MCC). The purpose of those lectures is to make you familia ...
... The first 12 lectures (Chapters 1-3) contribute to the study blocks MA2730 (for M, FM, MSM and MCS) and MA2712b (for MMS and MCC). Those blocks feed into the assessment blocks MA2812 and MA2815 (for M, FM, MSM and MCS) or MA2810 (for MMS and MCC). The purpose of those lectures is to make you familia ...
Tutorial on Stochastic Differential Equations
... with initial condition X0 , which could be random. We wish to construct a mathematical model of how the may behave in the presence of noise. We wish for this noise source to be stationary and independent of the current state of the system. We also want for the resulting paths to be continuous. As it ...
... with initial condition X0 , which could be random. We wish to construct a mathematical model of how the may behave in the presence of noise. We wish for this noise source to be stationary and independent of the current state of the system. We also want for the resulting paths to be continuous. As it ...
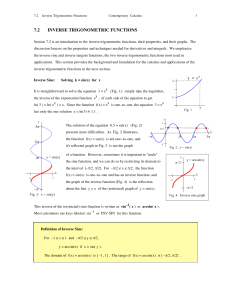
7.2 INVERSE TRIGONOMETRIC FUNCTIONS
... dt tan(θ) = dt ( 4000 ) . Then solve for dt . ) 34. You are observing a rocket launch from a point 3000 feet from the launch pad. You heard on the radio the when the rocket is 5000 feet high its velocity is 100 feet per second. (a) What is the angle of elevation of the rocket when it is 5000 feet up ...
... dt tan(θ) = dt ( 4000 ) . Then solve for dt . ) 34. You are observing a rocket launch from a point 3000 feet from the launch pad. You heard on the radio the when the rocket is 5000 feet high its velocity is 100 feet per second. (a) What is the angle of elevation of the rocket when it is 5000 feet up ...
Pdf - Text of NPTEL IIT Video Lectures
... And we say that since, here the concept of nearness of these y and y tilde has to be made precise, and that is what we do in the following manner? We did we say that this two functions, these two functions y and y tilde are epsilon close, epsilon is the positive quantity, here epsilon close to each ...
... And we say that since, here the concept of nearness of these y and y tilde has to be made precise, and that is what we do in the following manner? We did we say that this two functions, these two functions y and y tilde are epsilon close, epsilon is the positive quantity, here epsilon close to each ...
Introduction to Homogenization and Gamma
... in the variational sense of ;-convergence, which was introduced by E. De Giorgi in the 70s exactly for dealing with problems of this kind. Special relevance will be given to the illustration of the general method, which can be applied, with the due changes, to the study of other types of functionals ...
... in the variational sense of ;-convergence, which was introduced by E. De Giorgi in the 70s exactly for dealing with problems of this kind. Special relevance will be given to the illustration of the general method, which can be applied, with the due changes, to the study of other types of functionals ...
AP Calculus – Final Review Sheet When you see the words …. This
... Typically done with a table of values. Be sure to use only values that are given. If you are given 6 sets of points, you can only do 3 midpoint rectangles. base x0 2 x1 2 x2 ... 2 xn1 xn A ...
... Typically done with a table of values. Be sure to use only values that are given. If you are given 6 sets of points, you can only do 3 midpoint rectangles. base x0 2 x1 2 x2 ... 2 xn1 xn A ...
Week 7: Limits at Infinity. - MA161/MA1161: Semester
... We say that a function f : D → R is continuous, if it is continuous at all points in its domain D. If the domain D consists of intervals, this means that the function needs to be continuous on each interval, in the following sense. A function f : D → R is continuous on an interval I ⊆ D if it is con ...
... We say that a function f : D → R is continuous, if it is continuous at all points in its domain D. If the domain D consists of intervals, this means that the function needs to be continuous on each interval, in the following sense. A function f : D → R is continuous on an interval I ⊆ D if it is con ...
ABCalc_Ch1_Notepacket 15-16
... x 2 ax, x 2 For what value of a is the function f x continuous at x = -2? 2 x 2, x 2 ...
... x 2 ax, x 2 For what value of a is the function f x continuous at x = -2? 2 x 2, x 2 ...
Cut Elimination
... We have to construct a proof of ∆, ∆0 ⇒ C, but ∆0 = (·) and C = A, so we can let F = D. In the remaining cases the last inference rule applied in the first or second premise of the cut must have been different from the cut formula. We call this a side formula. We organize the cases around which rule ...
... We have to construct a proof of ∆, ∆0 ⇒ C, but ∆0 = (·) and C = A, so we can let F = D. In the remaining cases the last inference rule applied in the first or second premise of the cut must have been different from the cut formula. We call this a side formula. We organize the cases around which rule ...
Introduction to Calculus
... This is the first volume of an introductory calculus presentation intended for future scientists and engineers. Volume I contains five chapters emphasizing fundamental concepts from calculus and analytic geometry and the application of these concepts to selected areas of science and engineering. Cha ...
... This is the first volume of an introductory calculus presentation intended for future scientists and engineers. Volume I contains five chapters emphasizing fundamental concepts from calculus and analytic geometry and the application of these concepts to selected areas of science and engineering. Cha ...
08_Functional
... Functional programs puts this model into practice: programs are written in terms of a sequence of functions, typically with nested evaluation: P(input) = (F(g(h(input))) U ... ) ...
... Functional programs puts this model into practice: programs are written in terms of a sequence of functions, typically with nested evaluation: P(input) = (F(g(h(input))) U ... ) ...