Quick Review of the Definition of the Definite Integral
... function is the function itself. If we combine this with part 1 of the Fundamental Theorem of Calculus which says that the derivative of the integral of a function is the function itself, we see that integration and di¤erentiation are inverse processes. One undoes what the other one does. If we comb ...
... function is the function itself. If we combine this with part 1 of the Fundamental Theorem of Calculus which says that the derivative of the integral of a function is the function itself, we see that integration and di¤erentiation are inverse processes. One undoes what the other one does. If we comb ...
Annotation-Free Sequent Calculi for Full Intuitionistic Linear Logic
... without the required annotations, making it unsound, and also contains other transcription errors. The second [16] identifies FILL with ‘Bi-Linear Logic’, which fails weak distributivity and has an extra connective called ‘exclusion’, of which more shortly. The existing correct annotated sequent cal ...
... without the required annotations, making it unsound, and also contains other transcription errors. The second [16] identifies FILL with ‘Bi-Linear Logic’, which fails weak distributivity and has an extra connective called ‘exclusion’, of which more shortly. The existing correct annotated sequent cal ...
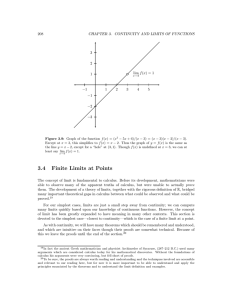
3.4 Finite Limits at Points
... For instance it reflects the fact that the limit has a built-in blind spot (by definition) at the point x = a. Also apparent is the local nature of limits: the fact that f and g could be wildly different farther away from x = a, i.e., for |x − a| ≥ d, is of no importance to the limit. The most commo ...
... For instance it reflects the fact that the limit has a built-in blind spot (by definition) at the point x = a. Also apparent is the local nature of limits: the fact that f and g could be wildly different farther away from x = a, i.e., for |x − a| ≥ d, is of no importance to the limit. The most commo ...
Mathematics 110 Laboratory Manual
... The same is true of mathematics. One does not learn mathematics by only reading a textbook and listening to lectures. Rather, one learns mathematics by doing mathematics. This Laboratory Manual is a set of problems that are representative of the types of problems that students of Mathematics 110 (Ca ...
... The same is true of mathematics. One does not learn mathematics by only reading a textbook and listening to lectures. Rather, one learns mathematics by doing mathematics. This Laboratory Manual is a set of problems that are representative of the types of problems that students of Mathematics 110 (Ca ...
Complete Sequent Calculi for Induction and Infinite Descent
... the locally applicable proof rules thereby constrained by the logical constants appearing in the current goal. In a previous paper by the first author [2], Gentzen’s LK was extended to obtain two proof systems for classical first-order logic with inductively defined predicates: (i) a system containi ...
... the locally applicable proof rules thereby constrained by the logical constants appearing in the current goal. In a previous paper by the first author [2], Gentzen’s LK was extended to obtain two proof systems for classical first-order logic with inductively defined predicates: (i) a system containi ...
Chapter 10: Logs and Exponential Functions
... It can be shown that this sequence of real numbers will approach a limit, and that limit is defined to be the value of 2 2 . There are many other sequences of rational numbers that approach 2 and it can be shown that if we raise 2 to each of them we’ll get a sequence that approaches the same limit a ...
... It can be shown that this sequence of real numbers will approach a limit, and that limit is defined to be the value of 2 2 . There are many other sequences of rational numbers that approach 2 and it can be shown that if we raise 2 to each of them we’ll get a sequence that approaches the same limit a ...
10. log and exponential functions
... Now differentiate both sides. This raises the question of whether it’s permissible to differentiate an infinite sum term by term just like we do for a finite sum. But because we don’t want to get embroiled in technical difficulties we’ll suppose that we can. There are some restrictions on when this ...
... Now differentiate both sides. This raises the question of whether it’s permissible to differentiate an infinite sum term by term just like we do for a finite sum. But because we don’t want to get embroiled in technical difficulties we’ll suppose that we can. There are some restrictions on when this ...
Section 1.4: Combinations of Functions
... To find the tax on a $2 can of stew, we would use the first piece of the rule and find that the tax is 0. To find the tax on a $30 pair of earrings, we would use the second piece of the rule and find that the tax is $3.60 . The tax on a $20 book requires using the third rule, and the tax is $1.20 . ...
... To find the tax on a $2 can of stew, we would use the first piece of the rule and find that the tax is 0. To find the tax on a $30 pair of earrings, we would use the second piece of the rule and find that the tax is $3.60 . The tax on a $20 book requires using the third rule, and the tax is $1.20 . ...
Test - FloridaMAO
... 11. Even though he wasn’t my coach, Mr. Propert was disappointed in me when I missed the question about the rational function’s asymptotes because one was a removable discontinuity. He said, “The factor that causes you to get zero over zero is a removable x2 x 2 discontinuity; a hole, which isn’ ...
... 11. Even though he wasn’t my coach, Mr. Propert was disappointed in me when I missed the question about the rational function’s asymptotes because one was a removable discontinuity. He said, “The factor that causes you to get zero over zero is a removable x2 x 2 discontinuity; a hole, which isn’ ...
Cyclic Proofs for First-Order Logic with Inductive Definitions
... Our aim is to study cyclic reasoning in the relatively simple, yet expressive context of first-order logic extended with ordinary inductive definitions1 . Similar formalisms typically form the basis of mechanised theorem proving tools [2, 8, 10, 13]. The contribution of this paper is twofold. Firstl ...
... Our aim is to study cyclic reasoning in the relatively simple, yet expressive context of first-order logic extended with ordinary inductive definitions1 . Similar formalisms typically form the basis of mechanised theorem proving tools [2, 8, 10, 13]. The contribution of this paper is twofold. Firstl ...
CHAP09 Logs and Exponentials
... It seems reasonable to assume that as the value of a increases from 2 to 3 then k increases from 0.69334 to 1,09922, and that it does so in a continuous fashion. So we would expect that somewhere between a = 2 and a = 3 the value of k becomes exactly equal to 1. For this value of a it will be the ca ...
... It seems reasonable to assume that as the value of a increases from 2 to 3 then k increases from 0.69334 to 1,09922, and that it does so in a continuous fashion. So we would expect that somewhere between a = 2 and a = 3 the value of k becomes exactly equal to 1. For this value of a it will be the ca ...
Certified Proof Search for Intuitionistic Linear Logic
... Type theory [16] equipped with inductive families [9] is expressive enough that one can implement certified proof search algorithms which are not merely oracles outputting a one bit answer but fullblown automated provers producing derivations which are statically known to be correct [5, 19]. It is on ...
... Type theory [16] equipped with inductive families [9] is expressive enough that one can implement certified proof search algorithms which are not merely oracles outputting a one bit answer but fullblown automated provers producing derivations which are statically known to be correct [5, 19]. It is on ...
Graph-Based Proof Counting and Enumeration with Applications for
... We are grateful to Christian Haack, Daniel Hirschkoff, and the anonymous referees for their helpful comments on earlier versions. ...
... We are grateful to Christian Haack, Daniel Hirschkoff, and the anonymous referees for their helpful comments on earlier versions. ...
Rocket-Fast Proof Checking for SMT Solvers
... where xij are additional technical arguments, to fulfill the condition that the left-hand side of a rule has to contains all the free variables in the right-hand side and r is a function symbol used to encode this particular rule. Therefore we can model (mp), (absurd) and (nnpp) using the rewrite rul ...
... where xij are additional technical arguments, to fulfill the condition that the left-hand side of a rule has to contains all the free variables in the right-hand side and r is a function symbol used to encode this particular rule. Therefore we can model (mp), (absurd) and (nnpp) using the rewrite rul ...
Primitive and General Recursive Functions
... We know that x 7→ 3 and x 7→ x2 are p.r., but is f also p.r.? We want to show that definition by cases is admissible in the sense that when applied to primitive recursive functions/relations we obtain another primitive recursive function. ...
... We know that x 7→ 3 and x 7→ x2 are p.r., but is f also p.r.? We want to show that definition by cases is admissible in the sense that when applied to primitive recursive functions/relations we obtain another primitive recursive function. ...
MAT 1015 Calculus I 2010/2011 John F. Rayman
... The latter three books are very comprehensive and cover all the calculus you are likely to need for your degree. ...
... The latter three books are very comprehensive and cover all the calculus you are likely to need for your degree. ...
CENTRAL LIMIT THEOREMS AND QUADRATIC VARIATIONS IN
... particular when one considers a weighted projection of a self-similar random field. We develop here methods that reveal to be stable when adding such a perturbation to the spectral density. A source of inspiration for us has also been the paper of Chan and Wood [8], which deals with stationary rando ...
... particular when one considers a weighted projection of a self-similar random field. We develop here methods that reveal to be stable when adding such a perturbation to the spectral density. A source of inspiration for us has also been the paper of Chan and Wood [8], which deals with stationary rando ...
6.5 Second Trigonometric Rules
... x sin x2 dx. 26 In a typical calculus class, the professor usually has to answer the question of why students have to learn all of the difficult integration techniques when there are references available. The answer is several-fold, and we make just a few points addressing it here. First, many probl ...
... x sin x2 dx. 26 In a typical calculus class, the professor usually has to answer the question of why students have to learn all of the difficult integration techniques when there are references available. The answer is several-fold, and we make just a few points addressing it here. First, many probl ...
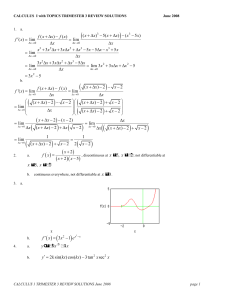
Continuity and one
... has a jump discontinuity at x=-2 b) To decide the continuity in its entirety, it is needed to check each function´s continuity. The first function, f ( x) 2x 1 for x , 2 is continuous in its entirety of domain, the second function f ( x) 1 x2 for x 2, 2 also is continuous in it ...
... has a jump discontinuity at x=-2 b) To decide the continuity in its entirety, it is needed to check each function´s continuity. The first function, f ( x) 2x 1 for x , 2 is continuous in its entirety of domain, the second function f ( x) 1 x2 for x 2, 2 also is continuous in it ...
Convex Programming - Santa Fe Institute
... A subset C of a Euclidean space is convex if it contains the line segment connecting any two of its members. That is, if x and y are vectors in C and t is a number between 0 and 1, the vector tx + (1 − t)y is also in C. A linear combination with non-negative weights which sum to 1 is a convex combin ...
... A subset C of a Euclidean space is convex if it contains the line segment connecting any two of its members. That is, if x and y are vectors in C and t is a number between 0 and 1, the vector tx + (1 − t)y is also in C. A linear combination with non-negative weights which sum to 1 is a convex combin ...
APEX Calculus I
... Rates of change were also important. When an object moves at a constant rate of change, then “distance = rate × time.” But what if the rate is not constant – can distance still be computed? Or, if distance is known, can we discover the rate of change? It turns out that these two concepts were relate ...
... Rates of change were also important. When an object moves at a constant rate of change, then “distance = rate × time.” But what if the rate is not constant – can distance still be computed? Or, if distance is known, can we discover the rate of change? It turns out that these two concepts were relate ...
There are three most common inverse trigonometric functions
... The inverse cosine function is written as y = cos−1 (x) or y = arccos x. (Not to be confused with y = 1/ cos x.) The domain of arccos x is the interval [−1, 1] and its range is [0, π]. For any number x between −1 and 1, arccos x is the angle between 0 and π whose cosine is x. In other words, let −1 ...
... The inverse cosine function is written as y = cos−1 (x) or y = arccos x. (Not to be confused with y = 1/ cos x.) The domain of arccos x is the interval [−1, 1] and its range is [0, π]. For any number x between −1 and 1, arccos x is the angle between 0 and π whose cosine is x. In other words, let −1 ...