calcuLec11 - United International College
... Newton's own first edition copy of his Philosophiae Naturalis Principia Mathematica with his handwritten corrections for the second edition. The book can be seen in the Wren Library of Trinity College, Cambridge. ...
... Newton's own first edition copy of his Philosophiae Naturalis Principia Mathematica with his handwritten corrections for the second edition. The book can be seen in the Wren Library of Trinity College, Cambridge. ...
Multidimensional Calculus. Lectures content. Week 10 22. Tests for
... Definition. Let {fk }k≥n0 , f be functions on a set M . We say that {fk } converges uniformly to f on M , denoted fk → →f , if ∀ε > 0∃N0 ∈ IN such that ∀k ≥ N0 ∀x ∈ M : |f (x) − fk (x)| < ε. Theorem. Let fk → →f on M . (i) If all fk are continuous on M , then also f is continuous there. (ii) If all ...
... Definition. Let {fk }k≥n0 , f be functions on a set M . We say that {fk } converges uniformly to f on M , denoted fk → →f , if ∀ε > 0∃N0 ∈ IN such that ∀k ≥ N0 ∀x ∈ M : |f (x) − fk (x)| < ε. Theorem. Let fk → →f on M . (i) If all fk are continuous on M , then also f is continuous there. (ii) If all ...
x - United International College
... The book can be seen in the Wren Library of Trinity College, Cambridge. ...
... The book can be seen in the Wren Library of Trinity College, Cambridge. ...
Notes on Calculus II Integral Calculus Miguel A. Lerma
... small amounts f (x) dx. The symbol dx was interpreted as the length of an “infinitesimal” interval, sort of what ∆x becomes for infinite n. This interpretation was later abandoned due to the difficulty of reasoning with infinitesimals, but we keep the notation. Remark : Note that in intervals where ...
... small amounts f (x) dx. The symbol dx was interpreted as the length of an “infinitesimal” interval, sort of what ∆x becomes for infinite n. This interpretation was later abandoned due to the difficulty of reasoning with infinitesimals, but we keep the notation. Remark : Note that in intervals where ...
Subtraction of Convex Sets and Its Application in E
... Nurminski, E.A. (1982) Subtraction of Convex Sets and Its Application in E-Subdifferential Calculus. IIASA Working Paper. IIASA, Laxenburg, Austria, WP-82-083 Copyright © 1982 by the author(s). http://pure.iiasa.ac.at/1933/ Working Papers on work of the International Institute for Applied Systems A ...
... Nurminski, E.A. (1982) Subtraction of Convex Sets and Its Application in E-Subdifferential Calculus. IIASA Working Paper. IIASA, Laxenburg, Austria, WP-82-083 Copyright © 1982 by the author(s). http://pure.iiasa.ac.at/1933/ Working Papers on work of the International Institute for Applied Systems A ...
CSC321 Lecture 2: Linear Regression
... Linear regression is one of only a handful of models in this course that ...
... Linear regression is one of only a handful of models in this course that ...
ppt
... Since all of the above limits exist and are finite, f cannot have a vertical asymptote at x = a. In order for f to have a vertical asymptote at x = a, at least one of the limits above must be an infinite limit, and f must be discontinuous at x = a. We know that polynomial functions are continuous fo ...
... Since all of the above limits exist and are finite, f cannot have a vertical asymptote at x = a. In order for f to have a vertical asymptote at x = a, at least one of the limits above must be an infinite limit, and f must be discontinuous at x = a. We know that polynomial functions are continuous fo ...
Hammack 5: Logarithm Review
... 5.1 Review of Exponents We start at the beginning. For a number a and a positive integer n, a n = |a · a ·{z a · · · a} . ...
... 5.1 Review of Exponents We start at the beginning. For a number a and a positive integer n, a n = |a · a ·{z a · · · a} . ...
Mathematica
... Apply[f,expr] replaces the head of expr by f and evaluates it Map[f,list] applies the function f to each element of list Nest[f,expr,n] gives an expression with f applied n times to expr NestList[f,expr,n] does the same but returns the list of all intermediate results ...
... Apply[f,expr] replaces the head of expr by f and evaluates it Map[f,list] applies the function f to each element of list Nest[f,expr,n] gives an expression with f applied n times to expr NestList[f,expr,n] does the same but returns the list of all intermediate results ...
Mathematica
... Apply[f,expr] replaces the head of expr by f and evaluates it Map[f,list] applies the function f to each element of list Nest[f,expr,n] gives an expression with f applied n times to expr NestList[f,expr,n] does the same but returns the list of all intermediate results ...
... Apply[f,expr] replaces the head of expr by f and evaluates it Map[f,list] applies the function f to each element of list Nest[f,expr,n] gives an expression with f applied n times to expr NestList[f,expr,n] does the same but returns the list of all intermediate results ...
Part 1 - CSUN.edu
... Proposition 3 Let A ⊂ R be bounded above. Then the following statements are equivalent: 1. M = sup A. 2. M is an upper bound of A and for every ε > 0 there is an a ∈ A such that M − ε < a ≤ M . Proof: Suppose M = sup A, and suppose that there is a number ε0 > 0 such that a ≤ M − ε0 for all a ∈ A. Th ...
... Proposition 3 Let A ⊂ R be bounded above. Then the following statements are equivalent: 1. M = sup A. 2. M is an upper bound of A and for every ε > 0 there is an a ∈ A such that M − ε < a ≤ M . Proof: Suppose M = sup A, and suppose that there is a number ε0 > 0 such that a ≤ M − ε0 for all a ∈ A. Th ...
1 Derivatives of trigonometric functions
... This derivative will be zero when cos2 (θ) = sin2 (θ) or sin(θ) = ± cos(θ). Since θ is an acute angle, the solution must be θ = π/4. Example. If f (x) = sin(x) + cos(x), find the derivative f (401) (x). Can you find a function f which satisfies f 00 + f = 0? Can each member of the class find a diffe ...
... This derivative will be zero when cos2 (θ) = sin2 (θ) or sin(θ) = ± cos(θ). Since θ is an acute angle, the solution must be θ = π/4. Example. If f (x) = sin(x) + cos(x), find the derivative f (401) (x). Can you find a function f which satisfies f 00 + f = 0? Can each member of the class find a diffe ...
(pdf)
... Definition 2.4. (Equivalence Modulo an Ultrafilter) Given a free ultrafilter U on N, and real-valued sequences a, b ∈ RN , we define the relation =U by a =U b if {j ∈ N|aj = bj } ∈ U We now show that this is an equivalence relation. For reflexivity, take any sequence a. We have {j ∈ N|aj = aj } = N, ...
... Definition 2.4. (Equivalence Modulo an Ultrafilter) Given a free ultrafilter U on N, and real-valued sequences a, b ∈ RN , we define the relation =U by a =U b if {j ∈ N|aj = bj } ∈ U We now show that this is an equivalence relation. For reflexivity, take any sequence a. We have {j ∈ N|aj = aj } = N, ...
Problem Points Score Problem Points Score 1 10 6 13 2 17 7 27 3
... 1. Show your University of Pittsburgh ID if requested. 2. Clearly print your name and PeopleSoft number and sign your name in the space above. Circle the name of your lecturer and the time of your lecture. 3. Work each problem in the space provided. Extra space is available on the back of each exam ...
... 1. Show your University of Pittsburgh ID if requested. 2. Clearly print your name and PeopleSoft number and sign your name in the space above. Circle the name of your lecturer and the time of your lecture. 3. Work each problem in the space provided. Extra space is available on the back of each exam ...
1 Derivatives of trigonometric functions
... This derivative will be zero when cos2 (θ) = sin2 (θ) or sin(θ) = ± cos(θ). Since θ is an acute angle, the solution must be θ = π/4. Example. If f (x) = sin(x) + cos(x), find the derivative f (401) (x). Can you find a function f which satisfies f 00 + f = 0? Can each member of the class find a diffe ...
... This derivative will be zero when cos2 (θ) = sin2 (θ) or sin(θ) = ± cos(θ). Since θ is an acute angle, the solution must be θ = π/4. Example. If f (x) = sin(x) + cos(x), find the derivative f (401) (x). Can you find a function f which satisfies f 00 + f = 0? Can each member of the class find a diffe ...
Calculus 1 Syllabus
... Academic Expectations: Classwork - You are expected to attend class regularly and take notes. Please note that there are no make-up quiz or exams scheduled. If you miss an exam (does not apply for quiz), and if you promptly provide me, in writing, a verifiable & acceptable excuse for your absence, ...
... Academic Expectations: Classwork - You are expected to attend class regularly and take notes. Please note that there are no make-up quiz or exams scheduled. If you miss an exam (does not apply for quiz), and if you promptly provide me, in writing, a verifiable & acceptable excuse for your absence, ...
Analysis of Functions: Increase, Decrease, and Concavity Solutions
... (b) If f and g are increasing on an interval, then so is f · g. This is a trick question in that there are two cases... Case I: True if f and g are both positive, increasing functions, i.e. if 0 < f (x1 ) < f (x2 ) and 0 < g(x1 ) < g(x2 ) for x1 < x2 , where x1 , x2 in some interval I, then it follo ...
... (b) If f and g are increasing on an interval, then so is f · g. This is a trick question in that there are two cases... Case I: True if f and g are both positive, increasing functions, i.e. if 0 < f (x1 ) < f (x2 ) and 0 < g(x1 ) < g(x2 ) for x1 < x2 , where x1 , x2 in some interval I, then it follo ...
Calculus Fall 2010 Lesson 05 _Evaluating limits of
... 1) Students will be able to evaluate limits by rationalizing either the numerator or denominator of a function. 2) Students will be able to evaluate limits of functions that are expressed as complex fractions, by simplifying the complex fraction into a simple fraction. 3) Students will be able to ev ...
... 1) Students will be able to evaluate limits by rationalizing either the numerator or denominator of a function. 2) Students will be able to evaluate limits of functions that are expressed as complex fractions, by simplifying the complex fraction into a simple fraction. 3) Students will be able to ev ...
MODULE 21 Topics: ez, sinz, cosz, log(z) and z Now that we have
... may be thought of as the extension of the identity function f (x) = x to the complex plane. However, we shall always require that the complex valued function be differentiable at all x where f as a function of x is differentiable. It turns out that this makes the extension unique. For example, f (z) ...
... may be thought of as the extension of the identity function f (x) = x to the complex plane. However, we shall always require that the complex valued function be differentiable at all x where f as a function of x is differentiable. It turns out that this makes the extension unique. For example, f (z) ...
Solutions to In-Class Work Let f(x) = cos(x) − sin(x) g(x)=4ex − 3 cos
... is m, the line has the form mx + b – but we don’t worry about those pesky additive constants here. So the antiderivative of 3 sin(4) is just 3 sin(4) · x. • When we differentiated 2 sin(3x), we got 3 · 2 cos(3x). This time we’re antidifferentiating. What do we get? Just go ahead and guess, and then ...
... is m, the line has the form mx + b – but we don’t worry about those pesky additive constants here. So the antiderivative of 3 sin(4) is just 3 sin(4) · x. • When we differentiated 2 sin(3x), we got 3 · 2 cos(3x). This time we’re antidifferentiating. What do we get? Just go ahead and guess, and then ...
SAMPLE Final Exam: Comprehensive Part
... 6. (a) (5 pts) Bismuth-210 is a radioactive substance whose mass decays exponentially. It has a half-life of 5.0 days. A sample originally has a mass of 800 mg. Find a formula for the mass y(t) remaining after t days. (b) ...
... 6. (a) (5 pts) Bismuth-210 is a radioactive substance whose mass decays exponentially. It has a half-life of 5.0 days. A sample originally has a mass of 800 mg. Find a formula for the mass y(t) remaining after t days. (b) ...
Math 55b Lecture Notes Contents
... distance between two vertices to be the graph-theoretic distance between them. (The discrete metric is the special case when G is the complete graph on S.) ...
... distance between two vertices to be the graph-theoretic distance between them. (The discrete metric is the special case when G is the complete graph on S.) ...
The Inverse Trigonometric Functions - Beck-Shop
... of inverse trigonometric functions. This theory is complicated by the fact that the trigonometric functions are periodic functions — they therefore fail the horizontal line test quite seriously, in that some horizontal lines cross their graphs infinitely many times. Understanding inverse trigonometri ...
... of inverse trigonometric functions. This theory is complicated by the fact that the trigonometric functions are periodic functions — they therefore fail the horizontal line test quite seriously, in that some horizontal lines cross their graphs infinitely many times. Understanding inverse trigonometri ...
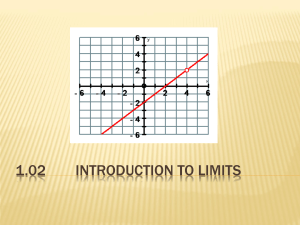
Limits - hrsbstaff.ednet.ns.ca
... A limit is the intended value of a function. It is the value which f(x) gets close to as "x" gets close to "a". SOMETIMES this limit is just f(a) but NOT always. ...
... A limit is the intended value of a function. It is the value which f(x) gets close to as "x" gets close to "a". SOMETIMES this limit is just f(a) but NOT always. ...