Lecture 2: Entropy and mutual information
... Note that an analogue of Jensen’s inequality exists for concave functions where the inequality simply changes sign. Relative entropy A very natural way to measure the distance between two probability distributions is the relative entropy, also sometimes called the Kullback-Leibler divergence. Defini ...
... Note that an analogue of Jensen’s inequality exists for concave functions where the inequality simply changes sign. Relative entropy A very natural way to measure the distance between two probability distributions is the relative entropy, also sometimes called the Kullback-Leibler divergence. Defini ...
MA11001 Calculus Workshop 4 Week 8, Answers
... 6. In each case determine whether the function f is one-to-one by investigating the sign of f v ÝxÞ. a. fÝxÞ = x 2 + 8x + 7, f v Ý x Þ = 2x + 8 changes sign at x = ?4, so f cannot be one–to–one. b. fÝxÞ = 5x 7 + 3x 3 + 17x ? 9, f v Ý x Þ = 35x 6 + 9x 2 + 17 > 0 and so f is an increasing function—it ...
... 6. In each case determine whether the function f is one-to-one by investigating the sign of f v ÝxÞ. a. fÝxÞ = x 2 + 8x + 7, f v Ý x Þ = 2x + 8 changes sign at x = ?4, so f cannot be one–to–one. b. fÝxÞ = 5x 7 + 3x 3 + 17x ? 9, f v Ý x Þ = 35x 6 + 9x 2 + 17 > 0 and so f is an increasing function—it ...
Lecture notes
... The x-intercept of a line is the point at which the line crosses the x axis. ( i.e. where the y value equals 0 ) x − intercept =(x , 0) The y-intercept of a line is the point at which the line crosses the y axis. ( i.e. where the x value equals 0 ) ...
... The x-intercept of a line is the point at which the line crosses the x axis. ( i.e. where the y value equals 0 ) x − intercept =(x , 0) The y-intercept of a line is the point at which the line crosses the y axis. ( i.e. where the x value equals 0 ) ...
3.3 Printable - WordPress.com
... Derivatives of sin and cos graphically Let’s look at the graphs of y = sin x and y = cos x and attempt to take the derivatives of these functions graphically. The graph of the derivative of y = sin x looks an awful lot like the graph of y = cos x. The graph of the derivative of y = cos x looks like ...
... Derivatives of sin and cos graphically Let’s look at the graphs of y = sin x and y = cos x and attempt to take the derivatives of these functions graphically. The graph of the derivative of y = sin x looks an awful lot like the graph of y = cos x. The graph of the derivative of y = cos x looks like ...
Math 500 – Intermediate Analysis Homework 8 – Solutions
... of convergence for this power series is − 65 , 56 . 24.2 For x ∈ [0, ∞), let fn (x) = nx . (a) Find f (x) = limn→∞ fn (x). Solution: For a given x0 ∈ [0, ∞), the numerical sequence fn (x0 ) = xn0 clearly converges to zero as n → ∞. Thus, the sequence of functions (fn ) converges pointwise to the fun ...
... of convergence for this power series is − 65 , 56 . 24.2 For x ∈ [0, ∞), let fn (x) = nx . (a) Find f (x) = limn→∞ fn (x). Solution: For a given x0 ∈ [0, ∞), the numerical sequence fn (x0 ) = xn0 clearly converges to zero as n → ∞. Thus, the sequence of functions (fn ) converges pointwise to the fun ...
Chapter 4 Section 9 - Columbus State University
... might wish to know its position at a given time. An engineer who can measure the variable rate at which water is leaking from a tank wants to know the amount leaked over a certain time period. A biologist who knows the rate at which a bacteria population is increasing might want to deduce what the s ...
... might wish to know its position at a given time. An engineer who can measure the variable rate at which water is leaking from a tank wants to know the amount leaked over a certain time period. A biologist who knows the rate at which a bacteria population is increasing might want to deduce what the s ...
An alternate approach to changing sine
... the sine of a sum. While there is some variation in the texts as to how the first limit is obtained using geometry, the final steps using a trigonometric identity and applying both limits is common. Our goal here is to present an alternative approach for the derivative of sine with the idea that it ...
... the sine of a sum. While there is some variation in the texts as to how the first limit is obtained using geometry, the final steps using a trigonometric identity and applying both limits is common. Our goal here is to present an alternative approach for the derivative of sine with the idea that it ...
10.2
... A constant function is continuous for all x. For integer n > 0, f (x) = xn is continuous for all x. A polynomial function is continuous for all x. A rational function is continuous for all x, except those values that make the denominator 0. For n an odd positive integer, n f ( x) is continuous whe ...
... A constant function is continuous for all x. For integer n > 0, f (x) = xn is continuous for all x. A polynomial function is continuous for all x. A rational function is continuous for all x, except those values that make the denominator 0. For n an odd positive integer, n f ( x) is continuous whe ...
For a rational function f(x) = p(x) / q(x), where p(x)
... set-builder notation for the solution set. If the inequality symbol “or equal to” is used, then the solutions to step 2 and 3 should be included. The x-values found in step 3 are NEVER included in the solution set. ...
... set-builder notation for the solution set. If the inequality symbol “or equal to” is used, then the solutions to step 2 and 3 should be included. The x-values found in step 3 are NEVER included in the solution set. ...
Calculus I: Section 1.3 Intuitive Limits
... and say, “The limit of f (x) as x approaches a equals L,” if we can make the values of f (x) arbitrarily close to L by taking x to be sufficiently close to a on either side of a but not equal to a. This says that the values of f (x) tend to come closer to L as x comes closer and closer to a from eit ...
... and say, “The limit of f (x) as x approaches a equals L,” if we can make the values of f (x) arbitrarily close to L by taking x to be sufficiently close to a on either side of a but not equal to a. This says that the values of f (x) tend to come closer to L as x comes closer and closer to a from eit ...
Transcript - MIT OpenCourseWare
... So here, for example, in part a, I've given you the function f of x, y equal to x squared y plus xy squared, at the point x equal minus 1, y equal 2, and in the direction of the vector 3, 4. And then we've got two more examples here. g of x, y, z is equal to the square root of x squared plus y squar ...
... So here, for example, in part a, I've given you the function f of x, y equal to x squared y plus xy squared, at the point x equal minus 1, y equal 2, and in the direction of the vector 3, 4. And then we've got two more examples here. g of x, y, z is equal to the square root of x squared plus y squar ...
Lecture 8: Quadratic variation
... where the supremum is taken over all possible partitions Π of the interval [0, T ] for all n. A function f is defined to have bounded variation if its total variation is finite. Theorem 1. Almost surely no path of a Brownian motion has bounded variation for every T ≥ 0. Namely, for every T P(ω : LV (B ...
... where the supremum is taken over all possible partitions Π of the interval [0, T ] for all n. A function f is defined to have bounded variation if its total variation is finite. Theorem 1. Almost surely no path of a Brownian motion has bounded variation for every T ≥ 0. Namely, for every T P(ω : LV (B ...
Chapter 12 Infinite series, improper integrals, and Taylor series
... In studying calculus, we have explored a variety of functions. Among the most basic are polynomials, i.e. functions such as p(x) = x5 + 2x2 + 3x + 2. These functions have features that make them particularly easy to handle: it is elementary to compute the derivatives and integrals of polynomials. Fu ...
... In studying calculus, we have explored a variety of functions. Among the most basic are polynomials, i.e. functions such as p(x) = x5 + 2x2 + 3x + 2. These functions have features that make them particularly easy to handle: it is elementary to compute the derivatives and integrals of polynomials. Fu ...
Polynomial Functions
... The notion of smoothness is what tells us graphically that, for example, f (x) = |x|, whose graph is the characteristic ‘∨’ shape, cannot be a polynomial. The notion of continuity is what allowed us to construct the sign diagram for quadratic inequalities as we did in Section 2.4. This last result i ...
... The notion of smoothness is what tells us graphically that, for example, f (x) = |x|, whose graph is the characteristic ‘∨’ shape, cannot be a polynomial. The notion of continuity is what allowed us to construct the sign diagram for quadratic inequalities as we did in Section 2.4. This last result i ...
Test #2
... 15. The length l , width w and height h of a box change with time. At a certain instant the dimensions are l 2m and w h 3 and w and h are increasing at a rate of 3m / sec and l is decreasing at a rate of 1m / sec . At that instant find the rates at which the surface areas are changing. 16. The ...
... 15. The length l , width w and height h of a box change with time. At a certain instant the dimensions are l 2m and w h 3 and w and h are increasing at a rate of 3m / sec and l is decreasing at a rate of 1m / sec . At that instant find the rates at which the surface areas are changing. 16. The ...
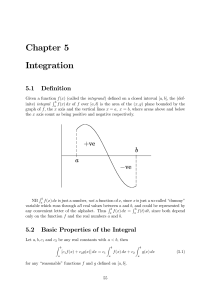
Chapter 5 Integration
... A primitive of f will henceforth be called an indefinite integral of f and written f (x) dx (without limits). This is a function of x, but it is determined only to within an arbitrary additive constant. Once we have an indefinite integral of f on some interval, we can immediately evaluate the defini ...
... A primitive of f will henceforth be called an indefinite integral of f and written f (x) dx (without limits). This is a function of x, but it is determined only to within an arbitrary additive constant. Once we have an indefinite integral of f on some interval, we can immediately evaluate the defini ...
Developing the Calculus
... Observe that, using purely geometric methods, Barrow was able to arrive at this conclusion. He did not actually use the functional notation, nor did he realize the importance of the calculations that he was making. Therefore, it is not proper to say that Barrow invented Calculus. He merely stumbled ...
... Observe that, using purely geometric methods, Barrow was able to arrive at this conclusion. He did not actually use the functional notation, nor did he realize the importance of the calculations that he was making. Therefore, it is not proper to say that Barrow invented Calculus. He merely stumbled ...
lecture - Dartmouth Math Home
... complement Y \ V is closed, as V is open. Thus f −1 (Y \ V ) is closed in X. But the preimage of the complement is the complement of the preimage, i.e. f −1 (Y \ V ) = f −1 (Y ) \ f −1 (V ). We can replace f −1 (Y ) with X, to obtain f −1 (Y \ V ) = X \ f −1 (V ). So X \ f −1 (V ) is closed, so that ...
... complement Y \ V is closed, as V is open. Thus f −1 (Y \ V ) is closed in X. But the preimage of the complement is the complement of the preimage, i.e. f −1 (Y \ V ) = f −1 (Y ) \ f −1 (V ). We can replace f −1 (Y ) with X, to obtain f −1 (Y \ V ) = X \ f −1 (V ). So X \ f −1 (V ) is closed, so that ...
SPACE-TIME FRACTIONAL DERIVATIVE OPERATORS 1
... In classical diffusion, particles spread in a normal bell-shaped pattern whose width grows like the square root of time. Anomalous diffusion occurs when the growth rate or the shape of the particle distribution is different than the classical model predicts. Anomalous diffusion is observed in many physi ...
... In classical diffusion, particles spread in a normal bell-shaped pattern whose width grows like the square root of time. Anomalous diffusion occurs when the growth rate or the shape of the particle distribution is different than the classical model predicts. Anomalous diffusion is observed in many physi ...
Essential Mathematics for Political and Social Research Jeff Gill
... mathematical training beyond this modest level. Furthermore, the first chapter is sufficiently basic that readers who are comfortable with only arithmetic operations on symbolic quantities will be able to work through the material. No prior knowledge of statistics, probability, or nonscalar represen ...
... mathematical training beyond this modest level. Furthermore, the first chapter is sufficiently basic that readers who are comfortable with only arithmetic operations on symbolic quantities will be able to work through the material. No prior knowledge of statistics, probability, or nonscalar represen ...