Remarkable Theorem
... number. But we did not define ay if y is irrational because this would have been an extremely difficult task without the use of calculus. We are now in a position where it is easy to define irrational exponents, and we must do so. [When a physicist or an engineering professor uses the function g(x) ...
... number. But we did not define ay if y is irrational because this would have been an extremely difficult task without the use of calculus. We are now in a position where it is easy to define irrational exponents, and we must do so. [When a physicist or an engineering professor uses the function g(x) ...
Math 432 - Real Analysis II
... which is incredibly small for use of such a small value of n. R1 (e) The questions asks us to compute −1 f (x) dx, which can be obtained by doubling the result from (c) since f (x) is an even function. Thus, the probability that a randomly chosen sample from a normally distributed data set will fall ...
... which is incredibly small for use of such a small value of n. R1 (e) The questions asks us to compute −1 f (x) dx, which can be obtained by doubling the result from (c) since f (x) is an even function. Thus, the probability that a randomly chosen sample from a normally distributed data set will fall ...
Section 2.1 Linear Functions
... 1. Determine the leading term. Is the degree even or odd? Is the leading coefficient positive or negative? Use the answers to both questions to determine the end behavior. 2. Find the y-intercept. 3. Factor the polynomial. 4. Find the x-intercept(s). 5. Plot the x-intercepts and y-intercept on the 2 ...
... 1. Determine the leading term. Is the degree even or odd? Is the leading coefficient positive or negative? Use the answers to both questions to determine the end behavior. 2. Find the y-intercept. 3. Factor the polynomial. 4. Find the x-intercept(s). 5. Plot the x-intercepts and y-intercept on the 2 ...
Precalculus
... Find the least common denominator among all fractions (if none already exists) Multiply each denominator by an appropriate factor to make it equivalent to the LCD Multiply each numerator by the same factor that you multiplied its denominator by Combine all numerators (make sure the signs are ...
... Find the least common denominator among all fractions (if none already exists) Multiply each denominator by an appropriate factor to make it equivalent to the LCD Multiply each numerator by the same factor that you multiplied its denominator by Combine all numerators (make sure the signs are ...
Week 2 - NUI Galway
... another. In this course, we are mainly concerned with functions D → R, where D ⊆ R. Functions occur in inequalities as problems of the form: For what values of x is f(x) > 0? Inequalities can also be used inside the definition of a function. This gives a piecewise defined function. The most importan ...
... another. In this course, we are mainly concerned with functions D → R, where D ⊆ R. Functions occur in inequalities as problems of the form: For what values of x is f(x) > 0? Inequalities can also be used inside the definition of a function. This gives a piecewise defined function. The most importan ...
Inverse Trigonometric Functions and their Derivatives
... (x) . (Both equations are true; often, one will be easier to work with than the other.) ...
... (x) . (Both equations are true; often, one will be easier to work with than the other.) ...
![(1) x 1]. - UBC Math](http://s1.studyres.com/store/data/014679358_1-e6d29f4b3cddfe3ae9f7c8c853ecf309-300x300.png)
(1) x 1]. - UBC Math
... three rectangles and right endpoints. Then improve your estimate by using 6 rectangles. Sketch the graph and the rectangles. (b) Repeat part (a) using left endpoints. ...
... three rectangles and right endpoints. Then improve your estimate by using 6 rectangles. Sketch the graph and the rectangles. (b) Repeat part (a) using left endpoints. ...
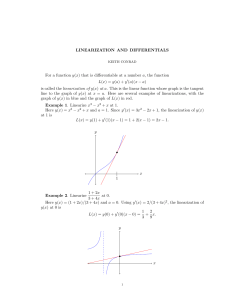
LINEARIZATION AND DIFFERENTIALS For a function y(x) that is
... is called the linearization of y(x) at a. This is the linear function whose graph is the tangent line to the graph of y(x) at x = a. Here are several examples of linearizations, with the graph of y(x) in blue and the graph of L(x) in red. Example 1. Linearize x3 − x2 + x at 1. Here y(x) = x3 − x2 + ...
... is called the linearization of y(x) at a. This is the linear function whose graph is the tangent line to the graph of y(x) at x = a. Here are several examples of linearizations, with the graph of y(x) in blue and the graph of L(x) in red. Example 1. Linearize x3 − x2 + x at 1. Here y(x) = x3 − x2 + ...
Test 2
... Solution. — a. If −1 < x < 1 and x , 0, then 1 + x < ex and (replacing x by −x) 1 − x < e−x , or ex < 1/(1 − x). Subtracting x yields x < ex − 1 < x/(1 − x), and then dividing by x and replacing x by x0 − x yields ...
... Solution. — a. If −1 < x < 1 and x , 0, then 1 + x < ex and (replacing x by −x) 1 − x < e−x , or ex < 1/(1 − x). Subtracting x yields x < ex − 1 < x/(1 − x), and then dividing by x and replacing x by x0 − x yields ...
4.1 Part 2 Particle Motion
... Let f be defined on the closed interval [a, b] and let be a partition of [a, b] given by a = x0 < x1 < x2 < . . . < xn - 1 < xn = b, where xi is the length of the ith subinterval. If ci is any point in the ith subinterval, then the sum ...
... Let f be defined on the closed interval [a, b] and let be a partition of [a, b] given by a = x0 < x1 < x2 < . . . < xn - 1 < xn = b, where xi is the length of the ith subinterval. If ci is any point in the ith subinterval, then the sum ...
Mathematical Explorations
... When higher derivatives are being used in the differential calculus the symbol F (n) is often used to denote the nth derivative of a function F . For the function T = tan(x) we know that T (1) = 1 + T 2 . Use the chain rule to work out the derivatives of tan(x) up to T (5) and show how this can give ...
... When higher derivatives are being used in the differential calculus the symbol F (n) is often used to denote the nth derivative of a function F . For the function T = tan(x) we know that T (1) = 1 + T 2 . Use the chain rule to work out the derivatives of tan(x) up to T (5) and show how this can give ...
R`(x)
... is given by C’(x) = 1.064 – 0.005x, find the total cost function if fixed cost is 16.3. ...
... is given by C’(x) = 1.064 – 0.005x, find the total cost function if fixed cost is 16.3. ...
1.2 Elementary functions and graph
... functions by a finite number of rational operations and compositions of functions which can be expressed by a single analytic expression is called an elementary functions. Notations ...
... functions by a finite number of rational operations and compositions of functions which can be expressed by a single analytic expression is called an elementary functions. Notations ...
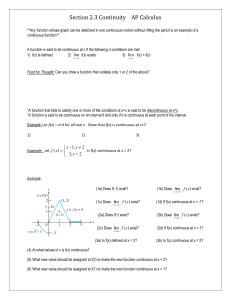
Section 2.3 Continuity AP Calculus - AP Calculus
... Theorem: If f(x) is continuous on a closed interval [a, b] and f(a) f(b), then for every value M between f(a) and f(b), there exists at least one value c (a, b) such that f(c) = M. *Corollary: If f(x) is continuous on [a, b] and if f(a) and f(b) are nonzero and have opposite signs, then f(x) has ...
... Theorem: If f(x) is continuous on a closed interval [a, b] and f(a) f(b), then for every value M between f(a) and f(b), there exists at least one value c (a, b) such that f(c) = M. *Corollary: If f(x) is continuous on [a, b] and if f(a) and f(b) are nonzero and have opposite signs, then f(x) has ...
dv dt = dr dt r(t)
... Plot at the point corresponding to time t Tail at (x(t), y(t), z(t)) Tip points tangent to the curve in the direction of the motion ...
... Plot at the point corresponding to time t Tail at (x(t), y(t), z(t)) Tip points tangent to the curve in the direction of the motion ...
dx - TaMATHawis!
... What you are finding: You are looking at problems in the form of " f (t) dt . This is asking for the rate dx a of change with respect to x of the accumulation function starting at some constant (which is irrelevant) and ending at that variable x. It is important to understand that this expression is ...
... What you are finding: You are looking at problems in the form of " f (t) dt . This is asking for the rate dx a of change with respect to x of the accumulation function starting at some constant (which is irrelevant) and ending at that variable x. It is important to understand that this expression is ...
MORE ON VERTICAL TANGENT LINES 1. Introduction In Thomas
... Question: Suppose that a function f is differentiable on (a, x0 ) and also differentiable on (x0 , b), and also continuous at the point x0 . Then is it true that f has a vertical tangent at x0 if and only if one of the following two things occurs? lim f 0 (x) = ∞ or lim f 0 (x) = −∞ ...
... Question: Suppose that a function f is differentiable on (a, x0 ) and also differentiable on (x0 , b), and also continuous at the point x0 . Then is it true that f has a vertical tangent at x0 if and only if one of the following two things occurs? lim f 0 (x) = ∞ or lim f 0 (x) = −∞ ...
f(x)
... 13) Is f defined at x = 2 ? Is f continuous at x = 2? 14) At what values of x is f continuous? 15) What value should be assigned to f(2) to make the extended function continuous at x = 2 . 16) What new value should be assigned to f(1) to make the extended function continuous at x = 1 . 17) Is it pos ...
... 13) Is f defined at x = 2 ? Is f continuous at x = 2? 14) At what values of x is f continuous? 15) What value should be assigned to f(2) to make the extended function continuous at x = 2 . 16) What new value should be assigned to f(1) to make the extended function continuous at x = 1 . 17) Is it pos ...
22M:16 Fall 05 J. Simon Introduction to Differential Equations
... [NOTE: We have not yet developed the machinery to know when we have **all** possible solutions. So for now, the phrase "general solution" will just mean an infinite family of solutions corresponding to one or more constants that can be chosen arbitrarily.] Solution for Example 4: We want a function ...
... [NOTE: We have not yet developed the machinery to know when we have **all** possible solutions. So for now, the phrase "general solution" will just mean an infinite family of solutions corresponding to one or more constants that can be chosen arbitrarily.] Solution for Example 4: We want a function ...
![MATH 409, Fall 2013 [3mm] Advanced Calculus I](http://s1.studyres.com/store/data/019184906_1-2ea198de2d20e978c4b1d91fadeb6dab-300x300.png)
MATH 409, Fall 2013 [3mm] Advanced Calculus I
... interval [a, b] is also uniformly continuous on [a, b]. Proof: Assume that a function f : [a, b] → R is not uniformly continuous on [a, b]. We have to show that f is not continuous on [a, b]. By assumption, there exists ε > 0 such that for any δ > 0 we can find two points x, y ∈ [a, b] satisfying |x ...
... interval [a, b] is also uniformly continuous on [a, b]. Proof: Assume that a function f : [a, b] → R is not uniformly continuous on [a, b]. We have to show that f is not continuous on [a, b]. By assumption, there exists ε > 0 such that for any δ > 0 we can find two points x, y ∈ [a, b] satisfying |x ...