Document
... As the function f(x) = (ln x)/x in the example is positive for x > 1, the integral represents the area of the shaded region in this figure. ...
... As the function f(x) = (ln x)/x in the example is positive for x > 1, the integral represents the area of the shaded region in this figure. ...
Area under a Graph
... In class on Wed Nov 12, we basically covered Sec 4.7 of Thomas/Finney, though with an emphasis on area functions. Let f (x) be a function with f (x) ≥ 0 for a ≤ x ≤ b. Let R be the region under the graph y = f (x) and above the interval [a, b] on the x-axis. We want to know Area(R). ...
... In class on Wed Nov 12, we basically covered Sec 4.7 of Thomas/Finney, though with an emphasis on area functions. Let f (x) be a function with f (x) ≥ 0 for a ≤ x ≤ b. Let R be the region under the graph y = f (x) and above the interval [a, b] on the x-axis. We want to know Area(R). ...
+ f
... Thus marginal revenue is equal to marginal cost when 50-x/50=5-x/500 Solving, we get x = 2500 To check that this gives a maximum we compute the second derivatives: R"(x) = -1/50 C"(x) = -1/500 Thus R"(x) < C"(x) for all values of x. Therefore a production level of 2500 units will maximize profits. ...
... Thus marginal revenue is equal to marginal cost when 50-x/50=5-x/500 Solving, we get x = 2500 To check that this gives a maximum we compute the second derivatives: R"(x) = -1/50 C"(x) = -1/500 Thus R"(x) < C"(x) for all values of x. Therefore a production level of 2500 units will maximize profits. ...
ASSIGNMENT 1
... (To be done after studying Blocks 1 and 2.) Course Code : MTE-01 Assignment Code : MTE-01/AST-1/2004 Maximum Marks : 100 ...
... (To be done after studying Blocks 1 and 2.) Course Code : MTE-01 Assignment Code : MTE-01/AST-1/2004 Maximum Marks : 100 ...
Problem Set 3 Partial Solutions
... e + C. For the integral of , write = · and use the scalar linearity property ...
... e + C. For the integral of , write = · and use the scalar linearity property ...
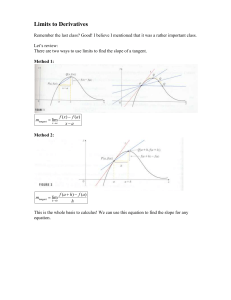
Limits to Derivatives
... derivative. The derivative is a function that represents the slope of a function at any point. We use two main ways to represent a function. The derivative of a function f(x) is f’(x) [we say: “f prime of x” or simply “the derivative of f”]. df (x) dy Another way to represent the derivative of the r ...
... derivative. The derivative is a function that represents the slope of a function at any point. We use two main ways to represent a function. The derivative of a function f(x) is f’(x) [we say: “f prime of x” or simply “the derivative of f”]. df (x) dy Another way to represent the derivative of the r ...
Assignments Derivative Techniques
... 5. a. Find the instantaneous rate of change of the volume of a cube as a function of its edge length x, in cm. b. Find the average rate of change of the volume of a cube on the interval 2 cm x 11 cm. c. For what value of x does the instantaneous rate of change of the volume equal the average rat ...
... 5. a. Find the instantaneous rate of change of the volume of a cube as a function of its edge length x, in cm. b. Find the average rate of change of the volume of a cube on the interval 2 cm x 11 cm. c. For what value of x does the instantaneous rate of change of the volume equal the average rat ...
... y = x3 − 6x2 + x + 3 where the tangents are parallel to the line y = x + 5. If the tangents have to be parallel to the line then they must have the same gradient. The standard equation for a straight line is y = mx + c, where m is the gradient. So what we gain from looking at this standard equation ...
Ch 11.10 Taylor Series
... whose graph is the tangent line (Calculus I §2.9). We can improve this approximation of f (x) in two ways: • Take more terms, increasing N . • Take the center a close to x, giving small (x−a) and tiny (x−a)n . A Taylor series centered at a = 0 is specially named a Maclaurin series. Example: sine fun ...
... whose graph is the tangent line (Calculus I §2.9). We can improve this approximation of f (x) in two ways: • Take more terms, increasing N . • Take the center a close to x, giving small (x−a) and tiny (x−a)n . A Taylor series centered at a = 0 is specially named a Maclaurin series. Example: sine fun ...
Test #2 Review
... How to tell if the limit of f(x,y) as x, y tends to a, b exists and how to find its value. How to find partial derivatives, and second order partial & mixed partial derivatives; and how to use the chain rules. How to find total differentials and how to use them to estimate percentage errors in m ...
... How to tell if the limit of f(x,y) as x, y tends to a, b exists and how to find its value. How to find partial derivatives, and second order partial & mixed partial derivatives; and how to use the chain rules. How to find total differentials and how to use them to estimate percentage errors in m ...
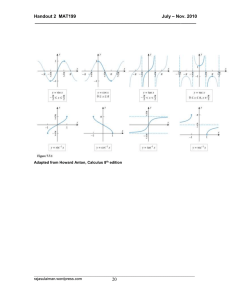
Calculus I Homework: Inverse Functions and Logarithms Page 1
... Example Graph the given functions on a common screen. How are these graphs related? y = log1.5 x, y = ln x, y = log10 x, y = log50 x Example Starting with the graph of y = ln x, find the equation of the graph that results from a) shifting 3 units upward, b) shifting 3 units to the left, c) reflectin ...
... Example Graph the given functions on a common screen. How are these graphs related? y = log1.5 x, y = ln x, y = log10 x, y = log50 x Example Starting with the graph of y = ln x, find the equation of the graph that results from a) shifting 3 units upward, b) shifting 3 units to the left, c) reflectin ...
The Fundamental Theorem of Calculus and Integration
... In the expression above, there is no reason why f (xi ) must always be positive. If a function is always negative, then the Riemann sum will be negative. Thus, we can think of the FTC as saying two different things: • If f (x) ≥ 0, then the integral gives you the area. • If f (x) ≤ 0, then the integ ...
... In the expression above, there is no reason why f (xi ) must always be positive. If a function is always negative, then the Riemann sum will be negative. Thus, we can think of the FTC as saying two different things: • If f (x) ≥ 0, then the integral gives you the area. • If f (x) ≤ 0, then the integ ...
Lecture 9 (Part 1)
... The Logarithm Function loga x is defined as loga x = y if and only if ay = x. a is called the base of the logarithm. In calculus the most useful base for logarithms is the number e The Natural Logarithm Function The natural logarithm function, denoted by ln x, is defined as ln x = y if and only if e ...
... The Logarithm Function loga x is defined as loga x = y if and only if ay = x. a is called the base of the logarithm. In calculus the most useful base for logarithms is the number e The Natural Logarithm Function The natural logarithm function, denoted by ln x, is defined as ln x = y if and only if e ...
solution of diffusion equation with local derivative
... In the most recent century, mathematics apparatus were employed to replicate real world problems, which take place in all branches of sciences. The diffusion equation is a partial differential equation that portrays density dynamics in a material undertakes diffusion. It is also used to describe pro ...
... In the most recent century, mathematics apparatus were employed to replicate real world problems, which take place in all branches of sciences. The diffusion equation is a partial differential equation that portrays density dynamics in a material undertakes diffusion. It is also used to describe pro ...
Continuous functions( (الدوال المستمرة introduction The concept of
... The concept of continuous function is basic to much of mathematics .continuous functions on the real line appear in the first of any calculus book ,and continuous functions in the plane and in a space follow and far behind ,more general kinds of continuous functions arise as one goes further in math ...
... The concept of continuous function is basic to much of mathematics .continuous functions on the real line appear in the first of any calculus book ,and continuous functions in the plane and in a space follow and far behind ,more general kinds of continuous functions arise as one goes further in math ...
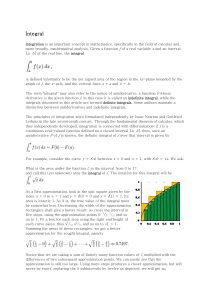
Integral
... is defined informally to be the net signed area of the region in the xy-plane bounded by the graph of ƒ, the x-axis, and the vertical lines x = a and x = b. The term "integral" may also refer to the notion of antiderivative, a function F whose derivative is the given function ƒ. In this case it is c ...
... is defined informally to be the net signed area of the region in the xy-plane bounded by the graph of ƒ, the x-axis, and the vertical lines x = a and x = b. The term "integral" may also refer to the notion of antiderivative, a function F whose derivative is the given function ƒ. In this case it is c ...
randolph township school district
... The limit of a function exists if and only if the limits from both sides of c exist and are equal. lim f ( x) L exists if and only if x ...
... The limit of a function exists if and only if the limits from both sides of c exist and are equal. lim f ( x) L exists if and only if x ...
Rate Of Change Assignment
... 2. For each of the following functions, sketch the function and then state the intervals where: The function is positive/negative The function is increasing/decreasing The slope of the tangent is increasing/decreasing ...
... 2. For each of the following functions, sketch the function and then state the intervals where: The function is positive/negative The function is increasing/decreasing The slope of the tangent is increasing/decreasing ...
Chapter 4 Study Guide (Exam 3)
... ___• Write a complete statement of the Extreme Value Theorem (pg 246). Illustrate the Extreme Value Theorem graphically. Give graphical examples to show that when any of the hypotheses of the Extreme Value Theorem are not satisfied, the function may or may not have an absolute maximum or minimum. St ...
... ___• Write a complete statement of the Extreme Value Theorem (pg 246). Illustrate the Extreme Value Theorem graphically. Give graphical examples to show that when any of the hypotheses of the Extreme Value Theorem are not satisfied, the function may or may not have an absolute maximum or minimum. St ...
1 Distributions or generalized functions.
... v = 0. This is one of the main difference between modules and vector spaces. Proposition 1.3. If L ∈ D0 satisfies x.L = 0 then there exists a constant c such that L = cδ . Proof. Fix ψ ∈ D a function such that ψ(0) = 1. We claim that L − cδ = 0 where c = hL, ψi. Indeed, any test ϕ can be written as ...
... v = 0. This is one of the main difference between modules and vector spaces. Proposition 1.3. If L ∈ D0 satisfies x.L = 0 then there exists a constant c such that L = cδ . Proof. Fix ψ ∈ D a function such that ψ(0) = 1. We claim that L − cδ = 0 where c = hL, ψi. Indeed, any test ϕ can be written as ...
A Collection of Proofs
... takes on every complex value with the possible exception of one complex number. For example, the function f z e z takes on every complex value except for 0. Theorem. 0 1 z PROOF. Applying Picard’s Theorem to the nonconstant, analytic function f z ee , this function takes on all complex ...
... takes on every complex value with the possible exception of one complex number. For example, the function f z e z takes on every complex value except for 0. Theorem. 0 1 z PROOF. Applying Picard’s Theorem to the nonconstant, analytic function f z ee , this function takes on all complex ...
Section 4.2 Class Notes
... *Note that the leading coefficient of the projectile motion model is 4.9 . This constant is derived using calculus and the acceleration of gravity on earth, which is 9.8 meters per second per second. If the height was measured in feet, the leading coefficient of the projectile motion model would be ...
... *Note that the leading coefficient of the projectile motion model is 4.9 . This constant is derived using calculus and the acceleration of gravity on earth, which is 9.8 meters per second per second. If the height was measured in feet, the leading coefficient of the projectile motion model would be ...
AP Calculus AB Course Outline
... the use of color. Students are expected to use proper vocabulary and terminology when giving verbal explanations to their fellow classmates, as well as to the instructor. Technology is also available through the use of a Texas Instruments TI-89 graphing calculator that can be viewed via an overhead ...
... the use of color. Students are expected to use proper vocabulary and terminology when giving verbal explanations to their fellow classmates, as well as to the instructor. Technology is also available through the use of a Texas Instruments TI-89 graphing calculator that can be viewed via an overhead ...