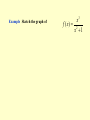Download + f

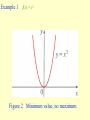
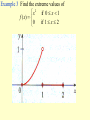
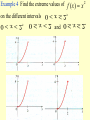
Chapter 3
The mean value theorem and
curve sketching
3.3 MONOTONIC FUNCTIONS AND THE FIRST DERIVATIVE TEST
In sketching the graph of a function it is very useful to know where it rises and
where it falls. The graph shown in Figure1 rises from A to B, falls from B to C,
and rises again from C to D.
Figure 1
(1) DEFINITION A function f is called increasing on an interval I if
f ( x1 )  f ( x2 ) whenever x1  x2 in I .
A function that is increasing or decreasing on I is called monotonic on I.
TEST FOR MONOTONIC FUNCTIONS Suppose f is continuous on [a, b] and differentiable
on
(a,b).
(a) If f'(x) > 0 for all x in (a,b),
then f is increasing on [a, b].
(b) If f'(x) < 0 for all x in (a, b), then f is decreasing on [a, b].
PROOF (a) Let x1 and x2 be any two numbers in [a, b] with x1<x2 . Then f is
continuous on [x1, x2] and differentiable on (x1, x2), so by the Mean Value Theorem
there is a number c between x1 and x2 such that
(2)
Now f '(c) > 0 by assumption and x2 -x1> 0 because x1<x2 . Thus the right side of
Equation 2 is positive, and so
f ( x2 )  f ( x1 )  f (c)( x2  x1 )
This shows that f is increasing on [a,b].
It is similar to prove (b).
f ( x2 )  f ( x1 )  0
or f ( x1 )  f ( x2 ).
Example 1 Find where the function f (x) = 3x4 - 4x3 - 12x2 +5
is increasing and where it is decreasing.
THE FIRST DERIVATIVE TEST Suppose that c is
a critical number of a continuous function f.
(a) If f ' changes from positive to negative at c, then f
has a local maximum at c.
(b) If f ' changes from negative to positive at c then f
has a local minimum at c.
(c) If f ' does not change sign at c (that is f ' is positive
on both sides of c or negative on both sides), then
f has no local extremum at c.
Example 3 Find the local and absolute extreme values of the function f(x)= x3(x -2)2, -1
3. Sketch its graph.
x
f(6/5)=1.20592 is a local maximum; f(2)=0
is a local minimum; absolute maximum
value is f(3)=27; absolute minimum value
is f(-1)=-9. The sketched in Figure 6.
3.4 CONCAVITY AND POINTS OF INFLECTION
Figure 1
Figure 2
(a) Concave upward
(b) Concave downward
(1) DEFINITION If the graph of f lies above all of its tangents on an interval I, then it is
called concave upward on I. If the graph of f lies below all of its tangents on f , it is called
concave downward on I.
Figure 3 shows the graph of a function that is concave
upward (abbreviated CU) on the intervals (b, c), (d, e),
and (e,p) and concave downward (CD) on the intervals
(a, b), (c,d), and (p,q)
THE TEST FOR CONCAVITY Suppose f is twice differentiable on an interval I.
(a) If f "(x) > 0 for all x in I, then the graph of f is concave
upward on I.
(b) If f"(x) < 0 for all x in I, then the graph of f is concave
downward on I.
The equation of this tangent
is y  f (a)  f (a)( x  a)
we must show that
f ( x)  f (a)  f (a)( x  a)
whenever
x  I ( x  a)
(See Figure 4.)
Figure 4
Proof of (a) First let us take the case where x > a. Applying the Mean
Value Theorem to f on the interval [a,.x], we get a number c, with
a < c < x, such that
(2)
f (x) - f(a) == f’ (c) (x - a)
Since f " > 0 on f we know from the Test for Monotonic Functions that f ' is
increasing on I. Thus, since a < c, we have
f'(a)<f’(c)
and so, multiplying this inequality by the positive number x -a ,we get
(3)
Now we add f(a) to both sides of this equality:
f(a) +. f'(a) (x - a) < f(a) + f'(c) (x - a)
But from Equation 2 we have f(x) = f(a) + f'(c) (x -a). So this inequality becomes
(4)
f(x)>f(a) +f '(a)(x-a)
f (a)( x  a)  .f (c)( x  a)
which is what we wanted to prove.
For the case where x < a,we have f'(c) < f'(a), but multiplication by the negative
number x - a reverses the inequality, so we get (3) and (4) as before.
(2) DEFINITION A point P on a curve is called a point of inflection if the
curve changes from concave upward to concave downward or from concave
downward to concave upward at P.
Example 1 Determine where
the curve y=x3 -3x+1 is
concave upward and where it
is concave downward. Find
the inflection points and
sketch the curve.
THE SECOND DERIVATIVE TEST Suppose f " is continuous on an open interval that
contains c.
(a) If f '(c)=0 and f "(c) > 0, then f has a local minimum at c.
(b) If f '(c)=0 and f "(c) < 0, then f has a local maximum at c.
Example 2 Discuss the curve y = x4 - 4x3 with respect to concavity, points of inflection, and
local extrema. Use this information to sketch the curve.
Since f '(3) = 0 and f "(3) >0,f (3)
= -27 is a local minimum. The
point (0,0) is an inflection point
since the curve changes from
concave upward to concave
downward there. Also (2, -16)
since the curve changes from
concave downward to concave
upward there.
3.5
Limits at infinity, horizontal
asymptotes
Figure 1
(1) DEFINITION Let f be a function defined on some interval , Then
lim f ( x)  L
means that the values of f (x) can be made arbitrarily close to L by taking x
sufficiently large.
x 
(2) DEFINITION Let f be a function defined on
some interval
  ( , a), Then
lim f ( x)  L
x 
means that the values of f(x) can be made arbitrarily
close to L by taking x sufficiently large negative.
(3) DEFINITION The line y = L is called a horizontal asymptote of the
curve
y
=
f(x)
if
either
lim
f
(x)
=
L
or
lim
f
(x)
=
L
x 
x  
(4) THEOREM If r >0 is a rational number, then
1
lim that
is0defined for all x, then
If r > 0 is a rational number such
r
x  x
1
lim r  0
x   x
Infinite limits at infinity
The notation
lim f ( x)  
x 
is used to indicate that the values of f(x) become large as x
becomes large.Similar meanings are attached to the following
symbols:
lim f ( x)  
x  
lim f ( x)   lim f ( x)  
x 
x  
Example 1
Example 2
(5) DEFINITION Let f be a function defined on some
interval
. Then
( a,  )
means that for every
N such that
therefis( axcorresponding
number
lim
)L
x 
whenever
x > N.
 0
f ( x)  L  
(6) DEFINITION Let f be a function defined on some
interval
. Then
(, a )
means that for every
such that
lim f ( x)  L
there is a corresponding number N
x 
whenever x < N.
 0
f ( x)  L  
(7) DEFINITION
(a, )Let f be a function defined on some interval
. Then
lim
f
(
x
)


means that for every positive M there is a corresponding number N such that
x 
whenever x > N.
f ( x)  M
3.6
Curve sketching
(1) This section is to discuss how to
sketch the graph of a curve. In high
school we learnt to plot points and join
the points in order.
Example
2
y=x
(2) In this section we will draw the graph by
following
steps:
A. Domain The first step is to determine the domai
of the function f.
B. Intercept Find the x- and y-intersepts .
C. Symmetry (i) even
(ii) odd
(iii) periodic
D. Asymptotes: (i) Horizontal asymptotes
(ii)Vertical asymptotes
(iii)slant asymptotes
E. Intervals of increase or decrease Use the test for
monotonic functions.
F. Local maximum and minimum valuves Find the
critical numbers of f.
G. Concavity and points of inflection Compute f"(x)
and use the test for concavity.
H. Sketch the curve Using the information in
A---G , draw the graph.
Example Discuss the curve
2
2x
y 2
x 1
Solution
A.Domain
B. Intercept
C. Symmetry
D. Asymptotes E. Intervals of increase or decrease
F. Local maximum and minimum values
G. Concavity and points of inflection
H. Sketch the curve
Slant asymptotes
Some curves have asymptotes that are
oblique, that is, neither horizontal nor
vertical.
lim [ f ( x)  (mx  b)]  0
x 
If
, then the line
y=mx+b is called a slant asymptotes,
because the vertical distance between the
curve y=f(x) and the line y=mx+b
approaches 0.
3
Example Sketch the graph of
x
f ( x)  2
x 1
3.9 Applications to Economics
Cost function C (x )
Average function
If the average cost is a minimum, then marginal cost =
average cost
Example 1 A company estimates that the cost (in
dollars) of producing x items is
(a) Find the cost, average cost, and marginal cost of
producing 1000 items, 2000 items, and 3000 items.
(b) At what production level will the average cost be lowest,
and what is this minimum average cost?
Solution
(a) The average cost function is
C ( x) 2600
c
(
x
)



2

0
.
001
x
The marginal cost function
x is x
C'(x) = 2 + 0.002x
(b) To minimize the average cost we must have marginal cost = average cost C'(x)
= c(x)
2 + 0.002x = 2600/x+ 2 + 0.001x
This equation simplifies to
0.001x = 2600/x
so x2 =2600/0.001 = 2,600,000
and
To see that this production level actually gives a minimum we note that
c"(x) =5200/x3> 0, so c is concave upward on its entire domain. The minimum
average cost is
x  2,600,000  1612
c(1612) = 2600/1612+2+0.001(1612) = $5.22/item
Let p(x) be the price per unit that the company can charge if it sells x
units. Then p is called the demand function (or price function) and
we would expect it to be a decreasing function of x. If x units are sold
and the price per unit is p(x), then the total revenue is
R(x) = x p(x)
and R is called the revenue function (or sales function). The
derivative R' of the revenue function is called the marginal revenue
function and is the rate of change of revenue with respect to the
number of units sold.
If x units are sold, then the total profit is
P(x) = R(x) - C(x)
and P is called the profit function. The marginal profit function is P', the
derivative of the profit function. In order to maximize profit we look for the
critical numbers of P, that is, the numbers where the marginal profit is 0. But if
P'(x) = R'(x) - C'(x) = 0
then
R'(x) = C'(x)
Therefore
If the profit is a maximum, then
marginal revenue = marginal
cost
To ensure that this condition gives a maximum we could use the
Second Derivative Test. Note that
P"(x) = R"(x) - C"(x) < 0
when
R"(x) < C"(x)
and this condition says that the rate of increase of marginal revenue is
less than the rate of increase of marginal cost. Thus the profit will be a
maximum when
R'(x) = C'(x) and R"(x) < C"(x)
Example 2 Determine the production level that will maximize the profit for a
company with cost and demand functions
C(x) = 3800 + 5x - x2/1000 p(x) = 50 - x/100
SOLUTION The revenue function is R(x) = x p(x) = 50x -x2/100
so the marginal revenue function is R'(x) = 50 -x/50
and the marginal cost function is C'(x)=5-x/500
Thus marginal revenue is equal to marginal cost when
50-x/50=5-x/500
Solving, we get
x = 2500
To check that this gives a maximum we compute the second derivatives:
R"(x) = -1/50 C"(x) = -1/500
Thus R"(x) < C"(x) for all values of x. Therefore a production level of 2500 units will
maximize profits.
3.10 Antiderivatives
We know how to solve the derivative problem: given a function, find its
derivative. But many problems in mathematics and its applications require us
to solve the inverse of the derivative problem: given a function, find a function
F whose derivative is f. If such a function F exists, it is called an antiderivative
of f.
(1) DEFINITION A function F is called an
antiderivative of f on an interval I if F '(x) = f (x)
for all x in I.
(2) THEOREM If F is an antiderivative of f on an interval I, then the most
general antiderivative of f on I is
F(x) + C
where C is an arbitrary constant.
(3) Table of antidifferntiation formulas
Some of the most important applications of differential
calculus are optimization problems, in which we are
required to find the optimal (best) way of doing something.
In many cases these problems can be reduced to finding the
maximum or minimum values of a function. Let us first
explain exactly what we mean by maximum and minimum
values.
3.1 MAXIMUM AND MINIMUM
VALUES
Figure 1
Minimum value f(a)
Maximum value f(d)
In Figure 1, if we consider only values of x near b [for instance,
if we restrict our attention to the interval (a,c)], then f(b) is the
largest of those values of f(x) and is called a local maximum
value of f. Likewise, f(c) is called a local minimum value of f
because f(c)  f(x) for x near c [in the interval (b, d), for instance].
The function f also has a local minimum at e. In general we
have the following definition.
Example 1 f(x) = x2
Figure 2 Minimum value, no maximum
Example 2
Please find the absolute maximum, the absolute
minimum, local maximum and local minimum of the function
f ( x)  3x  16 x  18x
4
3
2
1  x  4
We have seen that some functions have extreme values,
while others do not. The following theorem gives conditions
under which a function is guaranteed to possess extreme values.
(3) THE EXTREME VALUE THEOREM If f is continuous
on a closed interval [a,b], then f attains an absolute
maximum value f(c) and an absolute minimum value f(d) at
some numbers c and d in [a, b].
The extreme value theorem is illustrated in the
following.
Figure 5
Example 3 Find the extreme values of
2
x
if 0  x  1
f ( x)  
if 1  x  2
0
Example 4 Find the extreme values of f ( x)  x 2
0

x

2
,
on the different intervals
0  x  2, 0  x  2 and 0  x  2.
(4) FERMAT' S THEOREM If f has a local extremum
(that is, maximum or minimum) at c, and if f '(c) exists, then
f '(c) =0.
(5) DEFINITION A critical number of a function f is a
number c in the domain of f such that either f '(c) = 0 or f '(c)
does not exist.
(6) If f has a local extremum at c, then c is a critical number
of f .
(7) To find the absolute maximum and minimum values
of a continuous function f on a closed interval [a, b]:
1. Find the values of f at the critical numbers of f in (a, b).
2. Find the values of f(a) and f(b).
3. The largest of the values from steps 1 and 2 is the absolute
maximum value; the smallest of these values is the absolute
minimum value.
Example 5 Find the absolute maximum and minimum values of the
function
1
3
2
f ( x)  x  3 x  1   x  4
2
3.2 THE MEAN VALUE THEOREM
We will see that many of the results of this chapter depend
on one central fact, which is called the Mean Value
Theorem. But to arrive at the Mean Value Theorem we first
need the following result.
ROLLE'S THEOREM Let f be a function that satisfies the
following three hypotheses:
1. f is continuous on the closed interval [a, b].
2. f is differentiable on the open interval (a,b).
3. f(a)=f(b)
Then there is a number c in (a,b) such that f '(c) = 0.
Figure 1
PROOF There are three cases:
CASE I f(x) = k, a constant. Then f '(x) = 0, so the number c can be
taken any number in (a,b).
CASE II f(x)> f(a) for some x in (a, b) [as in Figure l(b) or (c)]
By the Extreme Value Theorem (which we can apply by hypothesis
1) f has a maximum value somewhere in [a, b]. Since f (a) = f (b), it
must attain this maximum value at a number c in the open interval (a,
b). Then f has a local maximum at c and, by hypothesis 2, f is
differentiable at c. Therefore f '(c) = 0 by Fermat's Theorem.
CASE lll f(x) < f(a) for some x in (a,b) [as in Figure l (c) or (d)]
By the Extreme Value Theorem, f has a minimum value in [a, b]
and, since f(a) = f(b), it attains this minimum value at a number c
in (a,b). Again f '(c) = 0 by Fermat's Theorem.
Example 1 Prove that the equation x3 + x -1 = 0 has exactly one real
root.
SOLUTION First we use the
Intermediate Value Theorem
(1,5.9) to show that a root
exists.
To show that the equation has
no other real root we use
Rolle's Theorem and argue by
contradiction.
THE MEAN VALUE THEOREM
Let f be a function that satisfies the following hypotheses:
1. f is continuous on the closed interval [a, b].
2. f is differentiable on the open interval (a, b).
Then there is a number c in (a,b) such that
(1)
f (b)  f (a)
f (c) 
ba
or, equivalently,
(2)
f (b)  f (a)  f (c)(b  a)
we can see that it is reasonable by interpreting it geometrically.
The slope of the secant line AB is
f (b)  f (a)
mab 
ba
PROOF The equation of the line AB can be written as
f (b)  f (a)
f (b)  f (a)
y  f (a) 
( x  a) or as y  f (a) 
( x  a)
ba
ba
Figure 5
f (b)  f (a)
(3) h( x)  f ( x)  f (a) 
( x  a)
ba
First we must verify that h satisfies the three hypotheses of
Rolle's Theorem
1. The function h is continuous on [a, b] because it is the sum
of f and a first-degree polynomial, both are continuous.
2. The function h is differentiable on (a, b) because both f and
the first-degree polynomial are differentiable. In fact, we can
f (b)  f (a)
compute h' directly from Equation 4: 
h ( x)  f ( x) 
ba
3. h(a) =h(b).
f (b)  f (a)
0  h(c)  f (c) 
ba
Since h satisfies the hypotheses of Rolle's Theorem, that theorem
says there is a number c in (a, b) such that h’ (c) =0. Therefore
and so
f (b)  f (a )
f (c) 
ba
Example 2 To illustrate the Mean Value Theorem with a specific
function, let us consider f (x) = x3 - x , a = 0, b = 2.
Figure 6 illustrates this
calculation: the tangent line
at this value of c is parallel
to the secant line OB.
Figure 6
The Mean Value Theorem can be used to establish some of the basic
facts of differential calculus. One of these basic facts is the following
theorem.
(3) THEOREM If f ' (x) = 0 for all x in an interval (a, b),
then f is constant on (a, b)
(4) COROLLARY If f '(x) = g'(x) for all x in an interval (a, b),
then f - g is constant on (a,b); that is , f (x) = g(x) + c where c
is a constant.