Microsoft Word Viewer
... Piecewise functions are defined in “pieces” because the function behaves differently on some intervals from the way it behaves on others. The individual pieces of the function may be linear, polynomial, rational or a combination of these. The parts of the domain are usually specified in the form of ...
... Piecewise functions are defined in “pieces” because the function behaves differently on some intervals from the way it behaves on others. The individual pieces of the function may be linear, polynomial, rational or a combination of these. The parts of the domain are usually specified in the form of ...
MA123, Chapter 2: Change, and the idea of the derivative (pp. 17
... tangent line to the graph of a function f at a point P (x1 , f (x1 )) lies in the fact that if we look at a portion of the graph of f near the point P , it becomes indistinguishable from the tangent line at P . In other words, the values of the function are close to those of the linear function whos ...
... tangent line to the graph of a function f at a point P (x1 , f (x1 )) lies in the fact that if we look at a portion of the graph of f near the point P , it becomes indistinguishable from the tangent line at P . In other words, the values of the function are close to those of the linear function whos ...
Department of Physics and Mathematics
... studying properties and graphs of functions, limits, derivatives, max/min theory, integrals, the definite integral, Mean Value Theorems, the Fundamental Theorem of Calculus, and their applications and derivatives and integrals of transcendental functions TEXT and COVERAGE: Swokowski, Calculus, The C ...
... studying properties and graphs of functions, limits, derivatives, max/min theory, integrals, the definite integral, Mean Value Theorems, the Fundamental Theorem of Calculus, and their applications and derivatives and integrals of transcendental functions TEXT and COVERAGE: Swokowski, Calculus, The C ...
natural logarithmic function.
... It is likely that you have studied logarithms in an algebra course. There, without the benefit of calculus, logarithms would have been defined in terms of a base number. For example, common logarithms have a base of 10 and therefore log1010 = 1. The base for the natural logarithm is defined using th ...
... It is likely that you have studied logarithms in an algebra course. There, without the benefit of calculus, logarithms would have been defined in terms of a base number. For example, common logarithms have a base of 10 and therefore log1010 = 1. The base for the natural logarithm is defined using th ...
Calculus Curriculum Questionnaire for Greece
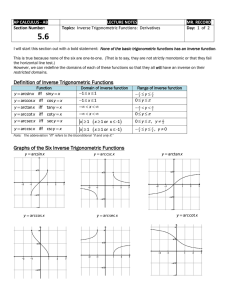
... functions Limits of trigonometric functions Continuity of trigonometric functions Derivatives of trigonometric functions Graphs of trigonometric functions Definition of inverse trigonometric functions Limits of inverse trigonometric functions Continuity of inverse trigonometric functions Derivative ...
... functions Limits of trigonometric functions Continuity of trigonometric functions Derivatives of trigonometric functions Graphs of trigonometric functions Definition of inverse trigonometric functions Limits of inverse trigonometric functions Continuity of inverse trigonometric functions Derivative ...
natural logarithmic function.
... It is likely that you have studied logarithms in an algebra course. There, without the benefit of calculus, logarithms would have been defined in terms of a base number. For example, common logarithms have a base of 10 and therefore log1010 = 1. The base for the natural logarithm is defined using th ...
... It is likely that you have studied logarithms in an algebra course. There, without the benefit of calculus, logarithms would have been defined in terms of a base number. For example, common logarithms have a base of 10 and therefore log1010 = 1. The base for the natural logarithm is defined using th ...
Locating a Railway Supply Depot
... assumptions in setting up the model, and so there are several questions about the model that we should consider. For example, is the model a realistic one? The model depends on the distance from x to each xi , and also on the number Ni of trips from the parts center to xi . How can we determine Ni ? ...
... assumptions in setting up the model, and so there are several questions about the model that we should consider. For example, is the model a realistic one? The model depends on the distance from x to each xi , and also on the number Ni of trips from the parts center to xi . How can we determine Ni ? ...
AP Calculus AB Course Syllabus 2016-2017
... writing assignments. This notebook, along with a pen/pencil will be brought to every class. 2. If you are absent, it is your responsibility to check with the teacher and complete any missed assignments. 3. Homework will be checked. Incomplete homework is no homework. An incomplete homework will resu ...
... writing assignments. This notebook, along with a pen/pencil will be brought to every class. 2. If you are absent, it is your responsibility to check with the teacher and complete any missed assignments. 3. Homework will be checked. Incomplete homework is no homework. An incomplete homework will resu ...
Page 1 MCV4U0 PROBLEM SET V: Derivatives II In order to receive
... Let the base of the rectangle be u and let the height of the rectangle be y. Clearly from the diagram, the base of the rectangle can be written in terms of x as well as the height y can be written in x. From the diagram provided, x + u = 4 which implies that u = 4 − x . Furthermore, y lies on the cu ...
... Let the base of the rectangle be u and let the height of the rectangle be y. Clearly from the diagram, the base of the rectangle can be written in terms of x as well as the height y can be written in x. From the diagram provided, x + u = 4 which implies that u = 4 − x . Furthermore, y lies on the cu ...
First Order Predicate Logic
... • This lecture looked at predicate (or first order) logic. • Predicate logic is a generalization of propositional logic. • The generalization requires the use of quantifiers, and these need special rules for handling them when doing inference. • We looked at how the proof rules for propositional log ...
... • This lecture looked at predicate (or first order) logic. • Predicate logic is a generalization of propositional logic. • The generalization requires the use of quantifiers, and these need special rules for handling them when doing inference. • We looked at how the proof rules for propositional log ...
Expected Values of Random Variables
... Outline: Expectation of a Geometric RV: Let X ~ GEOM(p). We want to show (analytically) that E(X) = 1/p. Already demonstrated in R for p = 1/2. Consider the random variables gt(X) = etX. By summing a geometric series we can show that mX(t) = E(etX) = pet/(1 – qet), for t in a neighborhood of t = 0. ...
... Outline: Expectation of a Geometric RV: Let X ~ GEOM(p). We want to show (analytically) that E(X) = 1/p. Already demonstrated in R for p = 1/2. Consider the random variables gt(X) = etX. By summing a geometric series we can show that mX(t) = E(etX) = pet/(1 – qet), for t in a neighborhood of t = 0. ...
Section 2.6 Special Functions
... F.IF.4 For a function that models a relationship between two quantities, interpret key features of graphs and tables in terms of the quantities, and sketch graphs showing key features given a verbal description of the relationship. F.IF.7.b Graph square root, cube root, and piecewise-defined functio ...
... F.IF.4 For a function that models a relationship between two quantities, interpret key features of graphs and tables in terms of the quantities, and sketch graphs showing key features given a verbal description of the relationship. F.IF.7.b Graph square root, cube root, and piecewise-defined functio ...
5.6: Inverse Trigonometric Functions: Differentiation
... I will start this section out with a bold statement: None of the basic trigonometric functions has an inverse function. This is true because none of the six are one-to-one. (That is to say, they are not strictly monotonic or that they fail the horizontal line test.) However, we can redefine the doma ...
... I will start this section out with a bold statement: None of the basic trigonometric functions has an inverse function. This is true because none of the six are one-to-one. (That is to say, they are not strictly monotonic or that they fail the horizontal line test.) However, we can redefine the doma ...
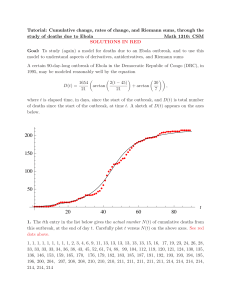
20 40 60 80 t 50 100 150 200
... interval. Then total change in D(t) over the interval = rate of change R over the interval ⇥ length of interval (for example: if your speed is a constant 60 mph for an interval of length 1 sec = 1/3600 of an hour, then your total distance traveled over that second is 60 ⇥ 1/3600 = 1/60 of a mile (=8 ...
... interval. Then total change in D(t) over the interval = rate of change R over the interval ⇥ length of interval (for example: if your speed is a constant 60 mph for an interval of length 1 sec = 1/3600 of an hour, then your total distance traveled over that second is 60 ⇥ 1/3600 = 1/60 of a mile (=8 ...
Slide 1
... The function f ( x) x n x is a root function. For n = 2, it is the square root function f ( x) x , whose domain is [0, ) and whose graph is the upper half of the parabola x = y2. For other even values of n, the graph of y n x is similar to that of y x . ...
... The function f ( x) x n x is a root function. For n = 2, it is the square root function f ( x) x , whose domain is [0, ) and whose graph is the upper half of the parabola x = y2. For other even values of n, the graph of y n x is similar to that of y x . ...
The Dirac Delta Function - Rose
... One of the most useful applications of delta functions and impulse responses is for system or parameter identification. Suppose you have some physical system which is modelled by an ODE, but the model contains certain unknown physical parameters. For example, you may have a spring-mass system govern ...
... One of the most useful applications of delta functions and impulse responses is for system or parameter identification. Suppose you have some physical system which is modelled by an ODE, but the model contains certain unknown physical parameters. For example, you may have a spring-mass system govern ...
The American Statistician The Mean Value Theorem and Taylor`s
... where ∇f (θ ) (a row vector) is the gradient of f at θ . However, the MVT for vector-valued differentiable functions does not exist. To see this, consider a vector-valued function f . For an open convex subset G ⊂ Rp (p ≥ 1), the function f : G → Rq (q > 1) is said to be differentiable at x ∈ G if t ...
... where ∇f (θ ) (a row vector) is the gradient of f at θ . However, the MVT for vector-valued differentiable functions does not exist. To see this, consider a vector-valued function f . For an open convex subset G ⊂ Rp (p ≥ 1), the function f : G → Rq (q > 1) is said to be differentiable at x ∈ G if t ...
CALCULUS 3: NOTES AND EXERCISES ON CRAMER'S RULE
... by the column of entries at the right side of the system of equations. However, there are much more efficient ways of solving such a system when n > 3, so Cramer’s rule is rarely used in this case. ...
... by the column of entries at the right side of the system of equations. However, there are much more efficient ways of solving such a system when n > 3, so Cramer’s rule is rarely used in this case. ...
Solutions to assignment 9 File
... (a) the formulae for differentiating sums, products, sines and cosines; (b) the fact that an everywhere differentiable function whose derivative is zero is constant; (c) the values of cos(0) and sin(0). 6 (From the summer exam 2016) Let F : C → C be a function. A complex number w is said to be a fix ...
... (a) the formulae for differentiating sums, products, sines and cosines; (b) the fact that an everywhere differentiable function whose derivative is zero is constant; (c) the values of cos(0) and sin(0). 6 (From the summer exam 2016) Let F : C → C be a function. A complex number w is said to be a fix ...
UNIVERSAL FUNCTIONS - Muskingum University
... function that can be used to describe all other functions. The Universal Function we will construct in this presentation will be a function whose translations (shift in their graph) will approximate any continuous function we can think of on a given closed bounded interval (i.e. U(x+t)f(x)). Think ...
... function that can be used to describe all other functions. The Universal Function we will construct in this presentation will be a function whose translations (shift in their graph) will approximate any continuous function we can think of on a given closed bounded interval (i.e. U(x+t)f(x)). Think ...
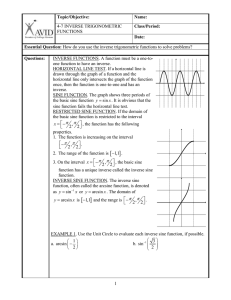
Section 4.7
... 2. If 1 x 1 and 0 y , then cos arccos x x and arccos cos y y ...
... 2. If 1 x 1 and 0 y , then cos arccos x x and arccos cos y y ...