Antiderivatives - John Abbott College
... In a derivative problem, a function f (x) is given and you find the derivative f ′ (x) using the formulas and rules of derivatives shown in a previous tutorial. In an antiderivative problem, the derivative f ′ (x) is given and you find a function f (x) using the formulas of antiderivatives shown lat ...
... In a derivative problem, a function f (x) is given and you find the derivative f ′ (x) using the formulas and rules of derivatives shown in a previous tutorial. In an antiderivative problem, the derivative f ′ (x) is given and you find a function f (x) using the formulas of antiderivatives shown lat ...
AP Calculus
... The “average” slope is the slope of a line drawn from endpoint to endpoint. No matter how much the function may change between endpoints, we say that its “average” change is simply the ratio of changes in y to changes in x. For average slope, use the slope formula. The MVT says that there has to be ...
... The “average” slope is the slope of a line drawn from endpoint to endpoint. No matter how much the function may change between endpoints, we say that its “average” change is simply the ratio of changes in y to changes in x. For average slope, use the slope formula. The MVT says that there has to be ...
The Lambda Calculus - Computer Science, Columbia University
... Function application is written as juxtaposition: f x Every function has exactly one argument. Multiple-argument functions, e.g., +, are represented by currying, named after Haskell Brooks Curry (1900–1982). So, (+ x) is the function that adds x to its argument. Function application associates left- ...
... Function application is written as juxtaposition: f x Every function has exactly one argument. Multiple-argument functions, e.g., +, are represented by currying, named after Haskell Brooks Curry (1900–1982). So, (+ x) is the function that adds x to its argument. Function application associates left- ...
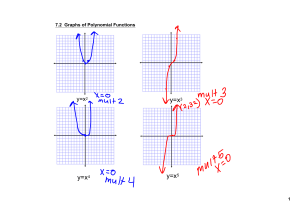
y=x3 y=x4 y=x5
... A polynomial will have a zero that is a real number at each point at which is crosses the x axis. This means that we can graph by finding the ______________ of the function. ...
... A polynomial will have a zero that is a real number at each point at which is crosses the x axis. This means that we can graph by finding the ______________ of the function. ...
BC Ch 4 Assignment Sheet 16-17
... Use pattern recognition to find an indefinite integral. Use a change of variables to find an indefinite integral. Use the General Power Rule for Integration to find an indefinite integral. Use a change of variables to evaluate a definite integral. Evaluate a definite integral involving an even or od ...
... Use pattern recognition to find an indefinite integral. Use a change of variables to find an indefinite integral. Use the General Power Rule for Integration to find an indefinite integral. Use a change of variables to evaluate a definite integral. Evaluate a definite integral involving an even or od ...
Document
... plays no role in the end result So you can change the variable of the integration whenever you feel it convenient ...
... plays no role in the end result So you can change the variable of the integration whenever you feel it convenient ...
INTRODUCTION TO POLYNOMIAL CALCULUS 1. Straight Lines
... We know about the slope of a straight line. It is the change in the y-coordinate divided by the change in the x-coordinate (rise divided by run) as we move from a given point on the line to any other point on the line. The law of similar triangles says that this ratio is independent of the two point ...
... We know about the slope of a straight line. It is the change in the y-coordinate divided by the change in the x-coordinate (rise divided by run) as we move from a given point on the line to any other point on the line. The law of similar triangles says that this ratio is independent of the two point ...
The Analytic Continuation of the Ackermann Function
... • Suggests time could behave as if it is continuous regardless of whether the underlying physics is discrete or continuous. • Continuous iteration connects the “old” and the “new” kinds of science. Partial differential iterated equations • Tetration displays “sum of all paths” behavior, so logical s ...
... • Suggests time could behave as if it is continuous regardless of whether the underlying physics is discrete or continuous. • Continuous iteration connects the “old” and the “new” kinds of science. Partial differential iterated equations • Tetration displays “sum of all paths” behavior, so logical s ...
Honors Precalculus Topics
... Vectors in the plane Unit vectors Operations with vectors Real life applications with vectors Vectors and dot products Vectors in 3 dimensions Use of the cross product Using Triple Scalar Product to find volume of parallelepiped Parametric equations of lines & planes in space Distance between a poin ...
... Vectors in the plane Unit vectors Operations with vectors Real life applications with vectors Vectors and dot products Vectors in 3 dimensions Use of the cross product Using Triple Scalar Product to find volume of parallelepiped Parametric equations of lines & planes in space Distance between a poin ...
Math 1131Q Grading Rubric Fall 2010 Here is the grading rubric for
... 8. (8 pts) An inverted conical tank (i.e., point-down, like an ice cream cone) is 10 feet high and has a diameter of 12 feet at its top. The tank is filled with water at a rate of 4 cubic feet per second. At what rate is the height of the water changing when the water is 7 feet deep? ...
... 8. (8 pts) An inverted conical tank (i.e., point-down, like an ice cream cone) is 10 feet high and has a diameter of 12 feet at its top. The tank is filled with water at a rate of 4 cubic feet per second. At what rate is the height of the water changing when the water is 7 feet deep? ...
MTH/STA 561 GAMMA DISTRIBUTION, CHI SQUARE
... Proof Let y = t (or t = y= ). Then dy = dt (or dt = dy= ). Also, y ! 1 as t ! 1 and y ! 0 as t ! 0. Thus, ...
... Proof Let y = t (or t = y= ). Then dy = dt (or dt = dy= ). Also, y ! 1 as t ! 1 and y ! 0 as t ! 0. Thus, ...
B671-672 Supplemental Notes 2 Hypergeometric, Binomial
... In the study of probablity and its applications to statistics we need to have a collection of random variables (measurable functions) large enough to ensure that probabilities are well defined. Recall that most of classical analysis (calculus, etc.) deals with continuous functions and limits of sequ ...
... In the study of probablity and its applications to statistics we need to have a collection of random variables (measurable functions) large enough to ensure that probabilities are well defined. Recall that most of classical analysis (calculus, etc.) deals with continuous functions and limits of sequ ...
Homework 6 - Select Problems
... y 0 = cos x · cos x + sin x(− sin x) = cos2 (x) − sin2 (x) = cos (2x) By an identity. ...
... y 0 = cos x · cos x + sin x(− sin x) = cos2 (x) − sin2 (x) = cos (2x) By an identity. ...
The Lambda Calculus - Computer Science, Columbia University
... Function application is written as juxtaposition: f x Every function has exactly one argument. Multiple-argument functions, e.g., +, are represented by currying, named after Haskell Brooks Curry (1900–1982). So, (+ x) is the function that adds x to its argument. Function application associates left- ...
... Function application is written as juxtaposition: f x Every function has exactly one argument. Multiple-argument functions, e.g., +, are represented by currying, named after Haskell Brooks Curry (1900–1982). So, (+ x) is the function that adds x to its argument. Function application associates left- ...
Lecture 7: Recall f(x) = sgn(x) = f(x) = { 1 x > 0 −1 x 0 } Q: Does limx
... Theorem 8 (Max-Min Theorem): Let f be continuous on a closed finite interval [a, b]. Then f has an absolute maximum and an absolute minimum on [a, b]. That is, there exist p, q ∈ [a, b] s.t. for all x ∈ [a, b], we have f (p) ≤ f (x) ≤ f (q). Max-Min theorem is (may be) false on open intervals (a, b) ...
... Theorem 8 (Max-Min Theorem): Let f be continuous on a closed finite interval [a, b]. Then f has an absolute maximum and an absolute minimum on [a, b]. That is, there exist p, q ∈ [a, b] s.t. for all x ∈ [a, b], we have f (p) ≤ f (x) ≤ f (q). Max-Min theorem is (may be) false on open intervals (a, b) ...
Riemann Sums Workshop Handout
... The sum on the right hand side is the expanded form. (The contains all the terms I was too lazy to write.) The letter below the sigma is the variable with respect to the sum. All other letters are constants with respect to the sum. ...
... The sum on the right hand side is the expanded form. (The contains all the terms I was too lazy to write.) The letter below the sigma is the variable with respect to the sum. All other letters are constants with respect to the sum. ...
C. CONTINUITY AND DISCONTINUITY
... In a removable discontinuity, lim f (x) exists, but lim f (x) 6= f (a). This may be because x→a ...
... In a removable discontinuity, lim f (x) exists, but lim f (x) 6= f (a). This may be because x→a ...
Lecture 8 - KSU Web Home
... • Of course, the minterm function that we derived from our Kmap was not in simplest terms. • We can, however, reduce our complicated expression to its simplest terms by finding adjacent 1s in the Kmap that can be collected into groups that are powers of two. ...
... • Of course, the minterm function that we derived from our Kmap was not in simplest terms. • We can, however, reduce our complicated expression to its simplest terms by finding adjacent 1s in the Kmap that can be collected into groups that are powers of two. ...