* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Lecture notes
Survey
Document related concepts
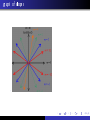
Transcript
Methods of Calculus Summer-2012 Lecture Notes: 1 Exponents Basic Denitions For any real number base x , we dene powers of x : x 0 = 1, x1 = x, x 2 = x .x , x 3 = x .x .x , etc. (The exception is 00 , which is considered indeterminate) Powers are also called exponents. Exponents Basic Denitions For any real number base x , we dene powers of x : x 0 = 1, x1 = x, x 2 = x .x , x 3 = x .x .x , etc. (The exception is 00 , which is considered indeterminate) Powers are also called exponents. Exponents Basic Denitions For any real number base x , we dene powers of x : x 0 = 1, x1 = x, x 2 = x .x , x 3 = x .x .x , etc. (The exception is 00 , which is considered indeterminate) Powers are also called exponents. Exponents Basic Denitions For any real number base x , we dene powers of x : x 0 = 1, x1 = x, x 2 = x .x , x 3 = x .x .x , etc. (The exception is 00 , which is considered indeterminate) Powers are also called exponents. Exponents Basic Denitions For any real number base x , we dene powers of x : x 0 = 1, x1 = x, x 2 = x .x , x 3 = x .x .x , etc. (The exception is 00 , which is considered indeterminate) Powers are also called exponents. Exponents Basic Denitions For any real number base x , we dene powers of x : x 0 = 1, x1 = x, x 2 = x .x , x 3 = x .x .x , etc. (The exception is 00 , which is considered indeterminate) Powers are also called exponents. Cont Examples 20 = 1, 23 = (2)(2)(2) = 8 (=3)4 = (=3) × (=3) × (=3) × (=3) = 81.Also, we can dene√fractional exponents in terms of roots, such as x 21 = x , the square root of x. √ √ 1 3 Similarly, x 3 = 3 x , the cube root of x , x 5 = 5 x 3 , etc. √ m In general, we have x n = n x m , i.e., the nth root of x, raised to the mth power. √ 1 (81) 2 = 81 = 9 , etc. Finally, we can dene negative exponents: x −n = x1n . Thus, x −1 = x1 , etc. Cont Examples 20 = 1, 23 = (2)(2)(2) = 8 (=3)4 = (=3) × (=3) × (=3) × (=3) = 81.Also, we can dene√fractional exponents in terms of roots, such as x 21 = x , the square root of x. √ √ 1 3 Similarly, x 3 = 3 x , the cube root of x , x 5 = 5 x 3 , etc. √ m In general, we have x n = n x m , i.e., the nth root of x, raised to the mth power. √ 1 (81) 2 = 81 = 9 , etc. Finally, we can dene negative exponents: x −n = x1n . Thus, x −1 = x1 , etc. Cont Examples 20 = 1, 23 = (2)(2)(2) = 8 (=3)4 = (=3) × (=3) × (=3) × (=3) = 81.Also, we can dene√fractional exponents in terms of roots, such as x 21 = x , the square root of x. √ √ 1 3 Similarly, x 3 = 3 x , the cube root of x , x 5 = 5 x 3 , etc. √ m In general, we have x n = n x m , i.e., the nth root of x, raised to the mth power. √ 1 (81) 2 = 81 = 9 , etc. Finally, we can dene negative exponents: x −n = x1n . Thus, x −1 = x1 , etc. Cont Examples 20 = 1, 23 = (2)(2)(2) = 8 (=3)4 = (=3) × (=3) × (=3) × (=3) = 81.Also, we can dene√fractional exponents in terms of roots, such as x 21 = x , the square root of x. √ √ 1 3 Similarly, x 3 = 3 x , the cube root of x , x 5 = 5 x 3 , etc. √ m In general, we have x n = n x m , i.e., the nth root of x, raised to the mth power. √ 1 (81) 2 = 81 = 9 , etc. Finally, we can dene negative exponents: x −n = x1n . Thus, x −1 = x1 , etc. Cont Examples 20 = 1, 23 = (2)(2)(2) = 8 (=3)4 = (=3) × (=3) × (=3) × (=3) = 81.Also, we can dene√fractional exponents in terms of roots, such as x 21 = x , the square root of x. √ √ 1 3 Similarly, x 3 = 3 x , the cube root of x , x 5 = 5 x 3 , etc. √ m In general, we have x n = n x m , i.e., the nth root of x, raised to the mth power. √ 1 (81) 2 = 81 = 9 , etc. Finally, we can dene negative exponents: x −n = x1n . Thus, x −1 = x1 , etc. Cont Examples 20 = 1, 23 = (2)(2)(2) = 8 (=3)4 = (=3) × (=3) × (=3) × (=3) = 81.Also, we can dene√fractional exponents in terms of roots, such as x 21 = x , the square root of x. √ √ 1 3 Similarly, x 3 = 3 x , the cube root of x , x 5 = 5 x 3 , etc. √ m In general, we have x n = n x m , i.e., the nth root of x, raised to the mth power. √ 1 (81) 2 = 81 = 9 , etc. Finally, we can dene negative exponents: x −n = x1n . Thus, x −1 = x1 , etc. Cont Examples 20 = 1, 23 = (2)(2)(2) = 8 (=3)4 = (=3) × (=3) × (=3) × (=3) = 81.Also, we can dene√fractional exponents in terms of roots, such as x 21 = x , the square root of x. √ √ 1 3 Similarly, x 3 = 3 x , the cube root of x , x 5 = 5 x 3 , etc. √ m In general, we have x n = n x m , i.e., the nth root of x, raised to the mth power. √ 1 (81) 2 = 81 = 9 , etc. Finally, we can dene negative exponents: x −n = x1n . Thus, x −1 = x1 , etc. Cont Examples 20 = 1, 23 = (2)(2)(2) = 8 (=3)4 = (=3) × (=3) × (=3) × (=3) = 81.Also, we can dene√fractional exponents in terms of roots, such as x 21 = x , the square root of x. √ √ 1 3 Similarly, x 3 = 3 x , the cube root of x , x 5 = 5 x 3 , etc. √ m In general, we have x n = n x m , i.e., the nth root of x, raised to the mth power. √ 1 (81) 2 = 81 = 9 , etc. Finally, we can dene negative exponents: x −n = x1n . Thus, x −1 = x1 , etc. Evaluating Functions To evaluate a function is to Replace (substitute) its variable with a given number or expression. Evaluate the function f (x ) = 2x + 4 for Just replace the variable ”x ” with ”5”: f (5) = 2 × 5 + 4 = 14 Answer: f (5) = 14 x =5 Evaluating Functions To evaluate a function is to Replace (substitute) its variable with a given number or expression. Evaluate the function f (x ) = 2x + 4 for Just replace the variable ”x ” with ”5”: f (5) = 2 × 5 + 4 = 14 Answer: f (5) = 14 x =5 Evaluating Functions To evaluate a function is to Replace (substitute) its variable with a given number or expression. Evaluate the function f (x ) = 2x + 4 for Just replace the variable ”x ” with ”5”: f (5) = 2 × 5 + 4 = 14 Answer: f (5) = 14 x =5 Evaluating Functions To evaluate a function is to Replace (substitute) its variable with a given number or expression. Evaluate the function f (x ) = 2x + 4 for Just replace the variable ”x ” with ”5”: f (5) = 2 × 5 + 4 = 14 Answer: f (5) = 14 x =5 Evaluating Functions To evaluate a function is to Replace (substitute) its variable with a given number or expression. Evaluate the function f (x ) = 2x + 4 for Just replace the variable ”x ” with ”5”: f (5) = 2 × 5 + 4 = 14 Answer: f (5) = 14 x =5 Cont Consider f (x ) = 1 − x + x 2 The "x" is just a place-holder(a dummy variable)! And ”f ” is just a name. It would be the same function if I wrote: f (q ) = 1 − q + q 2 w (A) = 1 − A + A2 h(j) = 1 − j + j2 Cont I) Let us evaluate that function f (x ) = 1 − x + x 2 for x = 3: f (3) = 1 − 3 + 32 =1−3+9 =7 Cont II) Let us evaluate the function f (x ) = 1 − x + x 2 for x = 1/r : f (1/r ) = 1 − (1/r ) + (1/r )2 III) Or evaluate the function for x = a − 4: f (a − 4) = 1 − (a − 4) + (a − 4)2 = 1 − a + 4 + a2 − 8a + 16 = 21 − 9a + a2 Constant Function Constant Function is a function of the form y = b, where b is a constant. It is also written as f(x) = b. The graph of a Constant Function is a horizontal line. The function f (x ) = 10 is constant since the values of f (x ) do not vary . Constant Function Constant Function is a function of the form y = b, where b is a constant. It is also written as f(x) = b. The graph of a Constant Function is a horizontal line. The function f (x ) = 10 is constant since the values of f (x ) do not vary . Constant Function Constant Function is a function of the form y = b, where b is a constant. It is also written as f(x) = b. The graph of a Constant Function is a horizontal line. The function f (x ) = 10 is constant since the values of f (x ) do not vary . Constant Function Constant Function is a function of the form y = b, where b is a constant. It is also written as f(x) = b. The graph of a Constant Function is a horizontal line. The function f (x ) = 10 is constant since the values of f (x ) do not vary . Limit and Continuity To say that limx →p f (x ) = L, means that (x) can be made as close as desired to L by making x close enough, but not equal, to p. of a constant function is the constant itself. Mathematically lim (c ) = c where c is a constant. Limit x →a Example 2 limx →3 xx −−11 = 32 −1 3−1 = 8 2 =4 Examples 2 nd limx →1 xx −−11 . Ans: Although the limit in question is the ratio of two polynomials, x = 1 makes both the numerator and denominator equal to zero. We need to factor both numerator and denominator as shown below. 2 x −1) limx →1 xx −−11 = limx →1 (x +(x1)( −1) = limx →1 (x + 1) =1+1 =2 example Evaluate lim a 2+a23a+4−3 . a→∞ Solution: Here substituting a = ∞ in both polynomial makes ∞ form which is meaningless. So we need to factor out a ∞ highest power of indeterminate from both polynomials as shown below. a3 (1+ 2 − 3 ) lim a32+a23a+24−3 = lim a3 (2+a 4 a)3 3 a→∞ 2 a→∞ a3 2 − 3 1+ ∞ ∞ = 2+ 4 ∞ = 1+2+0−0 0 = 21 f is said to be continuous at a point following conditions are satised. f (a) is dened lim f (x ) exists Function a if the x →a lim f (x ) = f (a) x →a Roughly speaking, a function is said to be continuous at a point if it does not have any breaks, gaps or holes point at that point. Graphs below are the examples of continuous functtion. What can be infered from the above graphs? f is said to be continuous at a point following conditions are satised. f (a) is dened lim f (x ) exists Function a if the x →a lim f (x ) = f (a) x →a Roughly speaking, a function is said to be continuous at a point if it does not have any breaks, gaps or holes point at that point. Graphs below are the examples of continuous functtion. What can be infered from the above graphs? f is said to be continuous at a point following conditions are satised. f (a) is dened lim f (x ) exists Function a if the x →a lim f (x ) = f (a) x →a Roughly speaking, a function is said to be continuous at a point if it does not have any breaks, gaps or holes point at that point. Graphs below are the examples of continuous functtion. What can be infered from the above graphs? f is said to be continuous at a point following conditions are satised. f (a) is dened lim f (x ) exists Function a if the x →a lim f (x ) = f (a) x →a Roughly speaking, a function is said to be continuous at a point if it does not have any breaks, gaps or holes point at that point. Graphs below are the examples of continuous functtion. What can be infered from the above graphs? f is said to be continuous at a point following conditions are satised. f (a) is dened lim f (x ) exists Function a if the x →a lim f (x ) = f (a) x →a Roughly speaking, a function is said to be continuous at a point if it does not have any breaks, gaps or holes point at that point. Graphs below are the examples of continuous functtion. What can be infered from the above graphs? example Is f (x ) = xx −−11 continuous at x = 1? 3 Solution. No! because f (1) = 11−−11 = 3 0 0 which is meaningless. Quiz or False? 1) If a function f is not dened at x = a then it is not continuous at x = a. 2) If f is a function such that lim f (x ) does not exist then f is x →a not continuous. True Intercepts of a straight line The x-intercept of a line is the point at which the line crosses the x axis. ( i.e. where the y value equals 0 ) x − intercept =(x , 0) The y-intercept of a line is the point at which the line crosses the y axis. ( i.e. where the x value equals 0 ) y − intercept =(0, y ) Intercepts of a straight line The x-intercept of a line is the point at which the line crosses the x axis. ( i.e. where the y value equals 0 ) x − intercept =(x , 0) The y-intercept of a line is the point at which the line crosses the y axis. ( i.e. where the x value equals 0 ) y − intercept =(0, y ) Example: Find the x and y intercepts of the equation 3x + 4y = 12. Solution To nd the x-intercept, set y = 0 and solve for x . 3x + 4(0) = 12 =⇒ 3x + 0 = 12 =⇒ 3x = 12 =⇒ x = 12/3 =⇒ x = 4 cont To nd the y-intercept, set x = 0 and solve for y . 3(0) + 4y = 12 =⇒ 0 + 4y = 12 =⇒ 4y = 12 =⇒ y = 12/4 =⇒ y = 3 Therefore, the x-intercept is (4, 0) and the y-intercept is (0, 3). Slope of a st. line The slope m of the straight line (x1 , y1 ) and (x2 , y2 ) is given by m = yx22 −−yx11 through the points = vertical rise (x1 6= x2 ) (Slope Formula) horizontal run As you go from left to right, Uphill = Positive Slope Downhill = Negative Slope And of course, no change in height means that the line has zero slope. Slope of a st. line The slope m of the straight line (x1 , y1 ) and (x2 , y2 ) is given by m = yx22 −−yx11 through the points = vertical rise (x1 6= x2 ) (Slope Formula) horizontal run As you go from left to right, Uphill = Positive Slope Downhill = Negative Slope And of course, no change in height means that the line has zero slope. Slope of a st. line The slope m of the straight line (x1 , y1 ) and (x2 , y2 ) is given by m = yx22 −−yx11 through the points = vertical rise (x1 6= x2 ) (Slope Formula) horizontal run As you go from left to right, Uphill = Positive Slope Downhill = Negative Slope And of course, no change in height means that the line has zero slope. graph of slopes Examples Find the slope of the line segment joining the points (1, −4) and (−4, 2). Solution: Label the points as x1 = 1, y1 = −4, x2 = −4, and y2 = 2. To nd the slope m of the line segment joining the points, use the slope formula : 4) m = 2−−(− 4−1 = 2−+54 = − 65 So, m = − 65 . Graph with positive and negative slopes Parallel Lines Parallel lines have the same slope and will never intersect. Parallel lines continue, literally, forever without touching (assuming that these lines are on the same plane). If two lines l1 and l2 with slope m1 and m2 respectively are parallel then m1 = m2 . Parallel Lines Parallel lines have the same slope and will never intersect. Parallel lines continue, literally, forever without touching (assuming that these lines are on the same plane). If two lines l1 and l2 with slope m1 and m2 respectively are parallel then m1 = m2 . Parallel Lines Parallel lines have the same slope and will never intersect. Parallel lines continue, literally, forever without touching (assuming that these lines are on the same plane). If two lines l1 and l2 with slope m1 and m2 respectively are parallel then m1 = m2 . Perpendicular lines Perpendicular lines intersect each other at 90 degree. slope of perpendicular lines are the negative reciprocals of each other If two lines l1 and l2 with slope m1 and m2 respectively are perpendicular to each other then m1 = − m12 . the Perpendicular lines Perpendicular lines intersect each other at 90 degree. slope of perpendicular lines are the negative reciprocals of each other If two lines l1 and l2 with slope m1 and m2 respectively are perpendicular to each other then m1 = − m12 . the Equation of a straight line If the equation of the line is given in the form y = mx + b (Slope intercept form) m is the slope and b is y-intercept This form of a line's equation is called the slope-intercept form, because b can be interpreted as the y -intercept of the line, the y-coordinate where the line intersects the y-axis. The slope of the line dened by the linear equation ax + by + c = 0 is: − ba . Equation of a straight line If the equation of the line is given in the form y = mx + b (Slope intercept form) m is the slope and b is y-intercept This form of a line's equation is called the slope-intercept form, because b can be interpreted as the y -intercept of the line, the y-coordinate where the line intersects the y-axis. The slope of the line dened by the linear equation ax + by + c = 0 is: − ba . Equation of a straight line If the equation of the line is given in the form y = mx + b (Slope intercept form) m is the slope and b is y-intercept This form of a line's equation is called the slope-intercept form, because b can be interpreted as the y -intercept of the line, the y-coordinate where the line intersects the y-axis. The slope of the line dened by the linear equation ax + by + c = 0 is: − ba . Equation of a straight line If the equation of the line is given in the form y = mx + b (Slope intercept form) m is the slope and b is y-intercept This form of a line's equation is called the slope-intercept form, because b can be interpreted as the y -intercept of the line, the y-coordinate where the line intersects the y-axis. The slope of the line dened by the linear equation ax + by + c = 0 is: − ba .