Download x 2 - CB East Wolf

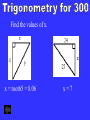
Jeopardy Math Review
Unit 1:
Functions and
Their Graphs
Unit 2:
Polynomial and
Rational
Functions
Unit 3:
Exponential and
Logarithmic
Functions
Unit 4:
Trigonometry
Unit 1:
Functions and
Their Graphs II
100
100
100
100
100
200
200
200
200
200
300
300
300
300
300
400
400
400
400
400
500
500
500
500
500
Final Jeopardy
Calculate the midpoint between the points:
(8, -5) and (-2, 3)
Calculate the distance between the points:
(-7, 4) and (1, 6)
Midpoint = (3, -1)
Distance = root68 = 8.25
Calculate the slope of the line through the
given points:
Line A: (2, 4) (-3, 5)
Slope = -1/5
Line B: (0, -7) (1, -2)
Slope = 5
What kind of lines are A and B?
perpendicular
Write the slope-intercept equation of the line
that meets the following criteria:
Line C: Parallel to the line y = 3x – 9 and
through the point (2, -2)
y = 3x - 8
Given the following pairs of points, write
the point-slope form of the line:
Line F: (1, 2) and (0, -5)
y - 2= 1/7(x – 1)
OR
y + 5 = 1/7(x – 0)
f-1(x) = x2 – 8
3
vertex = (-2, 6)
axis of symmetry: X = -2
x-intercept(s) = -5 and 1
y-intercept(s) = 4
max @ (-2, 6)
max/min =
equation of graph:
y = -(x + 2)2 + 6
Write the equation of the quadratic function
given the vertex and point.
Vertex = (4, 5)
Point = (3, 2)
y = -3(x – 4)2 + 5
Completely factor the polynomials:
-2x(x + 2)(x -1)
(3x - 1)(x + 2)
Use Synthetic Division to find the quotient.
x2 -2x +6
Write the complex number in standard form and
write its conjugate.
15 + 6i 15 – 6i
Find the sum.
Find the product.
18 – 3i
-27 + 23i
Write the complex fraction in standard form.
-2 + 29i
13
Solve the nonlinear inequality:
-2 < x < 7
Evaluate the exponential function:
f(2/3) = 0
Write the logarithm as an exponential:
361/2 = 6
Solve the equation for x:
x=5
Evaluate the logarithms:
-3
-3
1
Write the exponential as a logarithm:
log5(25) = 2
Solve the logarithmic equation for x:
x = -3
Using a calculator, evaluate the logarithm:
1.44
Expand the logarithmic equation:
= log(4y3 +2) – 6log(x) – 2 log(z)
Condense the logarithmic equation:
= log8[(z-5)2/(x+3)6]
Solve for x.
x = 32
x = 6.77
x = 100.86
Convert the radian measure to degrees:
330°
Convert the degree measure to radians:
5π/6
Find the supplement of the angle:
7π/4
Find the complement of the angle:
π/4
Evaluate the following:
Undefined
Root2/2
-root3/2
Find the values of x.
x = root65 = 8.06
x=7
Evaluate the trigonometric functions of the
angle.
5/root61
-6/root61
-5/6
-root10/10
-root10
3root10/10
root10/3
-1/3
-3
f(2) = 11
x = -1, 1
f(x + 3) = 5x2 + 30x + 36
x = all real numbers except -7
x = all real numbers greater than or equal to -12
f(x) is neither
Use bracket notation to describe all increasing,
decreasing, or constant intervals of the graph.
INC DEC
(-∞, -8] [-8, -5]
INC
[-5, 8)
DEC
(8, 6]
INC
[6, ∞)
Write the equation of the quadratic parent
function with A = -1, B = 5 and C = -3.
y = -(x+5)2 – 3
Describe the effects that each value (A, B,
and C) has on the graph of the quadratic
parent function.
A = -1 means the graph is flipped over the x-axis
B = 5 means the graph is shifted to the left 5 units
C = -3 means the graph is shifted down 3 units
f(x) + g(x) = x2 +x +1
f(x)•g(x) = 3x3 - 7x2 + 8x -2
f(g(x)) = 9x2 - 12x + 5
Unit 5:
Graphs and Inverses of
Trigonometric Functions
Fill in the table and write the equation that
the graph models.
amplitude = 3 period = π left endpoint = (0, 5) max = 5
a= 3
b= 2
c= 0
d= 2
y = 2 + 3cos(2x)