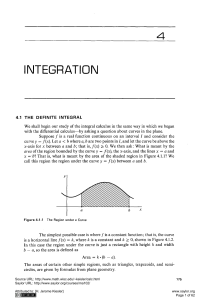
Section 4.1: The Definite Integral
... variable x. Thus when there are two or more variables we can tell dummy variable in an integral. For example, x 2 t can be integrated respect to either x or t. With respect to x, ...
... variable x. Thus when there are two or more variables we can tell dummy variable in an integral. For example, x 2 t can be integrated respect to either x or t. With respect to x, ...
4.6 Finding Antiderivatives
... Changing Variables with Definite Integrals If we need to change variables in a definite integral, we have two choices: • First work out the corresponding indefinite integral and then use that antiderivative and FTC2 to evaluate the definite integral. • Change variables in the definite integral, whic ...
... Changing Variables with Definite Integrals If we need to change variables in a definite integral, we have two choices: • First work out the corresponding indefinite integral and then use that antiderivative and FTC2 to evaluate the definite integral. • Change variables in the definite integral, whic ...
CENTRAL LIMIT THEOREMS AND QUADRATIC VARIATIONS IN
... given in (i) on one side, then of a quantity related to the Malliavin derivative on another side, so that one does not need to consider all moments as in the original proof of Breuer and Major. In a first subsection we recall the main tools in our framework in the classical context of stochastic int ...
... given in (i) on one side, then of a quantity related to the Malliavin derivative on another side, so that one does not need to consider all moments as in the original proof of Breuer and Major. In a first subsection we recall the main tools in our framework in the classical context of stochastic int ...
Homogenization Rate of Diffusive Tracers in Chaotic Advection
... In general, if f(x) is getting closer and closer to L as x gets closer and closer to a, we say that the limit of f(x) as x approaches a is L, written ...
... In general, if f(x) is getting closer and closer to L as x gets closer and closer to a, we say that the limit of f(x) as x approaches a is L, written ...
PDF (Chapter 7)
... integration formulas derived in Chapters 4-6. We then present the two most important general techniques: integration by substitution and integration by parts. As the techniques for evaluating integrals are developed, you will see that integration is a more subtle process than differentiation and tha ...
... integration formulas derived in Chapters 4-6. We then present the two most important general techniques: integration by substitution and integration by parts. As the techniques for evaluating integrals are developed, you will see that integration is a more subtle process than differentiation and tha ...
Notes on Calculus II Integral Calculus Miguel A. Lerma
... small amounts f (x) dx. The symbol dx was interpreted as the length of an “infinitesimal” interval, sort of what ∆x becomes for infinite n. This interpretation was later abandoned due to the difficulty of reasoning with infinitesimals, but we keep the notation. Remark : Note that in intervals where ...
... small amounts f (x) dx. The symbol dx was interpreted as the length of an “infinitesimal” interval, sort of what ∆x becomes for infinite n. This interpretation was later abandoned due to the difficulty of reasoning with infinitesimals, but we keep the notation. Remark : Note that in intervals where ...
Conditional expectation
... The final claim holds since every random variable is independent of the trivial σ-algebra. l Theorem 3.4. If G1 Ă G2 Ă F, then ErErX | G1 s | G2 s “ ErErX | G2 s | G1 s “ ErX | G1 s. Remark 3.5. In words, this says that in a battle between nested σ-algebras, the smallest ...
... The final claim holds since every random variable is independent of the trivial σ-algebra. l Theorem 3.4. If G1 Ă G2 Ă F, then ErErX | G1 s | G2 s “ ErErX | G2 s | G1 s “ ErX | G1 s. Remark 3.5. In words, this says that in a battle between nested σ-algebras, the smallest ...
Antiderivatives - John Abbott College
... (−6x−1 − 4x + 12) dx = −6 ln |x| − 2x2 + 12x + C2 replace x = 1 and f (1) = 9 to solve for C2 : 9 = −6 ln |1| − 2(1)2 + 12(1) + C2 =⇒ C2 = −1 Answer 2: f (x) = −6 ln |x| − 2x2 + 12x − 1 ...
... (−6x−1 − 4x + 12) dx = −6 ln |x| − 2x2 + 12x + C2 replace x = 1 and f (1) = 9 to solve for C2 : 9 = −6 ln |1| − 2(1)2 + 12(1) + C2 =⇒ C2 = −1 Answer 2: f (x) = −6 ln |x| − 2x2 + 12x − 1 ...
AP Calculus AB Course Outline
... the use of color. Students are expected to use proper vocabulary and terminology when giving verbal explanations to their fellow classmates, as well as to the instructor. Technology is also available through the use of a Texas Instruments TI-89 graphing calculator that can be viewed via an overhead ...
... the use of color. Students are expected to use proper vocabulary and terminology when giving verbal explanations to their fellow classmates, as well as to the instructor. Technology is also available through the use of a Texas Instruments TI-89 graphing calculator that can be viewed via an overhead ...
Indefinite Integrals Calculus
... that you have learned, particularly in the case of an increasing (or decreasing) function. Left-hand and Right-hand sums are frequently used in calculations of numerical integrals because it is easy to find the left and right endpoints of each interval, and much more difficult to find the max/min of ...
... that you have learned, particularly in the case of an increasing (or decreasing) function. Left-hand and Right-hand sums are frequently used in calculations of numerical integrals because it is easy to find the left and right endpoints of each interval, and much more difficult to find the max/min of ...
Limit worksheets - Canvas
... Instructor’s overview – 2 The problems used in the slides below are indicative what level we expect throughout the course. Instructors will want to supplement these with both easier and harder examples as class progress dictates. One goal in providing these templates is to help ensure a uniform lev ...
... Instructor’s overview – 2 The problems used in the slides below are indicative what level we expect throughout the course. Instructors will want to supplement these with both easier and harder examples as class progress dictates. One goal in providing these templates is to help ensure a uniform lev ...
... infinite hyper-reals with negative sign, and non-constant hyper-reals. 8. The hyper-reals are totally ordered, and aligned along a line: the Hyper-real Line. 9. That line includes the real numbers separated by the nonconstant hyper-reals. Each real number is the center of an interval of hyper-reals, ...
Math 20B. Lecture Examples. Section 10.3. Convergence of series
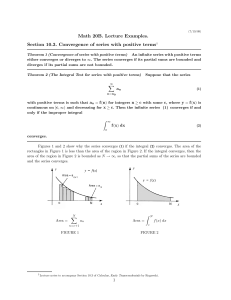
... Math 20B. Lecture Examples. Section 10.3. Convergence of series with positive terms† Theorem 1 (Convergence of series with positive terms) An infinite series with positive terms either converges or diverges to ∞. The series converges if its partial sums are bounded and diverges if its partial sums a ...
... Math 20B. Lecture Examples. Section 10.3. Convergence of series with positive terms† Theorem 1 (Convergence of series with positive terms) An infinite series with positive terms either converges or diverges to ∞. The series converges if its partial sums are bounded and diverges if its partial sums a ...
MATH_125_online_L5__..
... [00:00:00.12] Hello, everyone, and welcome back for Lecture 5. Today's lecture will focus on part two of the fundamental theorem of calculus, which, recall is in Section 5.3 of your textbook, and on a related result from Section 5.4, which is called the net change theorem. Let's start by recalling p ...
... [00:00:00.12] Hello, everyone, and welcome back for Lecture 5. Today's lecture will focus on part two of the fundamental theorem of calculus, which, recall is in Section 5.3 of your textbook, and on a related result from Section 5.4, which is called the net change theorem. Let's start by recalling p ...
Surface and Volume Integrals
... Note that if the current density J is uniformly radial over the curved surface, then so must be the electric field E, i.e. E = E r̂. Using Ohm’s law ...
... Note that if the current density J is uniformly radial over the curved surface, then so must be the electric field E, i.e. E = E r̂. Using Ohm’s law ...
Math 107H Topics for the first exam Integration Antiderivatives
... So, typically, using twice as many intervals (i.e., doing twice the work) gives us an estimate about 16 times closer to the real value of the integral. The importance of these estimates of the error is that they give us a means to decide beforehand how many subintervals to work with, in order to gua ...
... So, typically, using twice as many intervals (i.e., doing twice the work) gives us an estimate about 16 times closer to the real value of the integral. The importance of these estimates of the error is that they give us a means to decide beforehand how many subintervals to work with, in order to gua ...
this document - KSU Web Home
... In practice, …nding A using the de…nition is very di¢ cult. First, the expression resulting from the sum is usually very complicated. Then, we have to take its limit as n approaches in…nity. We will not spend any more time on it, but you should remember the formula. ...
... In practice, …nding A using the de…nition is very di¢ cult. First, the expression resulting from the sum is usually very complicated. Then, we have to take its limit as n approaches in…nity. We will not spend any more time on it, but you should remember the formula. ...
Calculus 7.1A lesson notes
... Area Between f(x) and x-axis The area between f (x) and the x axis can be found as follows: If f (x) is above the x axis: Area = ...
... Area Between f(x) and x-axis The area between f (x) and the x axis can be found as follows: If f (x) is above the x axis: Area = ...
Summer Calculus BC Homework
... still be expected to perform all of these (and other) algebra and trigonometry tasks that students saw in Pre-Calculus Honors. At the end of each item is a short statement for Calculus AB students, about where in Calculus we will see these skills. Power Reduction Formulas. Which of the following i ...
... still be expected to perform all of these (and other) algebra and trigonometry tasks that students saw in Pre-Calculus Honors. At the end of each item is a short statement for Calculus AB students, about where in Calculus we will see these skills. Power Reduction Formulas. Which of the following i ...
The Cartesian Plane and Functions - WBM
... • If degree of numerator < degree of denominator, then L = 0 • If degree of num = degree of denom, then L = ratio of leading coefficients • If degree of num > degree of denom, then L does not exist Calculus 3.5 ...
... • If degree of numerator < degree of denominator, then L = 0 • If degree of num = degree of denom, then L = ratio of leading coefficients • If degree of num > degree of denom, then L does not exist Calculus 3.5 ...
MATH 212
... Second Graded Assignment. Complete solutions required for full credit. Due: May 19. (Numbers in parentheses are from 8 th edition.) Page 359: 87 (Page 357: 73) Page 361: 151 (Page 357: 75) Page 404:10; 11; 13 (Page 402: 8; 9; 10) Project Assignment. Do one of the following. Solution must be in print ...
... Second Graded Assignment. Complete solutions required for full credit. Due: May 19. (Numbers in parentheses are from 8 th edition.) Page 359: 87 (Page 357: 73) Page 361: 151 (Page 357: 75) Page 404:10; 11; 13 (Page 402: 8; 9; 10) Project Assignment. Do one of the following. Solution must be in print ...
Math 131The Fundamental Theorem of Calculus (Part 2)
... Observe: Distance has been expressed as product, much the way we assumed earlier that the area of a rectangle could be expressed as a product: area of a rectangle = height ⇥ base. We can extend this analogy to Riemann sums and area under curves. While the velocity is not constant on long intervals s ...
... Observe: Distance has been expressed as product, much the way we assumed earlier that the area of a rectangle could be expressed as a product: area of a rectangle = height ⇥ base. We can extend this analogy to Riemann sums and area under curves. While the velocity is not constant on long intervals s ...
Section 3 Integral Equations
... has the 1 non-trivial linearly independent solution x1 = (1 − 1)T . If solutions do exist they will therefore have the form x = xP S + α1 x1 . A solution to the problem Ax = b will exist if x̂1 · b = 0. This condition does hold for b = (1 2)T and so the theorem predicts that a solution will exist. I ...
... has the 1 non-trivial linearly independent solution x1 = (1 − 1)T . If solutions do exist they will therefore have the form x = xP S + α1 x1 . A solution to the problem Ax = b will exist if x̂1 · b = 0. This condition does hold for b = (1 2)T and so the theorem predicts that a solution will exist. I ...
Lim.B.2
... integration. The definite integral of a function over an interval is a mathematical tool with many interpretations and applications involving accumulation. Antidifferentation is an underlying concept involved in solving separable differential equations. Solving separable differential equations invol ...
... integration. The definite integral of a function over an interval is a mathematical tool with many interpretations and applications involving accumulation. Antidifferentation is an underlying concept involved in solving separable differential equations. Solving separable differential equations invol ...