Download Lecture_9

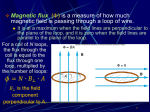
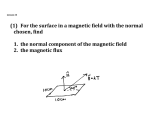
Chapter 28
Sources of Magnetic Field
Copyright © 2009 Pearson Education, Inc.
28-4 Ampère’s Law
Example 28-8: A nice use for Ampère’s law.
Use Ampère’s law to show that in any region of
space where there are no currents the
magnetic field cannot be both unidirectional
and nonuniform as shown in the figure.
Copyright © 2009 Pearson Education, Inc.
28-4 Ampère’s Law
Solving problems using Ampère’s law:
• Ampère’s law is only useful for solving
problems when there is a great deal of
symmetry. Identify the symmetry.
• Choose an integration path that reflects the
symmetry (typically, the path is along lines
where the field is constant and perpendicular
to the field where it is changing).
• Use the symmetry to determine the direction
of the field.
• Determine the enclosed current.
Copyright © 2009 Pearson Education, Inc.
28-5 Magnetic Field of a Solenoid
and a Toroid
A solenoid is a coil of wire containing
many loops. To find the field inside, we use
Ampère’s law along the path indicated in
the figure.
Copyright © 2009 Pearson Education, Inc.
28-5 Magnetic Field of a Solenoid
and a Toroid
The field is zero outside the solenoid,
and the path integral is zero along the
vertical lines, so the field is (n is the
number of loops per unit length)
Copyright © 2009 Pearson Education, Inc.
28-5 Magnetic Field of a Solenoid
and a Toroid
Example 28-9: Field inside a solenoid.
A thin 10-cm-long solenoid used for fast
electromechanical switching has a total of
400 turns of wire and carries a current of
2.0 A. Calculate the field inside near the
center.
Copyright © 2009 Pearson Education, Inc.
28-5 Magnetic Field of a Solenoid
and a Toroid
Example 28-10: Toroid.
Use Ampère’s law to
determine the magnetic
field (a) inside and (b)
outside a toroid, which is
like a solenoid bent into
the shape of a circle as
shown.
Copyright © 2009 Pearson Education, Inc.
28-6 Biot-Savart Law
The Biot-Savart law gives the magnetic
field due to an infinitesimal length of
current; the total field can then be found
by integrating over the total length of all
currents:
Copyright © 2009 Pearson Education, Inc.
28-6 Biot-Savart Law
Example 28-11: B due to current I in straight wire.
For the field near a long straight wire carrying a
current I, show that the Biot-Savart law gives
B = μ0I/2πR.
Copyright © 2009 Pearson Education, Inc.
28-6 Biot-Savart Law
Example 28-12: Current loop.
Determine B
B for points on the axis of a
circular loop of wire of radius R carrying a
current I.
Copyright © 2009 Pearson Education, Inc.
28-6 Biot-Savart Law
Example 28-13: B due to a wire segment.
One quarter of a circular loop of wire carries a
current I. The current I enters and leaves on
straight segments of wire, as shown; the straight
wires are along the radial direction from the center
C of the circular portion. Find the magnetic field at
point C.
Copyright © 2009 Pearson Education, Inc.
28-7 Magnetic Materials –
Ferromagnetism
Ferromagnetic materials are those that
can become strongly magnetized, such as
iron and nickel.
These materials are made up of tiny
regions called domains; the magnetic field
in each domain is in a single direction.
Copyright © 2009 Pearson Education, Inc.
28-7 Magnetic Materials –
Ferromagnetism
When the material is
unmagnetized, the
domains are randomly
oriented. They can be
partially or fully aligned
by placing the material
in an external magnetic
field.
Copyright © 2009 Pearson Education, Inc.
28-7 Magnetic Materials –
Ferromagnetism
A magnet, if undisturbed, will tend to retain its
magnetism. It can be demagnetized by shock or
heat.
The relationship between the external magnetic
field and the internal field in a ferromagnet is
not simple, as the magnetization can vary.
Copyright © 2009 Pearson Education, Inc.
ConcepTest 28.3 Current Loop
1) left
What is the direction of the
2) right
magnetic field at the center
3) zero
(point P) of the square loop
4) into the page
of current?
5) out of the page
I
P
ConcepTest 28.3 Current Loop
1) left
What is the direction of the
magnetic field at the center
(point P) of the square loop
of current?
2) right
3) zero
4) into the page
5) out of the page
Use the right-hand rule for each
wire segment to find that each
segment has its B field pointing
out of the page at point P.
I
P
28-8 Electromagnets and Solenoids –
Applications
Remember that a solenoid is a long coil of
wire. If it is tightly wrapped, the magnetic field
in its interior is almost uniform.
Copyright © 2009 Pearson Education, Inc.
28-9 Magnetic Fields in Magnetic
Materials; Hysteresis
If a ferromagnetic material is placed in the core
of a solenoid or toroid, the magnetic field is
enhanced by the field created by the
ferromagnet itself. This is usually much greater
than the field created by the current alone.
If we write
B = μI
where μ is the magnetic permeability,
ferromagnets have μ >> μ0, while all other
materials have μ ≈ μ0.
Copyright © 2009 Pearson Education, Inc.
28-9 Magnetic Fields in Magnetic
Materials; Hysteresis
Not only is the
permeability very large
for ferromagnets, its
value depends on the
external field.
Copyright © 2009 Pearson Education, Inc.
28-9 Magnetic Fields in Magnetic
Materials; Hysteresis
Furthermore, the induced
field depends on the history
of the material. Starting
with unmagnetized material
and no magnetic field, the
magnetic field can be
increased, decreased,
reversed, and the cycle
repeated. The resulting plot
of the total magnetic field
within the ferromagnet is
called a hysteresis loop.
Copyright © 2009 Pearson Education, Inc.
28-10 Paramagnetism and Diamagnetism
All materials exhibit some level of magnetic
behavior; most are either paramagnetic (μ
slightly greater than μ0) or diamagnetic (μ
slightly less than μ0). The following is a table
of magnetic susceptibility χm, where
χm = μ/μ0 – 1.
Copyright © 2009 Pearson Education, Inc.
28-10 Paramagnetism and Diamagnetism
Molecules of paramagnetic materials have a
small intrinsic magnetic dipole moment, and
they tend to align somewhat with an external
magnetic field, increasing it slightly.
Molecules of diamagnetic materials have no
intrinsic magnetic dipole moment; an
external field induces a small dipole moment,
but in such a way that the total field is
slightly decreased.
Copyright © 2009 Pearson Education, Inc.
Summary of Chapter 28
• Magnitude of the field of a long, straight
current-carrying wire:
• The force of one current-carrying wire on
another defines the ampere.
• Ampère’s law:
Copyright © 2009 Pearson Education, Inc.
Summary of Chapter 28
• Magnetic field inside a solenoid:
• Biot-Savart law:
• Ferromagnetic materials can be made
into strong permanent magnets.
Copyright © 2009 Pearson Education, Inc.
Chapter 29
Electromagnetic Induction
and Faraday’s Law
Copyright © 2009 Pearson Education, Inc.
Units of Chapter 29
• Induced EMF
• Faraday’s Law of Induction; Lenz’s Law
• EMF Induced in a Moving Conductor
• Electric Generators
• Back EMF and Counter Torque; Eddy
Currents
Copyright © 2009 Pearson Education, Inc.
Units of Chapter 29
• Transformers and Transmission of
Power
• A Changing Magnetic Flux Produces an
Electric Field
• Applications of Induction: Sound
Systems, Computer Memory,
Seismograph, GFCI
Copyright © 2009 Pearson Education, Inc.
29-1 Induced EMF
Almost 200 years ago, Faraday looked for
evidence that a magnetic field would induce
an electric current with this apparatus:
Copyright © 2009 Pearson Education, Inc.
29-1 Induced EMF
He found no evidence when the current was
steady, but did see a current induced when the
switch was turned on or off.
Copyright © 2009 Pearson Education, Inc.
ConcepTest 29.1 Magnetic Flux I
In order to change the
magnetic flux through
the loop, what would
you have to do?
1) drop the magnet
2) move the magnet upward
3) move the magnet sideways
4) only (1) and (2)
5) all of the above
ConcepTest 29.1 Magnetic Flux I
In order to change the
magnetic flux through
the loop, what would
you have to do?
1) drop the magnet
2) move the magnet upward
3) move the magnet sideways
4) only (1) and (2)
5) all of the above
Moving the magnet in any direction would
change the magnetic field through the
loop and thus the magnetic flux.
29-1 Induced EMF
Therefore, a changing magnetic field induces
an emf.
Faraday’s experiment used a magnetic field
that was changing because the current
producing it was changing; the previous
graphic shows a magnetic field that is
changing because the magnet is moving.
Copyright © 2009 Pearson Education, Inc.
29-2 Faraday’s Law of Induction;
Lenz’s Law
The induced emf in a wire loop is proportional
to the rate of change of magnetic flux through
the loop.
Magnetic flux:
Unit of magnetic flux: weber, Wb:
1 Wb = 1 T·m2.
Copyright © 2009 Pearson Education, Inc.
29-2 Faraday’s Law of Induction;
Lenz’s Law
This drawing shows the variables in the flux
equation:
Copyright © 2009 Pearson Education, Inc.
29-2 Faraday’s Law of Induction;
Lenz’s Law
The magnetic flux is analogous to the electric
flux – it is proportional to the total number of
magnetic field lines passing through the loop.
Copyright © 2009 Pearson Education, Inc.
29-2 Faraday’s Law of Induction;
Lenz’s Law
Conceptual Example 29-1: Determining flux.
A square loop of wire encloses area A1. A uniform
magnetic field B perpendicular to the loop
extends over the area A2. What is the magnetic
flux through the loop A1?
Copyright © 2009 Pearson Education, Inc.
29-2 Faraday’s Law of Induction;
Lenz’s Law
Faraday’s law of induction: the emf induced in
a circuit is equal to the rate of change of
magnetic flux through the circuit:
or
dB
d
d


Note:   N
 N  A  B   N  A B cos  
dt
dt
dt
 

Copyright © 2009 Pearson Education, Inc.
29-2 Faraday’s Law of Induction;
Lenz’s Law
Example 29-2: A loop of wire in a magnetic
field.
A square loop of wire of side l = 5.0 cm is in a
uniform magnetic field B = 0.16 T. What is the
magnetic flux in the loop (a) when B is
perpendicular to the face of the loop and (b)
when B is at an angle of 30° to the area A of the
loop? (c) What is the magnitude of the average
current in the loop if it has a resistance of
0.012 Ω and it is rotated from position (b) to
position (a) in 0.14 s?
Copyright © 2009 Pearson Education, Inc.
29-2 Faraday’s Law of Induction;
Lenz’s Law
The minus sign gives the direction of the
induced emf:
A current produced by an induced emf moves in a
direction so that the magnetic field it produces tends to
restore the changed field.
or:
An induced emf is always in a direction that opposes
the original change in flux that caused it.
Copyright © 2009 Pearson Education, Inc.
29-2 Faraday’s Law of Induction;
Lenz’s Law
Magnetic flux will change if the area of the
loop changes.
Copyright © 2009 Pearson Education, Inc.
29-2 Faraday’s Law of Induction;
Lenz’s Law
Magnetic flux will change if the angle between
the loop and the field changes.
Copyright © 2009 Pearson Education, Inc.
29-2 Faraday’s Law of Induction;
Lenz’s Law
Conceptual Example 29-3: Induction stove.
In an induction stove, an ac current exists in
a coil that is the “burner” (a burner that
never gets hot). Why will it heat a metal pan
but not a glass container?
Copyright © 2009 Pearson Education, Inc.
29-2 Faraday’s Law of Induction;
Lenz’s Law
Problem Solving: Lenz’s Law
1. Determine whether the magnetic flux is increasing,
decreasing, or unchanged.
2. The magnetic field due to the induced current
points in the opposite direction to the original field
if the flux is increasing; in the same direction if it is
decreasing; and is zero if the flux is not changing.
3. Use the right-hand rule to determine the direction
of the current.
4. Remember that the external field and the field due
to the induced current are different.
Copyright © 2009 Pearson Education, Inc.
29-2 Faraday’s Law of Induction;
Lenz’s Law
Conceptual Example 29-4: Practice with
Lenz’s law.
In which direction is the current induced in
the circular loop for each situation?
Copyright © 2009 Pearson Education, Inc.
29-2 Faraday’s Law of Induction;
Lenz’s Law
Example 29-5: Pulling a coil from
a magnetic field.
A 100-loop square coil of wire, with side
l = 5.00 cm and total resistance 100 Ω, is
positioned perpendicular to a uniform
0.600-T magnetic field. It is quickly
pulled from the field at constant speed
(moving perpendicular to B
B) to a region
where B drops abruptly to zero. At t = 0,
the right edge of the coil is at the edge
of the field. It takes 0.100 s for the whole
coil to reach the field-free region. Find
(a) the rate of change in flux through the
coil, and (b) the emf and current
induced. (c) How much energy is
dissipated in the coil? (d) What was the
average force required (Fext)?
Copyright © 2009 Pearson Education, Inc.
ConcepTest 29.3 Moving Wire Loop I
A wire loop is being pulled
through a uniform magnetic
field. What is the direction
1) clockwise
2) counterclockwise
3) no induced current
of the induced current?
x x x x x x x x x x x x
x x x x x x x x x x x x
x x x x x x x x x x x x
x x x x x x x x x x x x
x x x x x x x x x x x x
x x x x x x x x x x x x
x x x x x x x x x x x x
ConcepTest 29.3 Moving Wire Loop I
A wire loop is being pulled
through a uniform magnetic
field. What is the direction
1) clockwise
2) counterclockwise
3) no induced current
of the induced current?
x x x x x x x x x x x x
x x x x x x x x x x x x
Since the magnetic field is uniform, the
x x x x x x x x x x x x
magnetic flux through the loop is not
x x x x x x x x x x x x
changing. Thus no current is induced.
x x x x x x x x x x x x
x x x x x x x x x x x x
x x x x x x x x x x x x
Follow-up: What happens if the loop moves out of the page?
ConcepTest 29.3 Moving Wire Loop II
A wire loop is being pulled
through a uniform magnetic
field that suddenly ends.
What is the direction of the
induced current?
x x x x x
x x x x x
x x x x x
x x x x x
x x x x x
x x x x x
x x x x x
1) clockwise
2) counterclockwise
3) no induced current
ConcepTest 29.3 Moving Wire Loop II
A wire loop is being pulled
through a uniform magnetic
field that suddenly ends.
What is the direction of the
1) clockwise
2) counterclockwise
3) no induced current
induced current?
x x x x x
The B field into the page is disappearing in
x x x x x
the loop, so it must be compensated by an
x x x x x
induced flux also into the page. This can
x x x x x
be accomplished by an induced current in
x x x x x
the clockwise direction in the wire loop.
x x x x x
x x x x x
Follow-up: What happens when the loop is completely out of the field?
HW # 9
Chapter 28 – 28, 31, 37
Chapter 29 – 6, 18
Copyright © 2009 Pearson Education, Inc.