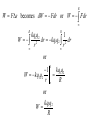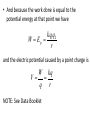Download Topic 9.3 Electric Field, Potential, and Energy

Topic 9.3 Electric Field, Potential,
and Energy
(2 hours)
Recall the definition of
Electric Potential
• We define the electric potential (V) at a point as
the work per unit charge that must be done to
bring a small positive test charge from far away to
the point of interest.
W
V
q
where V is the potential in volts (1 V = 1 J/C), W is
the work done (in J) which equals the potential
energy, and q is the magnitude of the test charge
(in C).
Charges and Potential Energy
• How much work must be done to bring in that
small positive test charge from infinity?
10
F (N)
9
8
7
6
5
4
3
2
1
q1
q2
r (m)
1
2
3
q2
4
R
W  Fs becomes dW   Fdr or W    Fdr

R
R
kq1q2
1
W    2 dr   kq1q2  2 dr
r
r


or
1
kq1q2
W   kq1q2

r 
R
R
or
kq1q2
W
R
• And because the work done is equal to the
potential energy at that point we have
kq1q2
W  Ep 
r
and the electric potential caused by a point charge is
W kq
V

q
r
NOTE: See Data Booklet
Example:
• Determine the electric potential on the
surface of a gold nucleus that has a radius of
6.2 fm.
Electric Potential Energy
and Electric Potential
• Note that electric potential energy and
electric potential are scalar quantities (they
can be positive or negative, but they have no
direction).
Example: Find the electric potential energy for
four charges (2.0 mC, 3.0 mC, 4.0 mC, 5.0 mC)
placed at the vertices of a square of side 10.0
cm. Now find the electric potential at the
center of the square.
Electric Field and Electric Potential
• Consider the movement of a small positive
test charge q in a uniform electric field as
shown below.
Electric Field and Electric Potential
• Suppose again that the charge +q is moved a small
distance by a force F from A to B so that the force
can be considered constant. The work done is given
by: ΔW = F Δx
Electric Field and Electric Potential
• The force F and the electric field E are oppositely
directed, and we know that:
F = -qE and ΔW = q ΔV = F Δx
• Therefore, the work done can be given as:
q ΔV = -q E Δx
• Therefore
V
E
x
Electric field is the negative gradient of potential.
Example:
• Determine how far apart two parallel plates
must be situated so that a potential difference
of 150. V produces an electric field strength of
1.00 × 103 NC-1.
Electric Field and Electric Potential of a
Charged Sphere of Radius r0
•Outside the sphere, the graphs
are the same as those of a point
charge.
•At the surface, r = r0. Therefore,
field and potential are at their
maximum values.
•Inside the sphere, the electric
field is zero.
•Inside the sphere, no work is done
to move a charge from a point
inside to the surface. Therefore,
there is no potential difference and
the potential is the same as it is
when r = r0.
Equipotentials
• Regions in space where the electric
potential of a charge distribution has
a constant value are called
equipotentials. The places where the
potential is constant in three
dimensions are called equipotential
surfaces, and where they are
constant in two dimensions they are
called equipotential lines.
• They are in some ways analogous to
the contour lines on topographic
maps where the gravitational
potential energy is constant as a
mass moves around the contour line
because the mass remains at the
same elevation above the Earth’s
surface. The gravitational field
strength acts in a direction
perpendicular to a contour line.
Field Lines and Equipotentials
• Similarly, because the electric potential on an
equipotential line has the same value, no work
can be done by an electric force when a test
charge moves on an equipotential. Therefore, the
electric field cannot have a component along an
equipotential, and thus the electric field must be
everywhere perpendicular to the equipotential
surface or equipotential line. This fact makes it
easy to plot equipotentials if the lines of force or
electric field lines are known.
Field Lines and Equipotentials
• NOTE: All points on the surface of a charged
conductor are at the same potential. That is, its
surface is an equipotential surface.
Example:
• Two spheres of radii r and R = 10r are
connected by a long conducting wire. Before
connecting, the big sphere had an amount of
charge Q on it and the smaller sphere was
uncharged. How much charge is there on
each sphere now?