Download Lecture XVII

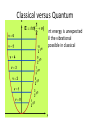
Classical Harmonic Oscillator
Let us consider a particle of mass ‘m’ attached to a spring
At the beginning at t = o the particle is at equilibrium, that is no force is working at it ,
F=0
In general, according to Hooke’s Law:
F = -k x
i.e. the force proportional to displacement and pointing in opposite direction and where k is
the force constant and x is the displacement.
Classically, a harmonic oscillator is subject to Hooke's law.
Newton's second law says
F = ma
Therefore,
d2 x
- k x =m 2 .
dt
d2 x
m 2 +k x=0.
dt
The solution to this differential equation is of the form:
x(t )  A sin( wt )
where the angular frequency of oscillation is ‘ω’ in radians per second
Also,
ω = 2πʋ,
where ‘ʋ’ is frequency of oscillation
Potential Energy
1 2 1 2
2
dU


Fdx

kx

kA
sin
wt


2
2
The parabolic potential energy V = ½ kx2 of a harmonic oscillator, where x is the
displacement from equilibrium.
The narrowness of the curve depends on the force constant k: the larger the value of k, the
narrower the well.
Kinetic energy
x  A sin wt
dx
 Aw cos wt
dt
1 2 1
K .E.  mv  mA2 w 2 cos 2 wt
2
2
Energy in Classical oscillator
E = T + V = ½ kA2 …….. How ????
Total energy is constant i.e. harmonic oscillator is a conservative system
Quantum Harmonic Oscillator
In classical physics, the Hamiltonian for a harmonic oscillator is given by:
where μ denotes the reduced mass:
The quantum mechanical harmonic oscillator is obtained by replacing the classical
position and momentum by the corresponding quantum mechanical operators.
Solution of Schrӧdinger Equation for Quantum Harmonic Oscillator
It is only possible if
Electromagnetic Spectrum
Near Infrared
Thermal Infrared
IR Stretching Frequencies of two bonded atoms:
What Does the Frequency, , Depend On?
E  h clas
h

2
k

 = frequency
k = spring strength (bond stiffness)
 = reduced mass (~ mass of largest atom)
 is directly proportional to the strength of the bonding between
the two atoms (  k)
 is inversely proportional to the reduced mass of the two atoms (v  1/)
51
Stretching Frequencies
• Frequency decreases with increasing atomic weight.
• Frequency increases with increasing bond energy.
52
IR spectroscopy is an important tool
in structural determination of
unknown compound
IR Spectra: Functional Grps
Alkane
-C-H
C-C
Alkene
Alkyne
15
IR: Aromatic Compounds
(Subsituted benzene “teeth”)
C≡C
16
IR: Alcohols and Amines
O-H broadens with Hydrogen bonding
CH3CH2OH
C-O
Amines similar to OH
N-H broadens with Hydrogen bonding
17
Question: A strong absorption band of infrared radiation is
observed for 1H35Cl at 2991 cm-1. (a) Calculate the force
constant, k, for this molecule. (b) By what factor do you
expect the frequency to shift if H is replaced by D? Assume
the force constant to be unaffected by this substitution.
[516.3 Nm-1; 0.717]
Hermite polynomial
• Recurrence Relation: A
Hermite Polynomial at
one point can be
expressed by
neighboring Hermite
Polynomials at the
same point.
H n x    1 e
n
x2

dn
2
exp

x
dx n

H n 1 x   2 xH n x   2nH n 1 x 
Quantum Mechanical Linear Harmonic Oscillator
1/ 2

 
 n  x    n

 2 n!  
e x
2
/2


Hn x 
It is interesting to calculate probabilities Pn(x) for finding a
harmonically oscillating particle with energy En at x; it is easier
to work with the coordinate q; for n=0 we have:
1/ 2
 1 
 0  q   A0 

  
e q
2
/2
1/ 2
 2 
 1  q   A1 

  
qe
1/ 2
 1 
 2  q   A2 

2  
1/ 2
 1 
 3  q   A3 

3  
 q2 / 2
 2q
 2q
2
3
 P0  q    0  q  
1
 P1  q    1  q  
2q 2
2
2
 1 e  q
2
/2
 3q  e  q
2


e q
eq
 P2  q    2  q 
/2
2
2
 P3  q    3  q 
2
 2q

 1
2
2 
2
 2q

3
2
e q
 3q 
3 
2
2
eq
2
Wave functions of the harmonic oscillator
Potential well, wave functions and probabilities
Energy levels are equally spaced with
separation of hʋ
Energy of ground state is not zero,
unlike in case of classical harmonic
oscillator
Energy of ground state is called zero
point energy

E0 = hʋ/2
Zero point energy is in accordance with
Heisenberg uncertainty principle
Show harmonic oscillator
eigenfunctions obey the
uncertainty principle ????
Difference from particle in a box
• P.E. varies in a parabolic manner with displacement from
the equilibrium and therefore wall of the “box” is not
vertical.
• In comparison to the “hard” vertical walls for a particle in
a box, walls are soft for harmonic oscillator.
Difference from particle in a box
• Spacing between allowed energy levels for the harmonic
oscillator is constant, whereas for the particle in a box,
the spacing between levels rises as the quantum number
increases.
• v=0 is possible since E will not be zero.
Classical versus Quantum
• The lowest allowed zero-point energy is unexpected
on classical grounds, since all the vibrational
energies, down to zero, are possible in classical
oscillator case.
Classical versus Quantum
• In quantum harmonic oscillator, wavefunction has
maximum in probability at x = 0. Contrast bahaviour
with the classic harmonic oscillator, which has a
minimum in the probability at x = 0 and maxima at
turning points.
Classical versus Quantum
• Limits of oscillation are strictly obeyed for the classical
oscillator. In contrast, the probability density for the
quantum oscillator leaks out beyond the classical limit.
Classical versus Quantum
• The probability density for quantum oscillator have n+1
peaks and n minima. This means that for a particular
quantum state n, there will be exactly n forbidden
location where wavefunction goes to zero. This is very
different from the classical case, where the mass can be
at any location within the limit.
Classical versus Quantum
• At high v, probability of
observing the oscillator is
greater near the turning
points than in the middle.
• At very large v (= 20), gaps
between the peaks in the
probability density becomes
very small. At large
energies, the distance
between the peaks will be
smaller than the Heisenberg
uncertainty principle allows
for observation.
Classical versus Quantum
• The region for non-zero
probability outside classical
limits drops very quickly for
high energies, so that this
region will be unobservable as
a result of the uncertainty
principle. Thus, the quantum
harmonic oscillator smoothly
crosses over to become
classical oscillator. This
crossing over from quantum to
classical behaviour was called
“Correspondence Principle” by
Bohr.
∆x ∆p=ħ/2