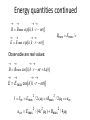Download Maxwell`s equations

Maxwell’s equations
Dr. Alexandre Kolomenski
Maxwell
(13 June 1831 – 5 November 1879) was a
Scottish physicist.
Famous equations published in 1861
Maxwell’s equations: integral form
Gauss's
law
Gauss's law for magnetism:
no magnetic monopole!
Ampère's law
(with Maxwell's addition)
Faraday's law of induction
(Maxwell–Faraday equation)
Relation of the speed of light and electric
and magnetic vacuum constants
ε0
permittivity of free space, also
called the electric constant
As/Vm or F/m (farad per
meter)
μ0
permeability of free space, also
called the magnetic constant
Vs/Am or H/m (henry per
meter)
Differential operators



t
Ax Ay Az


the divergence operator   A 
x
y
z
div
the curl operator
curl, rot
xˆ


 A 
x
Ax
yˆ

y
Ay
zˆ

z
Az
Other notation used
x 
the partial derivative with respect to time

x
Transition from integral to
differential form
Gauss’ theorem for a vector field F(r)
Volume V, surrounded by surface S
Stokes' theorem for a vector field
F(r)
Surface , surrounded by contour 
Maxwell’s equations: integral form
Gauss's law
Gauss's law for magnetism:
no magnetic monopoles!
Ampère's law
(with Maxwell's addition)
Maxwell–Faraday equation
(Faraday's law of induction)
Maxwell’s equations (SI units)
differential form
 density of charges
j density of current
Electric and magnetic fields and units
E
electric field,
volt per meter, V/m
B
the magnetic field
or magnetic induction
tesla, T
D
electric displacement
field
coulombs per square meter,
C/m^2
H
magnetic field
ampere per meter, A/m
Constitutive relations
These equations specify the response of bound charge and current to the
applied fields and are called constitutive relations.
P is the polarization field,
M is the magnetization field, then
where ε is the permittivity and μ the permeability of the material
.
Wave equation
0



2

2

  (  B )  (  B )   B   B
2


 


1  
1 2 B
  ( E )  (  E )  (  2
B)   2
t
t
t
c t
c t 2
Double vector product rule is used
a x b x c = (ac) b - (ab) c

2

1  B
 B 2
0
2
c t

2

1  E
2 E  2
0
2
c t
,
)
2 more differential operators
2
2 or  Laplace operator or Laplacian

A

d'Alembert operator or d'Alembertian
=
2
 Ax
 2 Ay
 2 Az


x 2
y 2
z 2
Plane waves
Thus, we seek the
solutions of the form:


 


 
B  B 0 Exp[i ( k  r  t )]
E  E 0 Exp[i( k  r  t )]


From Maxwell’s equations
one can see that

 
 B  i k  B


E
B

k

is parallel to E

 E  i k  E
is parallel to
B
Energy transfer and Pointing vector
Differential form of Pointing theorem
u is the density of electromagnetic energy of the field
||
S is directed along the propagation


direction
E
H

Integral form of Pointing theorem
k
Energy quantities continued


 
B  B max exp[i ( k  r  t )]


 
E  E max exp[i ( k  r  t )]
Bmax  Emax / c
Observable are real values:




 
B  B max cos[i ( k  r  t   )]
 
E  E max cos[i ( k  r  t )]
I  Sav  Emax 2 / 2c0  cBmax 2 / 2 0  cuav
uav  Emax 2 / (4c 2 0 )  Bmax 2 / 4 0